3.7 Conditioning Possibility Measures

There are two approaches given in the literature for defining conditional possibility measures. The first takes the view of a possibility measure as a special case of a plausibility function and applies DS conditioning. Recall that Plaus(V || U) = Plaus(V ∩ U)/ Plaus(V); similarly, define Poss(V || U) = Poss(V ∩ U)/ Poss(U). It is easy to check that Poss( || U) defined in this way is indeed a possibility measure (Exercise 3.21).

This definition, however, is not the one usually considered in the literature. The more common definition of conditional possibility takes as its point of departure the fact that min should play the same role in the context of possibility as multiplication does for probability. In the case of probability, this role is characterized by CP3. With this in mind, I take a conditional possibility measure Poss to be a function mapping a Popper algebra 2^W ′ to [0, 1], satisfying the following four properties:

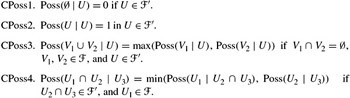
CPoss4 is just the result of replacing μ by Poss and by min in CP3.

Proposition 3.2.1 (and some of the subsequent discussion) shows that, given an unconditional probability measure μ defined on an algebra , the conditional probability measure μ^c defined by taking μ^c(V | U) = μ(V ∩ U)/μ(U) is the unique conditional probability measure defined on ′, where ′ = {U : μ(U) > 0}, satisfying CP1–3. The analogue of this observation does not hold for possibility. For example, consider the unconditional possibility measure Poss on W ={w₁, w₂, w₃} such that Poss(w₁) = 2/3, Poss(w₂) = 1/2, and Poss(w₃) = 1. Let U = {w₁, w₂} and V = {w₁}. Then, for all α ∈ [2/3, 1], there is a conditional possibility measure Poss_α on W that is an extension of Poss (i.e., Poss_α|W = Poss) and satisfies CPoss1–4 such that Poss(V | U) = α (Exercise 3.22).

One approach that has been taken in the literature to defining a canonical conditional possibility measure determined by an unconditional possibility measure is to make things "as possible as possible." That is, given an unconditional possibility measure Poss, the largest conditional possibility measure Poss′ consistent with CPoss1–4 that is an extension of Poss is considered. This leads to the following definition in the case that Poss(U) > 0:

I leave it to the reader to check that the conditional possibility measure defined in this way satisfies CPoss1–4 and, in fact, it is in a precise sense the largest conditional possibility measure that is an extension of Poss and CPoss1–4 (Exercise 3.23). With this definition, there is no direct analogue to Bayes' Rule; Poss(V | U) is not determined by Poss(U | V), Poss(U), and Poss(V) (Exercise 3.24). However, it is immediate from CPoss4 that there is still a close relationship among Poss(V | U), Poss(U | V), Poss(U), and Poss(V) that is somewhat akin to Bayes' Rule, namely,