3.5 Conditioning Inner and Outer Measures

How should conditioning be done for inner and outer measures? More precisely, suppose that μ is a probability measure defined on a subalgebra ′ of . What should μ_*(V | U) and μ*(V | U) be if U, V ∊ ? The first thought might be to take the obvious analogue of the definitions of μ_*(V) and μ*(V), and define, for example, μ*(V | U) to be min{μ(V′|U′): U′⊇U, V′⊇V, U′, V′ ∊ ′}. However, this definition is easily seen to be quite unreasonable. For example, if U and V are in ′, it may not give μ(V | U). For example, suppose that V ⊆ U, V ∊ , and μ(V) < μ(U) < 1. Taking V ′ = V and U′ = W, it follows from this definition that μ*(V | U) ≤ μ(V). Since μ(V) < μ(V | U), this means that μ*(V | U) < μ(V | U). This certainly doesn't seem reasonable.

One way of fixing this might be to take U′ to be a subset of U in the definition of μ*, that is, taking μ*(V | U) to be min{μ(V′|U′) : U′ ⊆ U, V′ ⊇ V, U′, V′ ∊ ′}. But this choice also has problems. For example, if V ⊆ U, U, V ∊ ′, and μ(U − V) > 0, then according to this definition, μ*(V | U) ≤ μ(V | U − V) = 0. Again, this does not seem right.

The actual definition is motivated by Theorem 2.3.3. Given a measure μ on ′, let _μ consist of all the extensions of μ to . Then for U, V ∊ such that μ*(U) > 0, define

Are there expressions for μ_*(V | U) and μ*(V | U) in terms of expressions such as μ_*(V ∩ U), μ*(U), analogous to the standard expression when all sets are measurable? One might guess that μ_*(V | U) = μ_*(V ∩ U)/μ*(U), taking the best approximation from below for the numerator and the best approximation from above for the denominator. This does not quite work. For suppose that μ_*(U) < μ*(U). Then μ_*(U)/μ*(U) < 1, while it is immediate that μ_*(U | U) = 1.

Although this choice gives inappropriate answers, something similar does much better. The idea for μ_*(V | U) is to have μ_*(V ∩ U) in the numerator, as expected. For the denominator, instead of using μ*(U), the set U is partitioned into V ∩ U and V ∩ U. For V ∩ U, the inner measure is used, since this is the choice made in the numerator. It is only for V ∩ U that the outer measure is used.

Theorem 3.5.1

Suppose that μ*(U) > 0. Then

Proof I consider μ_*(V | U) here. The argument for μ*(V | U) is almost identical and is left to the reader (Exercise 3.13). First, suppose that μ*(V ∩ U) = 0. Then it should be clear that μ′(V ∩ U) = 0, and so μ′(U) = μ′(V ∩ U), for all μ′ ∊ _μ. Thus μ′(V | U) = 1 for all μ′ ∊ _μ with μ′(U) > 0, and so μ_*(V | U) = 1. (This is true even if μ_*(V ∩ U) = 0.)

To show that (3.4) works if μ*(V ∩ U) > 0, I first show that if μ′ is an extension of μ to such that μ(U) > 0, then

By Theorem 2.3.3, μ_*(V ∩ U) ≤ μ′(V ∩ U) and μ′(V ∩ U) ≤ μ*(V ∩ U). By additivity, it follows that

In general, if x + y > 0, y ≥ 0, and x ≤ x′, then x/(x + y) ≤ x′/(x′ + y) (Exercise 3.13). Thus,

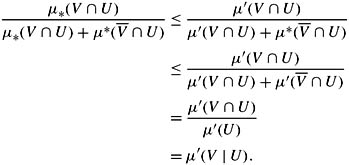
It remains to show that this bound is tight, that is, that there exists an extension μ₁ such that . This is also left as an exercise (Exercise 3.13).

It is immediate from Theorem 3.5.1 that μ_*(U | U) = μ*(U | U) = 1, as expected. Perhaps more interesting is the observation that if U is measurable, then μ_*(V | U) = μ_*(V ∩ U)/μ(U) and μ*(V | U) = μ*(V ∩ U)/μ(U). This follows easily from the fact that

(Exercise 3.14). The following example shows that the formulas for inner and outer measure also give intuitively reasonable answers in concrete examples:

Example 3.5.2

What happens if the three-prisoners puzzle is represented using non-measurable sets to capture the unknown probability that the jailer will say b given that a is pardoned? Let ′ consist of all the sets that can be formed by taking unions of lives -a, lives -b, and lives -c (where ∅ is considered to be the empty union); that is, lives -a, lives -b, and lives -c form a basis for ′. Since neither of the singleton sets {(a, b)} and {(a, c)} is in ′, no probability must be assigned to the event that the jailer will say b (resp., c) if a is pardoned. Note that all the measures in _J agree on the sets in ′. Let μ_J be the measure on ′ that agrees with each of the measures in _J. An easy computation shows that

(μ_J)_*(lives-a ∩ says-b) = (μ^J)_*({(a, b)}) = 0 (since the only element of ′ contained in {(a, b)} is the empty set);
(μ_J)*(lives-a ∩ says-b) = (μ_J)*({(a, b)}) = 1/3; and
(μ_J)*(lives-a ∩ says-b) = (μ_J)*(lives-a ∩ says-b) = μ({(c, b)}) = 1/3.

It follows from the arguments in Example 3.3.1 that

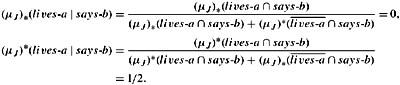
Just as Theorem 3.5.1 says, these equations give the lower and upper conditional probabilities of the set _J conditioned on the jailer saying b.