Getting Started
The following examples demonstrate how you can use the ROBUSTREG procedure to fit a linear regression model and conduct outlier and leverage point diagnostics.
M Estimation
This example shows how you can use the ROBUSTREG procedure to do M estimation, which is a commonly used method for outlier detection and robust regression when contamination is mainly in the response direction.
data stack; input x1 x2 x3 y; datalines; 80 27 89 42 80 27 88 37 75 25 90 37 62 24 87 28 62 22 87 18 62 23 87 18 62 24 93 19 62 24 93 20 58 23 87 15 58 18 80 14 58 18 89 14 58 17 88 13 58 18 82 11 58 19 93 12 50 18 89 8 50 18 86 7 50 19 72 8 50 19 79 8 50 20 80 9 56 20 82 15 70 20 91 15 ;
The data set stack is the well-known stackloss data set presented by Brownlee (1965). The data describe the operation of a plant for the oxidation of ammonia to nitric acid and consist of 21 four-dimensional observations. The explanatory variables for the response stackloss ( y ) are the rate of operation ( x1 ), the cooling water inlet temperature ( x2 ), and the acid concentration ( x3 ).
The following ROBUSTREG statements analyze the data:
proc robustreg data=stack; model y = x1 x2 x3 / diagnostics leverage; id x1; test x3; run;
By default, the procedure does M estimation with the bisquare weight function, and it uses the median method for estimating the scale parameter. The MODEL statement specifies the covariate effects. The DIAGNOSTICS option requests a table for outlier diagnostics, and the LEVERAGE option adds leverage point diagnostic results to this table for continuous covariate effects. The ID statement specifies that variable x1 is used to identify each observation in this table. If the ID statement is omitted, the observation number is used to identify the observations. The TEST statement requests a test of significance for the covariate effects specified. The results of this analysis are displayed in the following figures.
Figure 62.1 displays the model fitting information and summary statistics for the response variable and the continuous covariates. The columns labeled Q1, Median, and Q3 provide the lower quantile, median, and upper quantile. The column labeled MAD provides a robust estimate of the univariate scale, which is computed as the corrected median absolute deviation (MAD). The columns labeled Mean and Standard Deviation provide the usual mean and standard deviation. Large difference between the standard deviation and the MAD for a variable indicates some big jumps for this variable. In the stackloss data, the stackloss (reponse variable y ) has the biggest difference between the standard deviation and the dispersion.
| |
The ROBUSTREG Procedure Model Information Data Set WORK.STACK Dependent Variable y Number of Covariates 3 Number of Observations 21 Method M Estimation Summary Statistics Standard Variable Q1 Median Q3 Mean Deviation MAD x1 53.0000 58.0000 62.0000 60.4286 9.1683 5.9304 x2 18.0000 20.0000 24.0000 21.0952 3.1608 2.9652 x3 82.0000 87.0000 89.5000 86.2857 5.3586 4.4478 y 10.0000 15.0000 19.5000 17.5238 10.1716 5.9304
| |
Figure 62.1: Model Fitting Information and Summary Statistics
Figure 62.2 displays the table of robust parameter estimates, standard errors, and confidence limits. The row labeled Scale provides a point estimate of the scale parameter in the linear regression model, which is obtained by the median method. See the section 'M Estimation' on page 3993 for more information about scale estimation methods . For the stackloss data, M estimation yields the fitted linear model:
| |
The ROBUSTREG Procedure Parameter Estimates Standard 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 -42.2854 9.5045 60.9138 23.6569 19.79 <.0001 x1 1 0.9276 0.1077 0.7164 1.1387 74.11 <.0001 x2 1 0.6507 0.2940 0.0744 1.2270 4.90 0.0269 x3 1 0.1123 0.1249 0.3571 0.1324 0.81 0.3683 Scale 1 2.2819
| |
Figure 62.2: Model Parameter Estimates
Figure 62.3 displays outlier and leverage point diagnostics. Standardized robust residuals are computed based on the estimated parameters. Both the Mahalanobis distance and the robust MCD distance are displayed. Outliers and leverage points, identified with asterisks , are defined by the standardized robust residuals and robust MCD distances which exceed the corresponding cutoff values displayed in the diagnostics profile. Observations 4 and 21 are outliers because their standardized robust residuals exceed the cutoff value in absolute value. The procedure detects 4 observations with high leverage, which is contributed mainly by x1 , especially for the first three observations. This can be verified by the definition of the robust MCD distance in the section 'Robust Multivariate Location and Scale Estimates' on page 4009. Leverage points (points with high leverage) with smaller standardized robust residuals than the cutoff value in absolute value are called good leverage points; otherwise , called bad leverage points. Observations 21 is a bad leverage point.
| |
The ROBUSTREG Procedure Diagnostics Robust Standardized Mahalanobis MCD Robust Obs x1 Distance Distance Leverage Residual Outlier 1 80.000000 2.2536 5.5284 * 1.0995 2 80.000000 2.3247 5.6374 * -1.1409 3 75.000000 1.5937 4.1972 * 1.5604 4 62.000000 1.2719 1.5887 3.0381 * 21 70.000000 2.1768 3.6573 * -4.5733 * Diagnostics Summary Observation Type Proportion Cutoff Outlier 0.0952 3.0000 Leverage 0.1905 3.0575
| |
Figure 62.3: Diagnostics
Two particularly useful plots for revealing outliers and leverage points are a scatter plot of the standardized robust residuals against the robust distances (RDPLOT) and a scatter plot of the robust distances against the classical Mahalanobis distances (DDPLOT).
For the stackloss data, the following statements produce the RDPLOT in Figure 62.4 and the DDPLOT in Figure 62.5. The histogram and the normal quantilequantile plots for the standardized robust residuals are also created with the RESHISTOGRAM and RESQQPLOT options in the PROC statement. See Figure 62.6 and Figure 62.7.
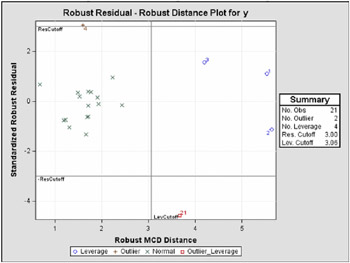
Figure 62.4: RDPLOT for Stackloss Data (Experimental)

Figure 62.5: DDPLOT for Stackloss Data (Experimental)
Figure 62.6: Histogram (Experimental)
Figure 62.7: Q-Q PLOT (Experimental)
ods html; ods graphics on; proc robustreg data=stack plots=(rdplot ddplot reshistogram resqqplot); model y = x1 x2 x3; run; ods graphics off; ods html close;
These plots are helpful in identifying outliers, good, and bad high leverage points.
These graphical displays are requested by specifying the experimental ODS GRAPHICS statement and the experimental PLOT PLOTS= optioninthePROC statement. For general information about ODS graphics, see Chapter 15, 'Statistical Graphics Using ODS.' For specific information about the graphics available in the ROBUSTREG procedure, see the section 'ODS Graphics' on page 4013.
Figure 62.8 displays robust versions of goodness-of-fit statistics for the model. You can use the robust information criteria, AICR and BICR, for model selection and comparison. For both AICR and BICR, the lower the value the more describable the model.
| |
The ROBUSTREG Procedure Goodness-of-Fit Statistic Value R-Square 0.6659 AICR 29.5231 BICR 36.3361 Deviance 125.7905
| |
Figure 62.8: Goodness-of-Fit
Figure 62.9 displays the test results requested by the TEST statement. The ROBUSTREG procedure conducts two robust linear tests, the -test and the ![]() -test. See the section 'Linear Tests' on page 3998 for information on how the procedure computes test statistics and the correction factor lambda . You can conclude that the effect x3 is not significant.
-test. See the section 'Linear Tests' on page 3998 for information on how the procedure computes test statistics and the correction factor lambda . You can conclude that the effect x3 is not significant.
| |
The ROBUSTREG Procedure Robust Linear Tests Test Test Chi- Test Statistic Lambda DF Square Pr > ChiSq Rho 0.9378 0.7977 1 1.18 0.2782 Rn2 0.8092 1 0.81 0.3683
| |
Figure 62.9: Test of Significance
For the bisquare weight function, the default constant c is 4.685 such that the asymptotic efficiency of the M estimates is 95% with the Gaussian distribution. See the section 'M Estimation' on page 3993 for details. The smaller the constant c ,the lower the asymptotic efficiency but the sharper the M estimate as an outlier detector. For the stackloss data set, you could consider using a sharper outlier detector.
In the following invocation of the ROBUSTREG procedure, a smaller constant, e.g. c =3 . 5, isused.
proc robustreg method=m(wf=bisquare(c=3.5)) data=stack; model y = x1 x2 x3 / diagnostics leverage; id x1; test x3; run;
Figure 62.10 displays the table of robust parameter estimates, standard errors, and confidence limits with the constant c =3 . 5. The refitted linear model is:
| |
The ROBUSTREG Procedure Parameter Estimates Standard 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 37.1076 5.4731 47.8346 26.3805 45.97 <.0001 x1 1 0.8191 0.0620 0.6975 0.9407 174.28 <.0001 x2 1 0.5173 0.1693 0.1855 0.8492 9.33 0.0022 x3 1 0.0728 0.0719 0.2138 0.0681 1.03 0.3111 Scale 1 1.4265
| |
Figure 62.10: Model Parameter Estimates
Figure 62.11 displays outlier and leverage point diagnostics with the constant c =3 . 5. Besides observations 4 and 21, observations 1 and 3 are also detected as outliers.
| |
The ROBUSTREG Procedure Diagnostics Robust Standardized Mahalanobis MCD Robust Obs x1 Distance Distance Leverage Residual Outlier 1 80.000000 2.2536 5.5284 * 4.2719 * 2 80.000000 2.3247 5.6374 * 0.7158 3 75.000000 1.5937 4.1972 * 4.4142 * 4 62.000000 1.2719 1.5887 5.7792 * 21 70.000000 2.1768 3.6573 * 6.2727 * Diagnostics Summary Observation Type Proportion Cutoff Outlier 0.1905 3.0000 Leverage 0.1905 3.0575 | |
Figure 62.11: Diagnostics
LTS Estimation
If the data are contaminated in the x -space, M estimation does not do well. The following example shows how you can use LTS estimation to deal with this situation.
data hbk; input index$ x1 x2 x3 y @@; datalines; 1 10.1 19.6 28.3 9.7 39 2.1 0.0 1.2 0.7 2 9.5 20.5 28.9 10.1 40 0.5 2.0 1.2 0.5 3 10.7 20.2 31.0 10.3 41 3.4 1.6 2.9 0.1 4 9.9 21.5 31.7 9.5 42 0.3 1.0 2.7 0.7 5 10.3 21.1 31.1 10.0 43 0.1 3.3 0.9 0.6 6 10.8 20.4 29.2 10.0 44 1.8 0.5 3.2 0.7 7 10.5 20.9 29.1 10.8 45 1.9 0.1 0.6 0.5 8 9.9 19.6 28.8 10.3 46 1.8 0.5 3.0 0.4 9 9.7 20.7 31.0 9.6 47 3.0 0.1 0.8 0.9 10 9.3 19.7 30.3 9.9 48 3.1 1.6 3.0 0.1 11 11.0 24.0 35.0 0.2 49 3.1 2.5 1.9 0.9 12 12.0 23.0 37.0 0.4 50 2.1 2.8 2.9 0.4 13 12.0 26.0 34.0 0.7 51 2.3 1.5 0.4 0.7 14 11.0 34.0 34.0 0.1 52 3.3 0.6 1.2 0.5 15 3.4 2.9 2.1 0.4 53 0.3 0.4 3.3 0.7 16 3.1 2.2 0.3 0.6 54 1.1 3.0 0.3 0.7 17 0.0 1.6 0.2 0.2 55 0.5 2.4 0.9 0.0 18 2.3 1.6 2.0 0.0 56 1.8 3.2 0.9 0.1 19 0.8 2.9 1.6 0.1 57 1.8 0.7 0.7 0.7 20 3.1 3.4 2.2 0.4 58 2.4 3.4 1.5 0.1 21 2.6 2.2 1.9 0.9 59 1.6 2.1 3.0 0.3 22 0.4 3.2 1.9 0.3 60 0.3 1.5 3.3 0.9 23 2.0 2.3 0.8 0.8 61 0.4 3.4 3.0 0.3 24 1.3 2.3 0.5 0.7 62 0.9 0.1 0.3 0.6 25 1.0 0.0 0.4 0.3 63 1.1 2.7 0.2 0.3 26 0.9 3.3 2.5 0.8 64 2.8 3.0 2.9 0.5 27 3.3 2.5 2.9 0.7 65 2.0 0.7 2.7 0.6 28 1.8 0.8 2.0 0.3 66 0.2 1.8 0.8 0.9 29 1.2 0.9 0.8 0.3 67 1.6 2.0 1.2 0.7 30 1.2 0.7 3.4 0.3 68 0.1 0.0 1.1 0.6 31 3.1 1.4 1.0 0.0 69 2.0 0.6 0.3 0.2 32 0.5 2.4 0.3 0.4 70 1.0 2.2 2.9 0.7 33 1.5 3.1 1.5 0.6 71 2.2 2.5 2.3 0.2 34 0.4 0.0 0.7 0.7 72 0.6 2.0 1.5 0.2 35 3.1 2.4 3.0 0.3 73 0.3 1.7 2.2 0.4 36 1.1 2.2 2.7 1.0 74 0.0 2.2 1.6 0.9 37 0.1 3.0 2.6 0.6 75 0.3 0.4 2.6 0.2 38 1.5 1.2 0.2 0.9 ;
The data set hbk is an artificial data set generated by Hawkins, Bradu, and Kass (1984). Both ordinary least squares (OLS) estimation and M estimation (not shown here) suggest that observations 11 to 14 are serious outliers. However, these four observations were generated from the underlying model, whereas observations 1 to 10 were contaminated. The reason that OLS estimation and M estimation do not pick up the contaminated observations is that they cannot distinguish good leverage points (observations 11 to 14) from bad leverage points (observations 1 to 10). In such cases, the LTS method identifies the true outliers.
The following statements invoke the ROBUSTREG procedure with the LTS estimation method.
proc robustreg data=hbk fwls method=lts; model y = x1 x2 x3 / diagnostics leverage; id index; run;
Figure 62.12 displays the model fitting information and summary statistics for the response variable and independent covariates.
| |
The ROBUSTREG Procedure Model Information Data Set WORK.HBK Dependent Variable y Number of Covariates 3 Number of Observations 75 Method LTS Estimation Summary Statistics Standard Variable Q1 Median Q3 Mean Deviation MAD x1 0.8000 1.8000 3.1000 3.2067 3.6526 1.9274 x2 1.0000 2.2000 3.3000 5.5973 8.2391 1.6309 x3 0.9000 2.1000 3.0000 7.2307 11.7403 1.7791 y 0.5000 0.1000 0.7000 1.2787 3.4928 0.8896 | |
Figure 62.12: Model Fitting Information and Summary Statistics
Figure 62.13 displays information about the LTS fit, which includes the breakdown value of the LTS estimate. Roughly speaking, the breakdown value is a measure of the proportion of contamination that an estimation method can withstand and still maintain its robustness. In this example the LTS estimate minimizes the sum of 57 smallest squares of residuals. It can still pick up the right model if the remaining 18 observations are contaminated. This corresponds to the breakdown value around 0.25, which is set as the default.
| |
The ROBUSTREG Procedure LTS Profile Total Number of Observations 75 Number of Squares Minimized 57 Number of Coefficients 4 Highest Possible Breakdown Value 0.2533
| |
Figure 62.13: LTS Profile
Figure 62.14 displays parameter estimates for covariates and scale. Two robust estimates of the scale parameter are displayed. See the section 'Final Weighted Scale Estimator' on page 4002 for how these estimates are computed. The weighted scale estimate (Wscale) is a more efficient estimate of the scale parameter.
| |
The ROBUSTREG Procedure LTS Parameter Estimates Parameter DF Estimate Intercept 1 0.3431 x1 1 0.0901 x2 1 0.0703 x3 1 0.0731 Scale (sLTS) 0 0.7451 Scale (Wscale) 0 0.5749
| |
Figure 62.14: LTS Parameter Estimates
Figure 62.15 displays outlier and leverage point diagnostics. The ID variable index is used to identify the observations. The first ten observations are identified as outliers and observations 11 to 14 are identified as good leverage points.
| |
The ROBUSTREG Procedure Diagnostics Robust Standardized Mahalanobis MCD Robust Obs index Distance Distance Leverage Residual Outlier 1 1 1.9168 29.4424 * 17.0868 * 3 2 1.8558 30.2054 * 17.8428 * 5 3 2.3137 31.8909 * 18.3063 * 7 4 2.2297 32.8621 * 16.9702 * 9 5 2.1001 32.2778 * 17.7498 * 11 6 2.1462 30.5892 * 17.5155 * 13 7 2.0105 30.6807 * 18.8801 * 15 8 1.9193 29.7994 * 18.2253 * 17 9 2.2212 31.9537 * 17.1843 * 19 10 2.3335 30.9429 * 17.8021 * 21 11 2.4465 36.6384 * 0.0406 23 12 3.1083 37.9552 * 0.0874 25 13 2.6624 36.9175 * 1.0776 27 14 6.3816 41.0914 * 0.7875 Diagnostics Summary Observation Type Proportion Cutoff Outlier 0.1333 3.0000 Leverage 0.1867 3.0575
| |
Figure 62.15: Diagnostics
Figure 62.16 specifies the number These estimates are least squares estimates computed after deleting the detected outliers.
| |
The ROBUSTREG Procedure Parameter Estimates for Final Weighted Least Squares Fit Standard 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 0.1805 0.1044 0.3852 0.0242 2.99 0.0840 x1 1 0.0814 0.0667 0.0493 0.2120 1.49 0.2222 x2 1 0.0399 0.0405 0.0394 0.1192 0.97 0.3242 x3 1 0.0517 0.0354 0.1210 0.0177 2.13 0.1441 Scale 0 0.5572
| |
Figure 62.16: Final Weighted LS Estimates