Chapter 19: The CALIS Procedure | SAS/STAT 9.1 Users Guide, Volumes 1-7

Overview

Structural equation modeling using covariance analysis is an important statistical tool in economics and behavioral sciences. Structural equations express relationships among several variables that can be either directly observed variables (manifest variables) or unobserved hypothetical variables (latent variables). For an introduction to latent variable models, refer to Loehlin (1987), Bollen (1989b), Everitt (1984), or Long (1983); and for manifest variables, refer to Fuller (1987).

In structural models, as opposed to functional models, all variables are taken to be random rather than having fixed levels. For maximum likelihood (default) and generalized least-squares estimation in PROC CALIS, the random variables are assumed to have an approximately multivariate normal distribution. Nonnormality, especially high kurtosis , can produce poor estimates and grossly incorrect standard errors and hypothesis tests, even in large samples. Consequently, the assumption of normality is much more important than in models with nonstochastic exogenous variables. You should remove outliers and consider transformations of nonnormal variables before using PROC CALIS with maximum likelihood (default) or generalized least-squares estimation. If the number of observations is sufficiently large, Browne's asymptotically distribution-free (ADF) estimation method can be used.

You can use the CALIS procedure to estimate parameters and test hypotheses for constrained and unconstrained problems in

multiple and multivariate linear regression
linear measurement-error models
path analysis and causal modeling
simultaneous equation models with reciprocal causation
exploratory and confirmatory factor analysis of any order
canonical correlation
a wide variety of other (non)linear latent variable models

The parameters are estimated using the criteria of

unweighted least squares (ULS)
generalized least squares (GLS, with optional weight matrix input)
maximum likelihood (ML, for multivariate normal data)
weighted least squares (WLS, ADF, with optional weight matrix input)
diagonally weighted least squares (DWLS, with optional weight matrix input)

The default weight matrix for generalized least-squares estimation is the sample covariance or correlation matrix. The default weight matrix for weighted least-squares estimation is an estimate of the asymptotic covariance matrix of the sample covariance or correlation matrix. In this case, weighted least-squares estimation is equivalent to Browne's (1982, 1984) asymptotic distribution-free estimation. The default weight matrix for diagonally weighted least-squares estimation is an estimate of the asymptotic variances of the input sample covariance or correlation matrix. You can also use an input data set to specify the weight matrix in GLS, WLS, and DWLS estimation.

You can specify the model in several ways:

You can do a constrained (confirmatory) first-order factor analysis or component analysis using the FACTOR statement.
You can specify simple path models using an easily formulated list-type RAM statement similar to that originally developed by J. McArdle (McArdle and McDonald 1984).
If you have a set of structural equations to describe the model, you can use an equation-type LINEQS statement similar to that originally developed by P. Bentler (1985).
You can analyze a broad family of matrix models using COSAN and MATRIX statements that are similar to the COSAN program of R. McDonald and C. Fraser (McDonald 1978, 1980). It enables you to specify complex matrix models including nonlinear equation models and higher-order factor models.

You can specify linear and nonlinear equality and inequality constraints on the parameters with several different statements, depending on the type of input. Lagrange multiplier test indices are computed for simple constant and equality parameter constraints and for active boundary constraints. General equality and inequality constraints can be formulated using program statements. For more information, see the 'SAS Program Statements' section on page 628.

PROC CALIS offers a variety of methods for the automatic generation of initial values for the optimization process:

two-stage least-squares estimation
instrumental variable factor analysis
approximate factor analysis
ordinary least-squares estimation
McDonald's (McDonald and Hartmann 1992) method

In many common applications, these initial values prevent computational problems and save computer time.

Because numerical problems can occur in the (non)linearly constrained optimization process, the CALIS procedure offers several optimization algorithms:

Levenberg-Marquardt algorithm (Mor , 1978)
trust region algorithm (Gay 1983)
Newton-Raphson algorithm with line search
ridge-stabilized Newton-Raphson algorithm
various quasi-Newton and dual quasi-Newton algorithms: Broyden-Fletcher-Goldfarb-Shanno and Davidon-Fletcher-Powell, including a sequential quadratic programming algorithm for processing nonlinear equality and inequality constraints
various conjugate gradient algorithms: automatic restart algorithm of Powell (1977), Fletcher-Reeves, Polak-Ribiere, and conjugate descent algorithm of Fletcher (1980)

The quasi-Newton and conjugate gradient algorithms can be modified by several linesearch methods. All of the optimization techniques can impose simple boundary and general linear constraints on the parameters. Only the dual quasi-Newton algorithm is able to impose general nonlinear equality and inequality constraints.

The procedure creates an OUTRAM= output data set that completely describes the model (except for program statements) and also contains parameter estimates. This data set can be used as input for another execution of PROC CALIS. Small model changes can be made by editing this data set, so you can exploit the old parameter estimates as starting values in a subsequent analysis. An OUTEST= data set contains information on the optimal parameter estimates (parameter estimates, gradient, Hessian, projected Hessian and Hessian of Lagrange function for constrained optimization, the information matrix, and standard errors). The OUTEST= data set can be used as an INEST= data set to provide starting values and boundary and linear constraints for the parameters. An OUTSTAT= data set contains residuals and, for exploratory factor analysis, the rotated and unrotated factor loadings.

Automatic variable selection (using only those variables from the input data set that are used in the model specification) is performed in connection with the RAM and LINEQS input statements or when these models are recognized in an input model file. Also in these cases, the covariances of the exogenous manifest variables are recognized as given constants. With the PREDET option, you can display the predetermined pattern of constant and variable elements in the predicted model matrix before the minimization process starts. For more information, see the section 'Automatic Variable Selection' on page 662 and the section 'Exogenous Manifest Variables' on page 662.

PROC CALIS offers an analysis of linear dependencies in the information matrix (approximate Hessian matrix) that may be helpful in detecting unidentified models. You also can save the information matrix and the approximate covariance matrix of the parameter estimates (inverse of the information matrix), together with parameter estimates, gradient, and approximate standard errors, in an output data set for further analysis.

PROC CALIS does not provide the analysis of multiple samples with different sample size or a generalized algorithm for missing values in the data. However, the analysis of multiple samples with equal sample size can be performed by the analysis of a moment supermatrix containing the individual moment matrices as block diagonal submatrices.

Structural Equation Models

The Generalized COSAN Model

PROC CALIS can analyze matrix models of the form

where C is a symmetric correlation or covariance matrix, each matrix F _k , k = 1 , ..., m, is the product of n ( k ) matrices , and each matrix P _k is symmetric, that is,

The matrices and P _k in the model are parameterized by the matrices and Q _k

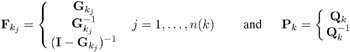
where you can specify the type of matrix desired.

The matrices and Q _k can contain

constant values
parameters to be estimated
values computed from parameters via programming statements

The parameters can be summarized in a parameter vector X = ( x ₁ , ..., x _t ). For a given covariance or correlation matrix C , PROC CALIS computes the unweighted least-squares (ULS), generalized least-squares (GLS), maximum likelihood (ML), weighted least-squares (WLS), or diagonally weighted least-squares (DWLS) estimates of the vector X .

Some Special Cases of the Generalized COSAN Model

Original COSAN (Covariance Structure Analysis) Model (McDonald 1978, 1980)

Covariance Structure:

RAM (Reticular Action) Model (McArdle 1980; McArdle and McDonald 1984)

Structural Equation Model:

where A is a matrix of coefficients, and v and u are vectors of random variables. The variables in v and u can be manifest or latent variables. The endogenous variables corresponding to the components in v are expressed as a linear combination of the remaining variables and a residual component in u with covariance matrix P .

Covariance Structure:

with selection matrix J and

LINEQS (Linear Equations) Model (Bentler and Weeks 1980)

Structural Equation Model:

where ² and ³ are coefficient matrices, and · and ¾ are vectors of random variables. The components of · correspond to the endogenous variables; the components of ¾ correspond to the exogenous variables and to error variables. The variables in · and ¾ can be manifest or latent variables. The endogenous variables in · are expressed as a linear combination of the remaining endogenous variables, of the exogenous variables of ¾ , and of a residual component in ¾ . The coefficient matrix ² describes the relationships among the endogenous variables of · , and I ˆ’ ² should be nonsingular. The coefficient matrix ³ describes the relationships between the endogenous variables of · and the exogenous and error variables of ¾ .

Covariance Structure:

with selection matrix J , = µ { ¾¾ ' }, and

Keesling - Wiley - J reskog LISREL (Linear Structural Relationship) Model

Structural Equation Model and Measurement Models:

where · and ¾ are vectors of latent variables (factors), and x and y are vectors of manifest variables. The components of · correspond to endogenous latent variables; the components of ¾ correspond to exogenous latent variables. The endogenous and exogenous latent variables are connected by a system of linear equations (the structural model) with coefficient matrices B and “ and an error vector . It is assumed that matrix I ˆ’ B is nonsingular. The random vectors y and x correspond to manifest variables that are related to the latent variables · and ¾ by two systems of linear equations (the measurement model) with coefficients _y and _x and with measurement errors µ and .

Covariance Structure:

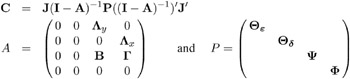
with selection matrix J , = µ { ¾¾ ² }, = µ { ² }, ˜ = µ { ' }, and ˜ _µ = µ { µµ ² }.

Higher-Order Factor Analysis Models

First-order model:

Second-order model:

First-Order Autoregressive Longitudinal Factor Model

Example of McDonald (1980): k=3: Occasions of Measurement; n=3: Variables (Tests); m=2: Common Factors

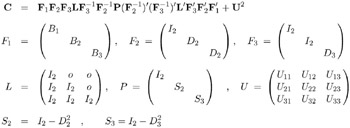
For more information on this model, see Example 19.6 on page 739.

A Structural Equation Example

This example from Wheaton et al. (1977) illustrates the relationships among the RAM, LINEQS, and LISREL models. Different structural models for these data are in J reskog and S rbom (1985) and in Bentler (1985, p. 28). The data set contains covariances among six (manifest) variables collected from 932 people in rural regions of Illinois:

Variable 1:	V 1 , y ₁ : Anomia 1967
Variable 2:	V 2 , y ₂ : Powerlessness 1967
Variable 3:	V 3 , y ₃ : Anomia 1971
Variable 4:	V 4 , y ₄ : Powerlessness 1971
Variable 5:	V 5 , x ₁ : Education ( years of schooling)
Variable 6:	V 6 , x ₂ : Duncan's Socioeconomic Index (SEI)

It is assumed that anomia and powerlessness are indicators of an alienation factor and that education and SEI are indicators for a socioeconomic status (SES) factor. Hence, the analysis contains three latent variables:

Variable 7:	F 1, · ₁ : Alienation 1967
Variable 8:	F 2, · ₂ : Alienation 1971
Variable 9:	F 3, ¾ ₁ : Socioeconomic Status (SES)

The following path diagram shows the structural model used in Bentler (1985, p. 29) and slightly modified in J reskog and S rbom (1985, p. 56). In this notation for the path diagram, regression coefficients between the variables are indicated as one-headed arrows. Variances and covariances among the variables are indicated as two-headed arrows. Indicating error variances and covariances as two-headed arrows with the same source and destination (McArdle 1988; McDonald 1985) is helpful in transforming the path diagram to RAM model list input for the CALIS procedure.

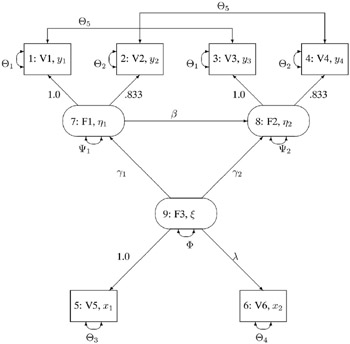
Figure 19.1: Path Diagram of Stability and Alienation Example

Variables in Figure 19.1 are as follows :

Variable 1:	V 1 , y ₁ : Anomia 1967
Variable 2:	V 2 , y ₂ : Powerlessness 1967
Variable 3:	V 3 , y ₃ : Anomia 1971
Variable 4:	V 4 , y ₄ : Powerlessness 1971
Variable 5:	V 5 , x ₁ : Education (years of schooling)
Variable 6:	V 6 , x ₂ : Duncan's Socioeconomic Index (SEI)
Variable 7:	F 1, · ₁ : Alienation 1967
Variable 8:	F 2, · ₂ : Alienation 1971
Variable 9:	F 3, ¾ ₁ : Socioeconomic Status (SES)

RAM Model

The vector v contains the six manifest variables v ₁ = V 1 ,...,v ₆ = V 6 and the three latent variables v ₇ = F 1 ,v ₈ = F 2 , v ₉ = F 3. The vector u contains the corresponding error variables u ₁ = E 1 ,...,u ₆ = E 6 and u ₇ = D 1 , u ₈ = D 2 , u ₉ = D 3. The path diagram corresponds to the following set of structural equations of the RAM model:

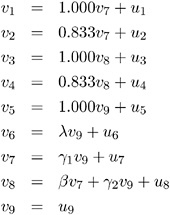
This gives the matrices A and P in the RAM model:

The RAM model input specification of this example for the CALIS procedure is in the 'RAM Model Specification' section on page 563.

LINEQS Model

The vector · contains the six endogenous manifest variables V 1, ... , V 6 and the two endogenous latent variables F 1 and F 2. The vector ¾ contains the exogenous error variables E 1, ... , E 6, D 1, and D 2 and the exogenous latent variable F 3. The path diagram corresponds to the following set of structural equations of the LINEQS model:

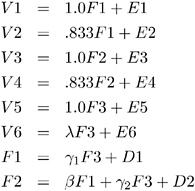
This gives the matrices ² , ³ and in the LINEQS model:

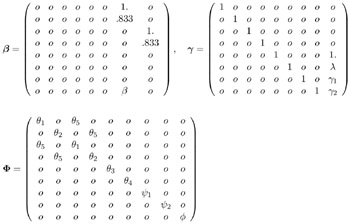
The LINEQS model input specification of this example for the CALIS procedure is in the section 'LINEQS Model Specification' on page 562.

LISREL Model

The vector y contains the four endogenous manifest variables y ₁ = V 1 , ..., y ₄ = V 4 , and the vector x contains the exogenous manifest variables x ₁ = V 5 and x ₂ = V 6. The vector µ contains the error variables µ ₁ = E 1 , ..., µ ₄ = E 4 corresponding to y , and the vector contains the error variables ₁ = E 5 and ₂ = E 6 corresponding to x . The vector · contains the endogenous latent variables (factors) · ₁ = F 1 and · ₂ = F 2, while the vector ¾ contains the exogenous latent variable (factor) ¾ ₁ = F 3. The vector contains the errors ₁ = D 1 and ₂ = D 2 in the equations (disturbance terms) corresponding to · . The path diagram corresponds to the following set of structural equations of the LISREL model:

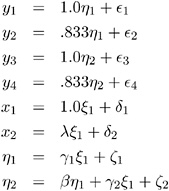
This gives the matrices _y , _x , B , “ , and in the LISREL model:

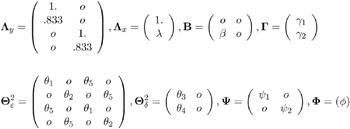
The CALIS procedure does not provide a LISREL model input specification. However, any model that can be specified by the LISREL model can also be specified by using the COSAN, LINEQS, or RAM model specifications in PROC CALIS.