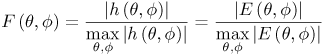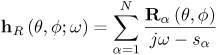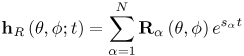Section 4.2. Antenna Measurements and Modeling in the Time Domain
|
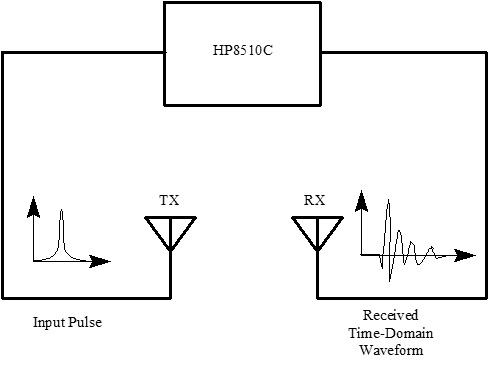
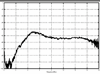
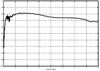
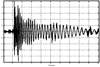
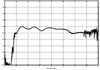
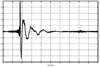
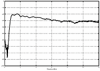
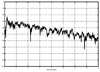
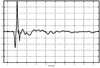
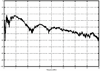
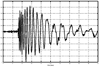
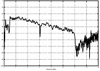
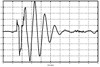
4.2. Antenna Measurements and Modeling in the Time Domain4.2.1. Basic ResponsesClassic antenna measurements include pattern and impedance versus frequency. The pattern is often measured for both co-polarized and cross-polarized components of the antenna as defined in terms of the expected antenna performance. As an alternative to impedance, voltage-standing-wave ratio (VSWR) or return loss are often used as a measure of how closely an antenna is matched to a reference impedance. Each of these terms requires further consideration for transient analysis. However, we first review the basic concepts in the frequency domain to provide a common foundation. The pattern is expressed in terms of the electric or magnetic field received at a fixed distance in the far field as the angular position is changed about the antenna. It is also common to normalize the pattern to the maximum value. Historically, patterns were measured in amplitude only, though modern ranges provide useful phase information. The classic dipole antenna consists of a half wavelength of wire, fed at the center. The pattern, F, of such an antenna is a figure eight, denoted by Equation 4.57 In a more general form, and in the context of our previous development of effective length, the normalized pattern is given as Equation 4.58 for the electric field magnitude. The pattern can also be defined for each polarization or in terms of the power. Three-dimensional patterns are sometimes desired, but they are very time consuming to measure and difficult to display. To overcome these limitations, it is common to plot polar plots in planar or conical cuts of the antenna. Planar cuts are often selected to correspond to major axes of the antenna and are defined in terms of planes in which the electric or magnetic field intensities are parallel, called the E plane and H plane, respectively. In this sense, both co-polarized and cross-polarized fields can be plotted relative to the expected polarization. A conical cut provides a plot versus azimuth for a specified elevation angle. A typical plot for the dipole is displayed in Figure 4.3. Figure 4.3. The Pattern of a Dipole Antenna in the E Plane (elevation). The Pattern is Independent of f and the Azimuthal Cut is Omni-Directional.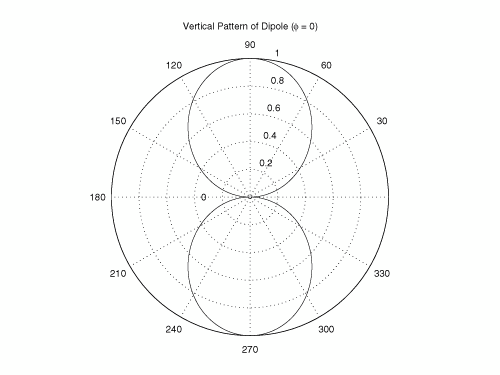 The input impedance of the antenna provides the necessary information for the design of a matching section for maximum power transfer or for the evaluation of the quality of the match to a transmission system. The impedance is often plotted on a Smith chart or in terms of either reflection coefficient magnitude or voltage-standing-wave ratio (VSWR) to denote the quality of the match to a reference impedance as in Figure 4.4. Figure 4.4. The Impedance of a Dipole Antenna for a Variety of Forms. 4.2.2. UWB PerformanceFor UWB applications, we need to evaluate the antenna in terms of the modulation format of interest. Both I-UWB systems and MC-UWB systems must be considered. For pulse systems, instantaneous wideband performance is required, with a linear phase response. The linear phase response is necessary to avoid dispersion that creates pulse distortion at a nanosecond delay. For MC-UWB systems, each channel is relatively narrowband compared to UWB, and dispersion relative to the pulse shape is no longer critical, requiring only gain and related parameters as in classic analysis. Synchronization is still important for MC-UWB systems and is simply obtained by incorporating pilot-carrier techniques for each channel. In the latter situation, only the frequency amplitude response of the basic channels is necessary for the system. For the pulse system, the pulse amplitude and shape of the transmission waveform and the reflection properties of the antenna are the basic representations for the antenna response. These terms include the information necessary for the MC-UWB system as well as the transient system. Insight is also provided into the operation of the antenna and channel that is often missed with the frequency-domain representation. The properties of the resonant monopole, cavity-backed Archimedean spiral (CBAS), and TEM horn antennas are investigated in terms of their impulse and frequency responses and their usefulness in UWB technology based on duration, type, and amplitude of the radiated transient waveform. Additional data on the log-periodic toothed trapezoid (LPTTA), Vivaldi, and biconical antennas are also summarized. The frequency response needed for MC-UWB systems is also provided. To perform the measurements for radiation performance, two identical antennas were measured in a LOS link using an HP8510 network analyzer. A 20 GHz spectrum was used, corresponding to a 50% pulse width of 50 ps. The impulse response, transmission coefficient, and reflection coefficient were all measured using the measurement setup illustrated in Figure 4.5. Figure 4.5. Measurement Setup for the Frequency and Impulse Response.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. Resonant MonopoleA Narrowband ExampleThe mechanisms of dipole radiation, excited by a short pulse, have been investigated by many authors, and some of the results have been reported in [813]. Only the note by Bantin [10] discusses the possibility of using a pair of 2 meter long dipoles as a link for UWB communications. For UWB antenna and link characterization, the time domain approach provides more insight than a classical frequency domain analysis [8]. The monopole antenna structure performance is similar to a dipole due to the image of the monopole in a ground plane depicted in Figure 4.6. Figure 4.6. Monopole on a Finite Ground Plane. The typical frequency response shown in Figure 4.7 for a 5 GHz monopole pair highlights the transmission performance. The frequency response shows the most efficient transmission at the resonant frequency around 5.0 GHz, with a signal amplitude decay of 1 dB/GHz as the frequency increases from 4 GHz to 13 GHz. The Friis transmission (4.51) suggests that this decay represents a constant gain antenna above the basic resonance, with the decay due to the inverse frequency relation between gain and effective aperture. However, care must be taken with such a claim to ensure that the input reflection is also low over these frequencies. If the reflection is not low we may actually find the antenna has a general gain increase as the frequency is increased, with a mismatch that counters this increase to give us an effective constant gain on the boresight. The overall dipole response on the boresight does appear to have an equivalent constant gain effect, but also has a substantial mismatch loss (see Figure 4.8) as the frequency increases. Figure 4.7. The Frequency and Transient Response Waveforms of the Monopole Link.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 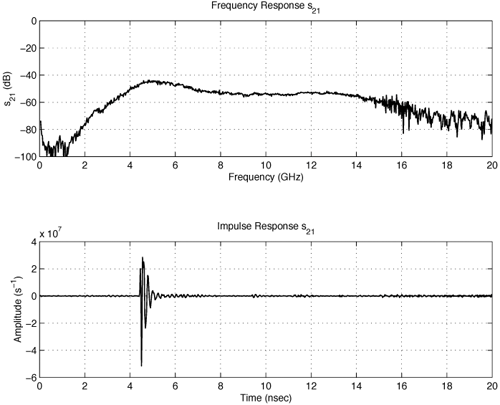 Figure 4.8. The Monopole Return Loss and Transmission Phase.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. Used by permission. 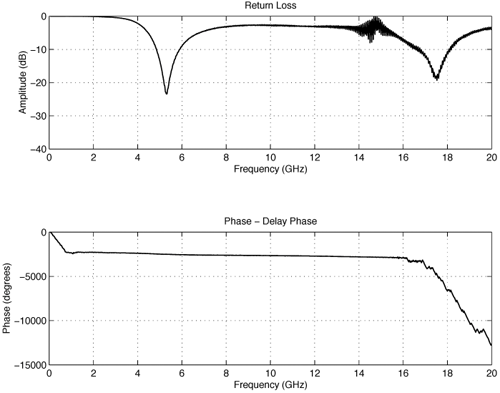 The corresponding impulse response is shown in Figure 4.7. The measured waveform is not a clear doublet, but has a damped ringing that would be expected about the monopole resonance. The damped ringing has a duration of 1.00 ns. The peak amplitude is lower than the amplitude of classic UWB antennas due to the mismatch. Late time effects of diffraction from the back edge of the finite ground plane for our monopole example occur at 9.5 ns, but are small. Each monopole was tuned to a resonant frequency of 5 GHz. Four loss mechanisms may exist in this link: pattern, space loss, gain to aperture loss, and reflection at the antenna terminals. All mechanisms contribute to the overall equivalent efficiency of the system. Even with these limitations, the experimental results indicate that two resonant monopoles may be used in a UWB communication link with pulse modulation. The main drawbacks relate to efficiency and a slight damped ringing. The efficiency can be improved by using a fat or sleeve dipole/monopole arrangement. Cavity-Backed Archimedean Spiral (CBAS)A Frequency Independent AntennaThe Archimedean spiral shown in Figure 4.9 is a classic frequency-independent antenna [1]. The phase of the antenna varies nonlinearly with frequency and can be explained by physically tracing the path of a transmitted pulse along the spiral. As the pulse travels from the center of the spiral towards the edge, radiation occurs. The higher-frequency signal components are radiated near the center, followed by the lower-frequency components towards the outside, causing frequency dispersion. This antenna has a wide operating frequency range of 2.0 to 18.0 GHz, but frequency dispersion makes it unacceptable for UWB pulse applications. For MC-UWB applications, it provides circular polarization and would meet the basic need as long as a pilot carrier is transmitted with each carrier to ensure synchronization. Indeed, the MC-UWB application is consistent with the frequency-independent nature of the antenna that is generally used for narrowband applications that can be tuned within the band of the antenna. Figure 4.9. Geometry of an Archimedean Spiral Antenna.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. The presence of the frequency dispersion of the cavity-backed Archimedean spiral is illustrated in Figure 4.10. The antenna demonstrates a ringing with a frequency shift. The frequency shift is due to the phase delays experienced by the different frequency components of the radiated field, giving rise to a chirp duration of 13.5 ns. Figure 4.11 shows the frequency match and transmission phase response. This type of antenna has the desired magnitude frequency response over the entire frequency band. However, the phase response has an undesired nonlinear behavior above the 2 GHz lower frequency that produces severe dispersion with a frequency chirp. Figure 4.10. The Frequency and Transient Response Waveforms of the Cavity-Backed Archimedean Spiral Link.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 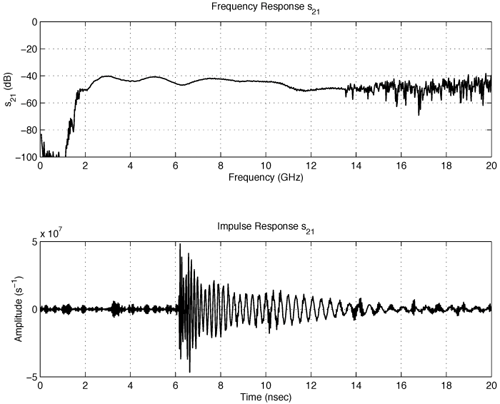 Figure 4.11. The Cavity-Backed Archimedean Spiral Return Loss and Transmission Phase.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 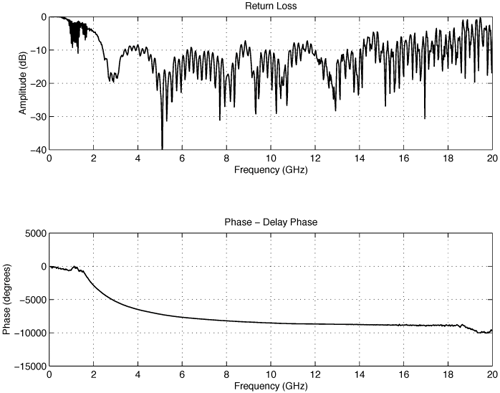 TEM HornA UWB AntennaThe TEM (transverse electric and magnetic) horn is a traveling-wave antenna. TEM horns have been traditionally used for low-dispersion launching and receiving of UWB pulses [14]. Research conducted since the late 1970s has led to a further reduction of dispersion caused by the TEM horn abrupt edges. Figure 4.12 shows the basic TEM horn geometry. Figure 4.12. Geometry of the TEM Horn Antenna.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. In order to suppress the reflection from the TEM horn edges, the antenna is commonly loaded with chip resistors or a conductive film. Some authors have shown experiments with tapered resistive coatings that absorb the wave at the tip of the horn [15]. Figure 4.13 shows a TEM horn mounted over a ground plane, having a operating frequency range of approximately 1 to 18 GHz. Figure 4.13. The TEM Horn Antenna.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. The TEM horn impulse response shown in Figure 4.14 is a highly damped sinusoid with a duration of Figure 4.14. The Frequency and Transient Response Waveforms of the TEM Horn Antenna Link.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation, [7]. © S. Licul, 2004. Used by permission. 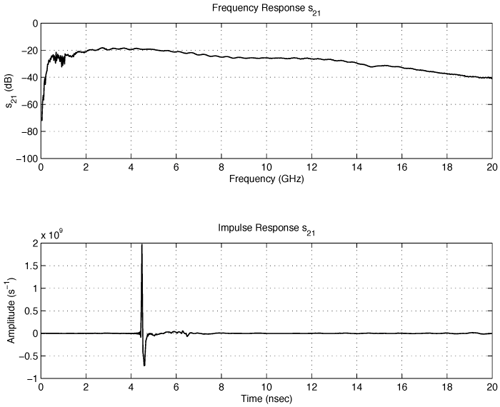 Figure 4.15. The TEM Horn Return Loss and Phase.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 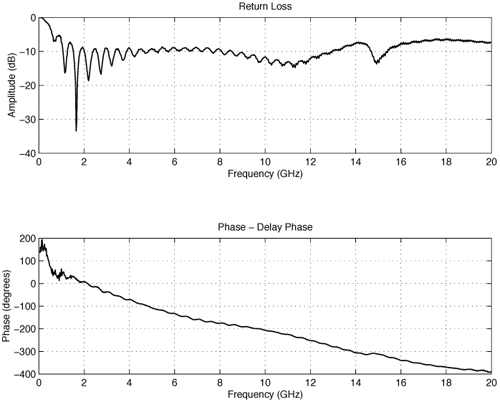 Finally, the TEM horn can be used as a source for radiation through a tapered aperture. A tapered aperture reduces reflections of the aperture edges, thus enabling the incident wave to have a smoother transition. This configuration also achieves lower side lobes. Summary of Potential UWB Antenna StructuresThe antennas presented represent classic narrowband, frequency-independent (wide-band), and UWB performance. The antennas presented are compared to several other antennas in Table 4.1.
The basic structure, transient impulse response, and frequency response are shown for each antenna. The Archimedean spiral is an American Electronic Laboratories model AST-1492AA with a range of 2.018.0 GHz; the ridged TEM horn is an Antenna Research Associates model DRG-118/A with a range of 1.018.0 GHz; and the log-periodic toothed structure is an American Electronic Laboratories model APN-101B with a range of 1.012.4 GHz. The remaining antennas were built in-house and represent typical dimensions for such structures. The comparison of these different classical broadband structures with regards to possible use in pulse UWB communications offers some interesting observations (see Table 4.2). The received peak amplitude in the far field obeys a 1/ distance decrease in amplitude relative to the measured peak. The pulse shape, in general, will always stay the same and is not a function of distance, but it is dependent on the antenna geometry and angular orientation.
It can be seen that for directional applications the Vivaldi offers a good option, with a single-cycle sinusoid at the output, similar to the TEM horn. For omnidirectional antennas, the monopole performs fairly well, though with a lower amplitude. Typical broadband structures, such as the log-periodic array and Archimedean spiral, suffer from an acute phase dispersion, rendering them undesirable for impulse UWB communication, but they can still be used for MC-UWB (multichannel) systems. 4.2.3. Frequency and Time RelationshipsObserving the behavior of the UWB antennas in Table 4.1 we see a common trend in the transfer response. Basically the response has a resonance that splits the spectrum into two parts. In the region below resonance, the antennas act as constant effective-length structures, and the response is one of a capacitive mismatch with an w3 link response due to the combination of the mismatch and the w of the link. Above the resonant frequency, fr, the antennas generally act as constant gain antennas with a link response of 1/w. These results are summarized in Figure 4.16. Figure 4.16. Simple Representation of the Link Response of a UWB Antenna. The behavior in the vicinity of resonance is also important in the damping response of the system. If the maximum is peaked, the damping tends to be reduced, leading to a ringing of the response. For a smooth response, we have the form of the system transmission, s21, of Figure 4.17, and a corresponding result for a peaked response in Figure 4.18. Figure 4.17. Response for a Slow Variation About Resonance.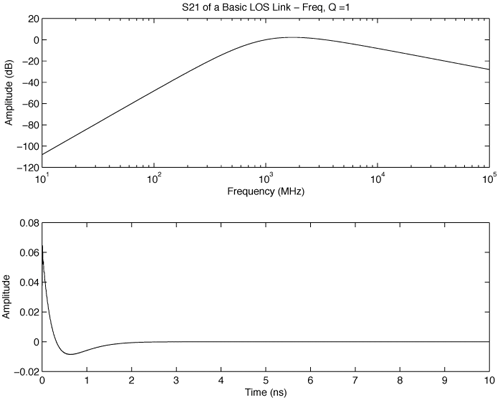 Figure 4.18. Response for a Peaked Resonance. The latter represents the response typically obtained with a dipole. However, the constant gain conclusion for the dipole would be in error. As the frequency applied to a dipole increases, the gain actually tends to increase and focus to a narrower beam. The reason for the apparent constant-gain response is the result of the mismatch of the antenna. For the constant-gain observation to be valid the antenna must be well matched to the system. 4.2.4. Pattern Concept in TimeThe concept of visualizing an antenna pattern in the time domain requires additional thought. In the frequency domain, we represent that pattern by plots similar to those of Figure 4.3. If the antenna behaves the same way over the bandwidth, the radiation pattern for a single frequency can be used. However, this frequency domain concept does not generalize easily to the time domain. There are two common methods for representing the pattern of an antenna in the time domain. Peak amplitude is the critical component for threshold detection in pulse systems. However, this peak information is limited, and it is common to represent the pattern by a collection of waveforms versus angle. Both of these representations are shown in Figure 4.19. Figure 4.19. Pattern Concepts for UWB.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 4.2.5. Time Domain Modeling (A Minimal Approach)A pole-residue model provides a minimal representation for the antenna that is particularly useful for simulation. It also provides information for the frequency domain pattern creation from this simple representation. This type of characterization provides the following advantages:
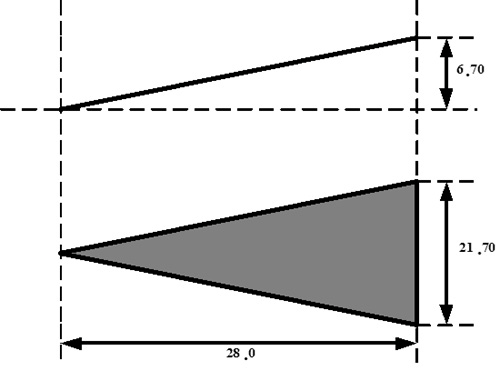
We present simple models for several antennas, providing insight into the operation of the antennas for UWB applications. Only seven poles are typically required to model these antennas. Pole modeling of the monopole antenna is also demonstrated to show the results for a narrowband structure. The monopole requires six to 39 poles to accurately model the antenna, depending on the region of interest. The most complete model is presented for the Vivaldi antenna. The poles and residues are obtained for the azimuth plane (Vivaldi antenna E-plane) for all 360 degrees in five-degree increments. The Vivaldi antenna frequency-domain patterns were obtained using a 17-pole model from the transient responses at different azimuth angles. The frequency-domain patterns obtained agree well with the measurements obtained using a near-field scanner. Pole Modeling of Antenna SystemsThe modeling is based on the measurements using the vector network analyzer, HP8510, as shown in Figure 4.5. The basic concept uses the form of (4.44) given by Equation 4.59 The realized effective length includes the impedance mismatch not normally included in effective-length definitions. The antennas are assumed to be line-of-sight (LOS) with multipath components in the response deleted using time gating. The link measurements combine the effects of the transmit/receive antennas and the channel as indicated in (4.59). The time domain waveform of the single-antenna, realized effective length can be obtained by using two identical antennas or a known reference antenna. After the realized effective length of the single antenna is obtained, one can obtain a pole and residue approximation using Prony's method [16] or an equivalent pole and residue extraction technique, such as the matrix pencil method [17]. The pole-residue model was introduced with a theoretical electromagnetic basis by Carl Baum [18] and was used to develop approaches to target identification and related modeling issues in the 1970s and 1980s. This modeling approach uses the poles of the antenna to describe the realized effective length and the residues to represent the angular information. The model is useful in both time and frequency domains with the same set of parameters. The representation of the realized effective length in terms of poles and residues is given in the frequency domain as Equation 4.60 and in the time domain as Equation 4.61 Representations (4.60) and (4.61) indicate that after the poles sa and residues Ra (q, f) are determined, it is straightforward to obtain the realized effective length in both time and frequency for any arbitrary direction. The factor N represents the total number of poles used. The poles come in complex-conjugate pairs or negative-real values in order to represent a real function. It is important to note that the poles are independent of the direction, with all the directional information contained in the residues. Thus, the same set of poles is present in all the directions. In order to obtain the antenna frequency-domain pattern, one only needs to sum all the residue contributions as in (4.60). Likewise, the time-domain pattern information is obtained from (4.61). This type of modeling provides a convenient way of describing the antenna system because only pole and residues are required to have an antenna characterization, providing a minimal form of representation for the antenna. The reflection response can also be computed in terms of the poles. The poles and residues of the transient waveform can be obtained by variations of Prony's method [16]. The expression of (4.61) does not take into account the early transient response of the antenna during pulse excitation, but only the damped, characteristic impulse response of the antenna. The transient response of the antenna consists of an early time portion that represents the excitation and a late time transient that represents the antenna characteristics. For the antennas measured, the early time duration was less than 50 ps. This time is usually associated with the finite frequency window of the measurement system. The Vivaldi antenna appears to have an early time delay of about 533 ps. However, the 533 ps corresponds to the time that is required for the excitation pulse to reach the phase center of the antenna from the reference plane with additional radiation from the feed region of the antenna. Another issue with Prony's method is the possible existence of a Nyquist pole that appears as a result of the pole-residue extraction in a sampled data system. A Nyquist pole has an imaginary part corresponding to the Nyquist sampling frequency of the data. The Nyquist pole should be split with a conjugate mate for the corresponding residue value in the model. For the TEM horn and biconical antenna models, the complex conjugate of the Nyquist pole is added to the model with a corresponding split in the residue values. Biconical Antenna ModelTwo biconical antennas were measured in a boresight, line-of-sight link. The distance between the reference planes was 1.7700 meters. The distance response of the LOS link was removed in (4.45) to obtain the square of the effective length. A square root gives the effective length after some care in unwrapping the phase. From the single response of the biconical antenna, Prony's method was applied to obtain the poles and residues of the antenna system. Figure 4.20 shows the phase and amplitude response of the single biconical antenna (dashed) and the Prony's method approximation (solid). The time domain window used to obtain the response of the single biconical antenna was 10.0 ns. The window used in Prony's method was 0.45 ns. Figure 4.20. The Six-Pole Model of the Biconical Antenna (Solid) Compared with Measured Frequency Domain Data Using a 2.5 ns Time Domain Window (Dashed).SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 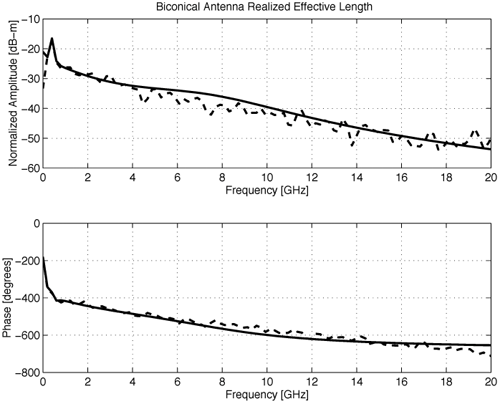 Figure 4.21 shows the pole structure and the realized effective length of the biconical antenna in the time domain for a six-pole model. The main pulse shape is preserved with the six-pole model. Figure 4.21. The Six-Pole Model Structure and Resulting Time Domain Waveform for the Biconical Antenna.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 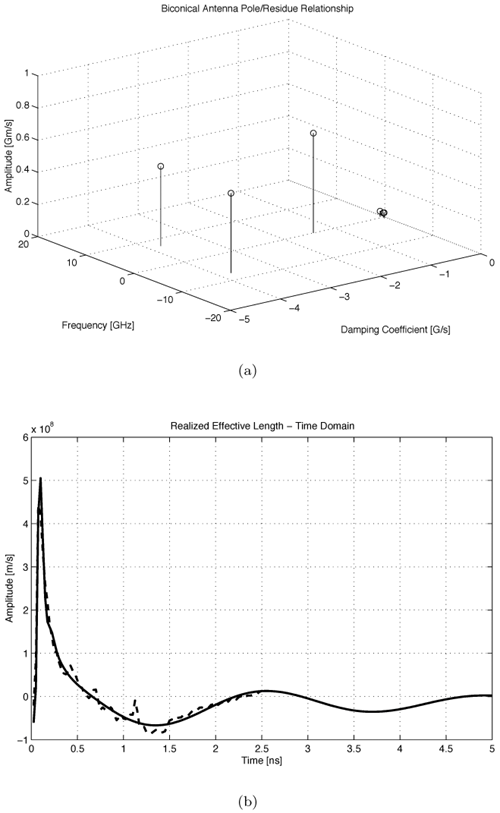 Monopole Antenna ModelThe response of the single monopole was obtained by using the TEM horn antenna of Figure 4.13 as a reference. The measurements were done by using the 4 x 4 ft ground plane in order to eliminate problems caused by a balun structure and effects caused by an edge of the finite ground plane required for monopole type structures. The distance between the reference planes of the monopole and the TEM horn antenna was 1.3500 meters. Figure 4.22 shows the amplitude and phase of the 39-pole model of the monopole antenna compared to measured, frequency-domain data. Figure 4.22. The 39-Pole Model of the 1.0 GHz Monopole Antenna (Solid), Compared to Measured Frequency Domain Data Using a 2.5 ns Time Domain Window (Dashed).SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 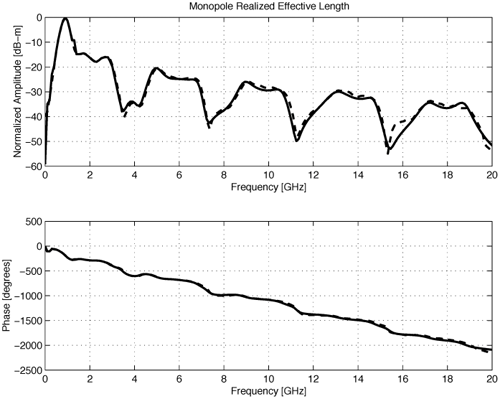 The 39-pole model is in good agreement with the measured data. The monopole antenna exhibits many resonant frequencies, as the amplitude response shows. Thus, a monopole antenna requires a large number of poles for a complete characterization, indicating that resonant-antenna system models require a larger number of poles compared to wideband antenna systems. The pole structure and the time-domain, realized effective length of the monopole are shown in Figure 4.23. The poles appear structured in three layers, as has been found previously by several authors [19]. It is expected that the first pole layer has the most dominant effect on the antenna system. The realized effective length in the time domain is in good agreement with the 39-pole model. Figure 4.23.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 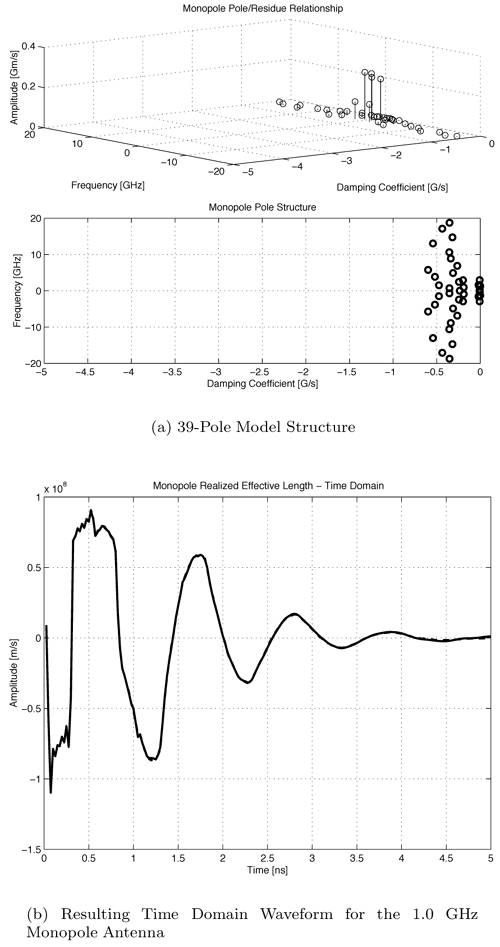 It is also interesting to consider the results obtained from reducing the number of poles used to represent such a narrowband antenna. Figure 4.24 shows the frequency and time responses of the antenna with only six poles. The data provides a good fit in the time domain, which is dominated by the low-frequency pole, but does not match the higher frequencies well. Indeed, the poles shown in Figure 4.25 are basically the dominant poles of the 39-pole model. Figure 4.24. The Six-Pole Model of the 1.0 GHz Monopole Antenna (Solid) Compared to Measured Frequency and Time Data Using a 2.5 ns Time Domain Window (Dashed).SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission.  Figure 4.25. The Poles for the Six-Pole Model of the 1.0 GHz Monopole.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 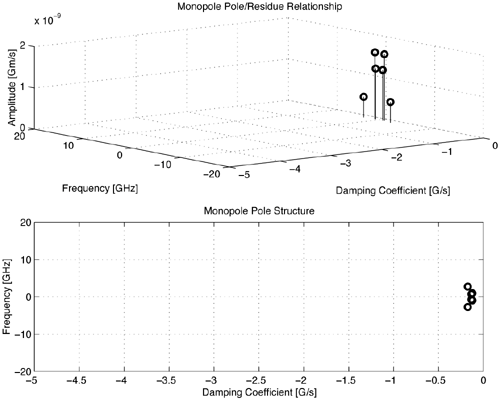 Vivaldi Antenna Model and Frequency-Domain Antenna PatternsIt is possible to obtain the frequency domain patterns from the pole-residue antenna model. The Vivaldi antenna was used to prove this concept. The results show that after the residues and poles are known, the frequency domain pattern can be obtained for any arbitrary frequency. In order to obtain the frequency domain pattern, one needs to obtain residues for different antenna orientations. The Vivaldi antennas were measured using the setup shown in Figure 4.26. The distance between the reference planes of the measured Vivaldi antennas was 2.0625 meters. The antennas were measured in a VTAG laboratory room using the vector network analyzer. One antenna was stationary while the other antenna was rotated. The measurements were taken in the azimuth plane (Vivaldi antenna E plane) at 5-degree increments for all 360 degrees. For complete characterization one needs to measure a complete sphere surrounding the antenna, but generally an azimuthal measurement is adequate. The concept is demonstrated by a measurement in a single plane. Figure 4.26. The Measurement Setup.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. The accurate description of the Vivaldi antenna requires a 17-pole model. However, the 17-pole model indicates that eight frequencies dominate the antenna response. Figure 4.27 shows the amplitude and phase of the measured (dashed) and 17-pole model approximation (solid) of the Vivaldi antenna response. The model agrees very well with the measured results. The Vivaldi antenna shows a "hybrid" type of operation compared to the monopole and TEM horn antenna models. A resonance occurs at low frequencies, yet the response moves toward a constant gain response at higher frequencies. Figure 4.27. The 17-Pole Model of the Vivaldi Antenna (Solid) Compared to Measured Frequency Domain Data Using a 2.5 ns Time Domain Window (Dashed).SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 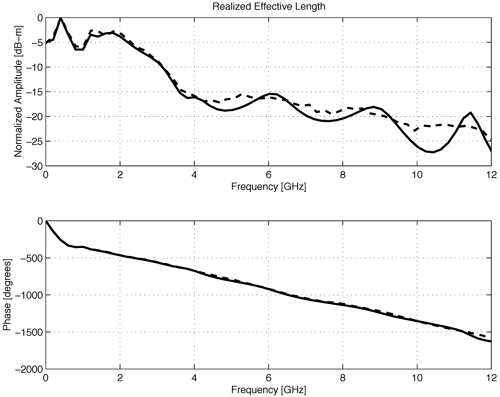 Figure 4.28a shows the pole structure of the Vivaldi antenna. The pole structure shows that it is possible to reduce the number of poles by eliminating poles with high damping coefficients. However, one needs to take the residues associated with a particular pole into consideration. Large amplitude residues can have a pronounced impact on the model even if the damping coefficients are high. The pole reduction has been pursued and a substantial reduction in the number of required poles is possible. The time-domain match of Figure 4.28b shows that the model approximates the early part of the waveform (<0.5 ns) very accurately. Figure 4.28. The (a) 17-pole Model Structure and (b) Resulting Time Domain Waveform for the Vivaldi Antenna.SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission.  After all the residues for the azimuth plane are obtained, one can reconstruct frequency domain patterns for any arbitrary frequency based on (4.60). The pattern is the combination of all the residues and poles. The poles used in the pattern calculations in Figure 4.29 are the poles obtained from the boresight direction. It may be necessary to evaluate the poles for different antenna directions in order to ensure a correct set of poles to represent the antenna system. The association of the poles from multiple directions can be used to reduce experimental error in the pole extraction. As an alternative, the poles obtained from the boresight can be used for all directions, with care taken to not miss some poles that cannot be represented adequately at the boresight. The poles obtained from the boresight measurement of the Vivaldi antenna provide a good choice of poles. Figure 4.29. The Normalized Frequency Domain Patterns (E Plane) for the Vivaldi Antenna (Dashed: Model; Solid: Near-Field Measurements).SOURCE: S. Licul, "Unified Frequency and Time-Domain Antenna Modeling and Characterization," Ph.D. dissertation [7]. © S. Licul, 2004. Used by permission. 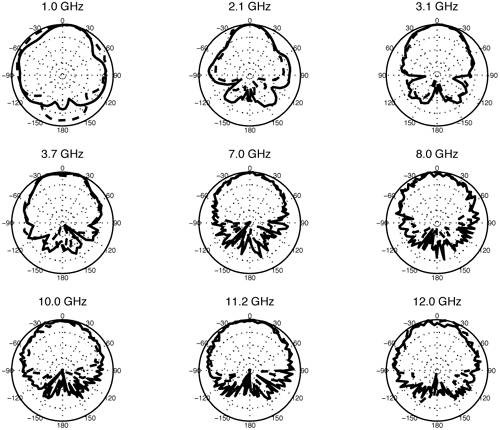 The field patterns, shown in black, were obtained by using the antenna in an anechoic chamber. The antenna was mounted on a positioner consisting of a metal mast surrounded by absorber. The measurements partially reflect from the positioner and are blocked by the positioner when the antenna is directed away from the test probe. Indeed, it is possible to develop a useful minimal model representation for an antenna system. Pole modeling of antenna systems provides complete frequency and time domain antenna characterization with a minimal representation (minimal data set required to represent an antenna). The corresponding model can be used with channel models in order to predict the received time-domain or frequency responses. The antenna pole structure is the same regardless of the antenna orientation. The residues are obtained from the transient responses at different angles. 4.2.6. Transient Responses of ScatterersThe singularity expansion method (SEM) [20] allows characterization of canonical objects in terms of poles and residues from a measured time domain system response. The data collected through transient measurements were postprocessed using Prony's algorithm to obtain a pole response. The models considered include canonical structures of a sphere, cylinder, and straight edge of different dimensions. The data were recorded for the scatter data from these canonical objects based on equivalent time-domain measurements using an HP8510. Measurement Setup Using Planar TEM Horn AntennasTwo sets of measurements were conducted to characterize canonical objects, one using planar TEM horn antennas with a ground plane and one using wideband Vivaldi antennas without a ground plane. A 4 x 4 feet square ground plane was used with two planar TEM horn antennas mounted at diagonal corners of the ground plane. An initial unobstructed line-of-sight measurement was conducted with the horns directed at each other, which was used to deconvolve the effects of the antennas. Later, the antennas were oriented toward a third corner, as shown in Figure 4.30. Measurement data was recorded with the antennas pointed toward the third corner with no object. This reference response was used to subtract the effect of the surrounding environment and the direct path. The objects were placed at a distance of 28 inches from the antenna feed point. The edge of the ground plane was covered with absorber to prevent diffraction from the edge, as well as to prevent scattering from the surrounding environment. Figure 4.30. Scatter Measurement Setup Using Planar TEM Horn Antennas.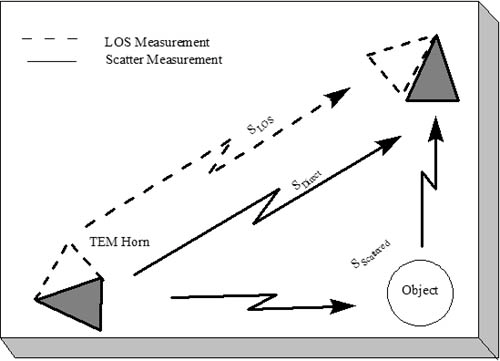 The scattered data was postprocessed to subtract the effect of the surrounding region and the direct path, as well as to deconvolve the effects of the antennas used for the measurement. The first canonical object used was a hemisphere of six inches in diameter. The image from the ground plane allowed the hemisphere to behave like a sphere in free space. The transient response from the hemisphere is shown in Figure 4.31. The response consists of a specular component followed by an apparent resonant component. The specular reflection is inverted for positive pulse excitation. Figure 4.31. Transient Scatter Response of a Hemisphere of Six-Inch Diameter.SOURCE: R. M. Buehrer, W. A. Davis, A. Safaai-Jazi, and D. Sweeney, "Ultra-wideband Propagation Measurements and Modeling," [22]. © Mobile and Portable Radio Research Group, 2004. Used by permission.  The frequency response of the hemisphere is shown in Figure 4.32. Periodic nulls occur with a staggered stair-like response. The periodic frequency of the ringing observed in Figure 4.31 seems evident from the peak observed at 700 MHz. The nearly flat high frequency response illustrates the smooth specular component. The extracted complex poles for the hemisphere are shown in Figure 4.33. A total of 25 pairs of complex-conjugate poles were extracted and illustrate the absence of double poles, with the two poles of about 700 MHz dominating the resonate part of the response. Figure 4.32. Frequency Scatter Response of a Hemisphere of Six-Inch Diameter Using Planar TEM Horn Antenna.SOURCE: R. M. Buehrer, W. A. Davis, A. Safaai-Jazi, and D. Sweeney, "Ultra-wideband Propagation Measurements and Modeling," [22]. © Mobile and Portable Radio Research Group, 2004. Used by permission. 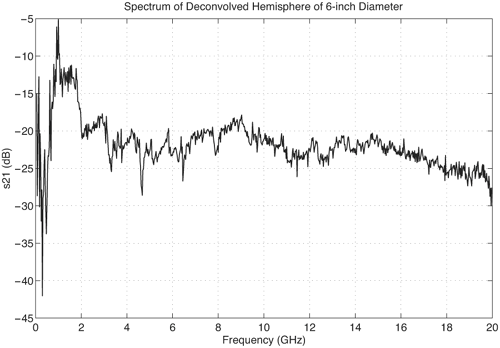 Figure 4.33. Pole Plot of a Hemisphere of Six-Inch Diameter.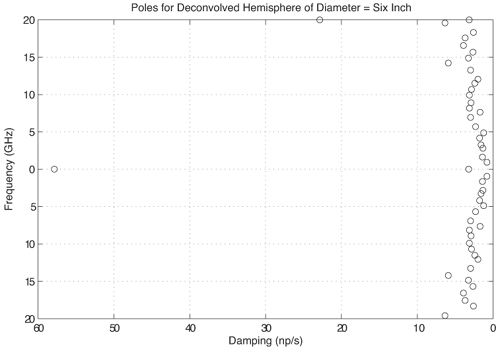 Additional plots for other canonical objects are also shown in Figures 4.344.36. These plots include a cylinder four inches in diameter, the edge of a cube of side length 90 mm, and the edge of a 4 feet x 4 feet conducting surface. The study of such canonical shapes is expected to provide additional information into the performance of multipath scattering in a UWB environment. Most of the objects considered demonstrate both a resonant and a specular response. A large edge, such as might be expected in a doorway or large building, is not expected to have the same resonant response, but a response characteristic of diffraction of an edge or corner. Though this research is in its infancy, it provides insight into the variations of the responses that may be needed for appropriate modeling of transient and frequency multipath scattering. Figure 4.34. Transient Scatter Response of a Cylinder of Four-Inch Diameter.SOURCE: R. M. Buehrer, W. A. Davis, A. Safaai-Jazi, and D. Sweeney, "Ultra-wideband Propagation Measurements and Modeling," [22]. © Mobile and Portable Radio Research Group, 2004. Used by permission. 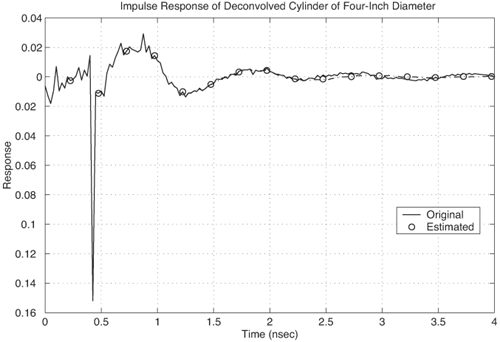 Figure 4.35. Transient Scatter Response of an Edge from a Cube of 90 mm Side Length.SOURCE: R. M. Buehrer, W. A. Davis, A. Safaai-Jazi, and D. Sweeney, "Ultra-wideband Propagation Measurements and Modeling," [22]. © Mobile and Portable Radio Research Group, 2004. Used by permission. 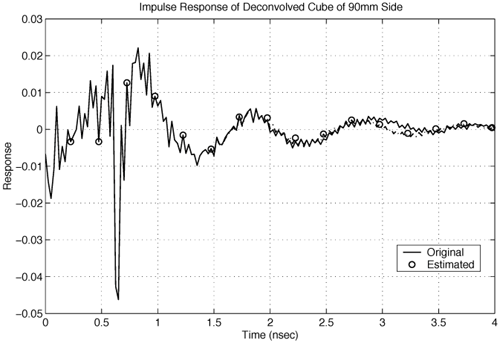 Figure 4.36. Transient Scatter Response of an Edge (Four Feet).SOURCE: R. M. Buehrer, W. A. Davis, A. Safaai-Jazi, and D. Sweeney, "Ultra-wideband Propagation Measurements and Modeling," [22]. © Mobile and Portable Radio Research Group, 2004. Used by permission. 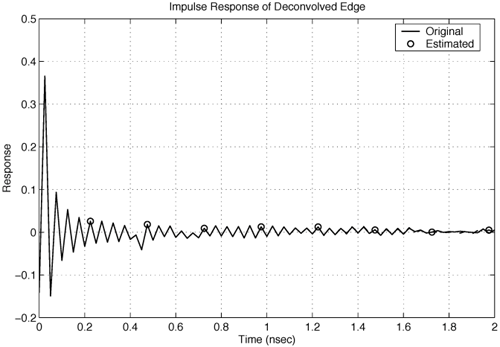 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
EAN: 2147483647
Pages: 110