JOIN
|
|
For this operator many definitions have been proposed, with more or less little differences. We briefly discuss natural join, identity-based join, value-based join, S-join, S (f)-join and star-join:
Natural join: This operator was proposed for multidimensional aggregate data in Cabibbo & Torlone (1998). If E1 and E2 are MADs (or f-expressions) over the schema [A1, A2, …, Ak, Ak+1, …, An] → [M1, M2, …, Mm] and [A1, A2, …, Ak, A'k+1, …, A'n] → [M'1, M'2, …, M'm], respectively, that is, having A1, A2, …, Ak as common attributes (defined over the same level) and no common measure, then E1 ![]() , E2 is a MAD with schema over the attributes A1, A2, …, Ak, Ak+1, …, An, A'k+1, …, A'n and measures M1, M2, …, Mm, M'1, M'2, …, M'm. The result has an entry for each pair of entries in the two MADs with the same values in the common attributes. The corresponding measures are the juxtaposition of the measures in the original entries.
, E2 is a MAD with schema over the attributes A1, A2, …, Ak, Ak+1, …, An, A'k+1, …, A'n and measures M1, M2, …, Mm, M'1, M'2, …, M'm. The result has an entry for each pair of entries in the two MADs with the same values in the common attributes. The corresponding measures are the juxtaposition of the measures in the original entries.
Identity-based join: This operator was proposed in Pedersen & Jensen (1999) and Pedersen, Jensen, & Dyreson (2001), and is used to combine information from several MADs. It produces a new fact type which consists of pairs from the old fact type, and a new set of dimension types which is the union of the old sets. The set of facts is the subset of the cross-product of the old sets of facts where the join predicate p holds. For p equal to fl = f2, fl ≠ f2 and true, the operation is an equi-join, non-equi-join, and Cartesian product, respectively. For this instance, the set of dimensions is the set-union of the old sets of dimensions, and the fact-dimension relations relate a pair to a value if one member of the pair was related to that value before.
Then, given two MADs, s1 and s2, and a predicate p(fl,f2) ∊ (fl = f2, fl ≠ f2, true}, we define the identity-based join > as:

Value-based join: This operator was proposed in Pedersen, Jensen, & Dyreson (2001). It is a join of two MADs on common dimension values, by combining Cartesian product (a special case of the identity-based join), selection, and projection. Natural join is another special case of this operator, where the selection predicate requires that values from the "matching" dimensions should be equal, followed by projecting "out" the duplicate dimensions. In practice, performing this operator on the common dimensions of two MADs means carrying out the drill-down operation from one MAD to another MAD.
S-join: This operator carries out a juxtaposition of two MADs, T1 and T2, which have the same descriptive space (S1=S2 where S1: <X1, Y1>, etc. ), but in which the corresponding definition domains can be different (dom(X1) = <x1, x2, x3> and dom(X2) = <x1, x3, x4, x5>, etc.), and have as equal summary type (which has to be "summable") and the same fact. For example, let T1 and T2 be two given MADs shown in Figure 23.
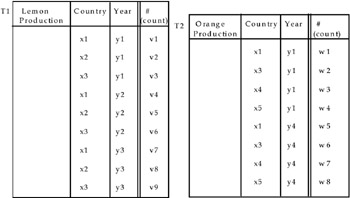
Figure 23
The conditions mentioned above require the same descriptive space (in this case, "nations" and "year"), the same summary type (in this case, "count"), and the same described fact (in this case, "production of fruit.") Applying the S-join, we obtain MAD T3 in Figure 24.
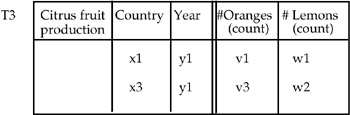
Figure 24
The alternative could be that to obtain MAD T4 of Figure 25. In this second case, MAD T4 could be a complex MAD (see the ADAMO model in Chapter 1), whose summary values could have different summary types.
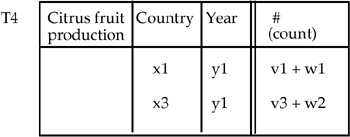
Figure 25
The conditions mentioned above require the same descriptive space (in this case, "country" and "year"), the same summary type (in this case "count"), and the same described fact (in this case "citrus fruit production").
Applying the S-join operator we obtain MAD T3 in Figure 24.
Note that T3 is a composite table, where the two component MADs have the same dimensions but different subjects. Because these subjects are "part-of" of the higher level in the primitive hierarchy "Citrus fruit ← <Oranges, Lemons,…>," we can apply the roll-up operator to this hierarchy (treating the measure as another dimension), to obtain the MAD in Figure 25.
S(f)-join: A variant of the previous operator is S(f)-join. In this case the only condition (verifiable only by the user) which has to be satisfied is that the described fact must be the same. This means that both the descriptive spaces (S1 and S2) and their definition domains can be different (dom X1 and dom X2), and (like the second case of the S-join) their summary types can also be different. For example, let T5 and T6 be two MADs shown in Figure 26.
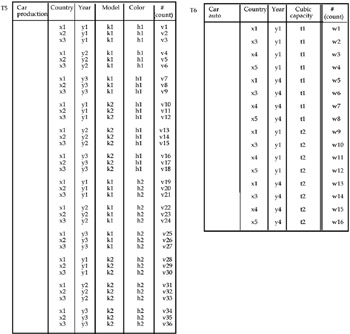
Figure 26
In this case the two descriptive spaces are different (even if they have a common subset, "nations" and "year"), and the cardinality of each MAD is also different (4 and 3, respectively). In order to apply the operator S-join, a "normalization" of the two descriptive spaces has to be made, obtaining only one schema. This means performing a slice operation (in this case, a P-slice), and possibly a roll-up operation (in case of the presence of hierarchies along the same dimension).
In the case in Figure 26 we have:
Dice T3 (Model, Color)
Dice T4 (Cubit capacity)
Therefore, we proceed as in the previous case, because no hierarchies are present in all the remaining dimensions.
Notice that every time a normalization is performed, a note has to be produced (which explains which dimension has become "implicit").
In the case in Figure 26, this note will contain information regarding what model (k1 and k2) and what colors (h1 and h2) refer to the summary data. If we delete model and color in T5, the summary values which refer to the pair x1-y1, that is, v1, v10, v19, and v28, are summed (obviously, we suppose that they are summable), as well as the summary values which refer to the pairs x1-y2, x1-y3, and so on and analogously for MAD T6.
If, instead, the summary values are not summable (average, max, min, etc.), the S(f)-join has to be applied, where f represents the function which has been applied to microdata during the aggregation process which produced the aggregate data.
Obviously, it prefigures that we have all the microdata of the initial database at our disposal or, at least, the "basic" microdata (count and sum) necessary to the application of the formula (relative to the aggregation function) leads to aggregate data. The final result of the P-slice operation on the MAD in Figure 26 is shown.
In the case in which the summary values are summable, in Figure 27, the result of the S-join operation is shown in Figure 28.
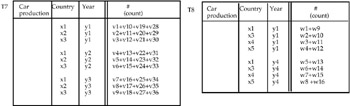
Figure 27
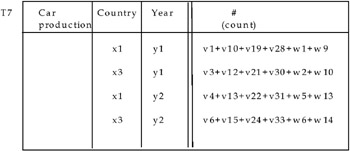
Figure 28
Star-join: A star join, as described in Klug (1982), is merely a selection on the dimensions, usually combined with an aggregate formation with a given aggregate function on a set of category types.
|
|
EAN: 2147483647
Pages: 150