MULTIDIMENSIONAL AGGREGATE DATA

Most of the existing models for aggregate data represent a MAD as a mapping between category and summary attributes. The analysis of the aggregation process shows aggregate data in a new perspective. A MAD represents a functional link between aggregation sets and summary values, rather than between tuples of category attribute instances and summary values. In this framework the category attributes and the corresponding instances express the constraints which univocally characterize the single aggregation sets.

Now we can formally define multidimensional aggregate data (MAD) and the multidimensional aggregate data structure (MADS). In this three different data structures for multidimensional aggregate data were proposed: simple, complex, and composite MAD (referred to as statistical object, SO, in that paper). The aggregation sets of an aggregation process can often be represented simply by cross-intersecting the classification and union sets of the explicit and implicit attributes respectively. In such cases the aggregation process is represented by a simple MAD.

Definition 12 A simple MAD is a conceptual multidimensional aggregate data defined by the six-tuple , where:

• P is the fact name described by the MAD. Through the mapping φ, P identifies a fact universe .

• N is the numerical domain where the summary attribute is defined 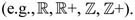Note that the summary attribute is actually defined on an extension of N, namely on N ∪ {‘N.A.’} ∪ {‘S.Z.’}, where ‘N.A.’ is for not available and ‘S.Z.’ for structural zero, as defined in Malvestuto (1993).

• f is the type of aggregation function (e.g., count, sum, average).

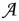• is the set formed by the two subsets ∊ and I, where:

  • - ∊ is the set of explicit category attributes, each of them with its corresponding ordered instance domain:

    

    (M represents the number of explicit category attributes, while P_j (j = 1,…, M) the number of instances of the j-th attribute).

  • - I is the set of implicit attributes, each of them with its corresponding unique instance of the definition domain:

    

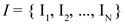
    (N represents the number of implicit attributes).

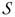• is the subject of the MAD, i.e., the "what is" of the cell value, the instance of the measure.

• s is a set of (P_{(j=1, M)} P_j) summary values in bijective correspondence with the aggregation schema of the i-th simple MAD.

Definition 13 A simple MADS is a logical multidimensional aggregate data structure defined by the six-tuple where:

• P,

• N, and

• f have the same meaning as the previous definition.

• is the ordered set formed by the two subsets and where:

  • - is the ordered set of explicit category attributes, each of them with its corresponding ordered instance domain:

    

    (M represents the number of explicit category attributes, while P_j (j = 1,…, M) the number of instances of the j-th attribute).

  • - I has the same meaning as the previous definition.

• s is an ordered set of ∏_(j=1,M) P_j) summary values in bijective correspondence with the aggregation schema A_ij of the simple MADS.

For example, a simple MADS is the table shown in Figure 4.

Definition 14 A Complex MAD is a conceptual multidimensional aggregate data in which one or more dimensions is partitioned into two or more subsets, each of which is "classified by" different attributes. This situation can produce a union of subMADS, each of them with a possible different cardinality.

Analogously, a Complex MADS has the same definition, with the obvious difference of the ordered sets e and s.

In Figure 5 an example of this situation is shown. In this case the MADS has to be split into two (or more) different MADS.

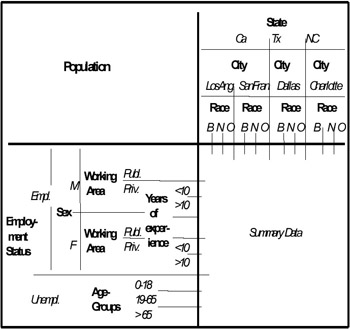
Figure 5: A Complex MADS

A subtle distinction has to be made between the concept of multidimensionality and that of polidimensionality. The former refers to a data structure in which measured data is described by different (two or more) parameters which define a multidimensional descriptive space. The latter refers to a descriptive space in which a category attribute has, for example, one part of its definition domain classified by one or more other category attributes, A, B, …C, while the other part is classified by one or more different category attributes, E, F, …H. Note that the number of the first and the second group of category attributes can be different. For example, with regard to the MADS of Figure 5, which is a typical example of polidimensional MADS, the category attribute "Employment Status" has its instance "Employed" classified by "Sex," "Working Area," and "Years of Experience," while the other instance "Unemployed" is classified by "Age Groups." This means that such a MADS will have one part with the three common dimensions "State-City," "Race," and "Employment Status" (this last with the only instance "Employed"), plus the three other dimensions "Sex," "Working Area," and "Years of Experience" (i.e., with cardinality = 6), while the other part has the above-mentioned three common dimensions (with the only instance "Unemployed" of the dimension "Employment Status"), plus the other dimension "Age Groups" (i.e., with cardinality = 4).

A MAD (or a MADS) may collect data from two or more aggregation processes (composite MAD or MADS). Then:

Definition 15 A composite MAD is a conceptual multidimensional aggregate data defined by the set {a₁, a₂,…, a_S}, where each element a_j is a complex (possibly simple) MADS, and in which different summary types generally appear.

Analogously, a composite MADS is a MADS defined by the ordered set {a₁, a₂,…, a_S} as defined in the previous definition.

This means that this type of MAD (or MADS) is obtained by the union of two (or more) MAD (MADS) in which the fact described was the same, but the summary type was different. This union is performed only if a common dimension, along which such a union is made, exists.

For example, in Figure 6 an example of composite MADSs (represented by a table) is shown. Also in this case the MADS can be split into two (or more) MADSs, each of them with a unique summary type. Obviously, we can have the combination of the two situations, i.e., a complex-composite MADS, as shown in Figure 7.

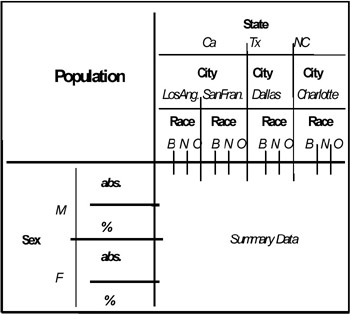
Figure 6: A Composite MADS

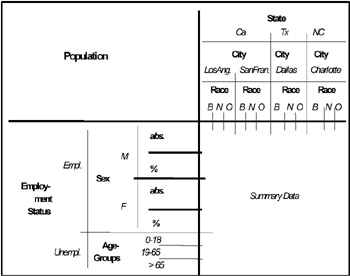
Figure 7: A Complex-Composite MADS

In Malvestuto (1993) two statistical objects are defined as being "homogeneous" if they refer to the same summary variable and to exactly the same population, i.e., if they have been obtained by applying the same aggregation function, and the collection of units of observation (microdata) involved is exactly the same. Malvestuto makes the assumptions that 1) the category attributes partition the population and that 2) the aggregation function is additive. He shows that, under these hypotheses, a collection of homogeneous statistical objects can be queried as if they were actually a single, higher dimensional object and that the set of answerable queries can be larger, compared to the one resulting from querying the single statistical objects separately. Moreover, important results on the answerability and evaluability of a query are obtained. Unfortunately, determining homogeneity is generally rather difficult, since there may be thousands of populations in an aggregate database, and each time we want to insert a new statistical object or query the database, we need to know the name of the population of interest or to carefully browse a long list of population names.