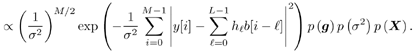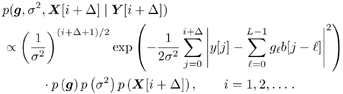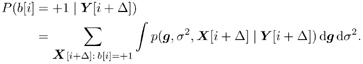8.2 Bayesian Signal Processing
8.2.1 Bayesian Framework A typical statistical signal processing problem can be stated as follows : Given a set of observations Example 1: Equalization Suppose that we want to transmit binary symbols b [1], b [2], ..., b [i] Equation 8.1 where In the Bayesian approach to statistical signal processing problems, all unknown quantities [i.e., ( X , Q )] are treated as random variables with some prior distribution described by a probability density p ( X , Q ). The Bayesian inference is made based on the joint posterior distribution of these unknowns, described by the density Equation 8.2 Note that typically, the joint posterior distribution is completely known up to a normalizing constant. If we are interested in making an inference about the i th component x i of X [i.e., we wish to compute E { h ( x i ) Y } for some function h ( ·)], this quantity is given by Equation 8.3 Equation 8.4 where For an introductory treatment of the Bayesian philosophy, including the selection of prior distributions, see the textbooks [51, 136, 248]. An account of criticism of the Bayesian approach to data analysis can be found in [33, 422], and a defense of the Bayesian choice can be found in [419]. 8.2.2 Batch Processing versus Adaptive ProcessingDepending on how the data are processed and on how the inference is made, most signal processing methods fall into one of two categories: batch processing and adaptive (i.e., sequential) processing. In batch signal processing , the entire data block Y is received and stored before it is processed, and the inference about X is made based on the entire data block Y . In adaptive processing , on the other hand, inference is made sequentially (i.e., online) as the data are being received. For example, at time t , after a new sample y t is received, an update on the inference about some or all elements of X is made. In this chapter we focus on optimal signal processing under the Bayesian framework for both batch and adaptive processing. We next illustrate batch and adaptive Bayesian signal processing, respectively, using the equalization example above. Example 1: Batch Equalization Consider the equalization problem mentioned above. Let Equation 8.5 Equation 8.6 The a posteriori probabilities of the transmitted symbols can then be calculated from the joint posterior distribution (8.6) according to Equation 8.7 Equation 8.8 Clearly, the direct computation in (8.8) involves 2 M -1 multidimensional integrals, which is certainly infeasible for most practical implementations in which M might be on the order of hundreds. Example 2: Adaptive Equalization Again consider the equalization problem above. Define Equation 8.9 An online symbol estimate can then be obtained from the marginal posterior distribution Equation 8.10 Again we see that direct implementation of the optimal sequential Bayesian equalization above involves It is seen from the discussions above that although the optimal (i.e., Bayesian) signal processing procedures achieve the best performance (i.e., the Bayesian solutions achieve the minimum probability of error on symbol detection), they exhibit prohibitively high computational complexity and thus are not generally implementable in practice. The recently developed Monte Carlo methods for Bayesian computation have provided a viable approach to solving many such optimal signal processing problems with reasonable computational cost. 8.2.3 Monte Carlo MethodsIn a typical Bayesian analysis, the computations involved in eliminating the missing parameters and other unknown quantities are so difficult that one has to resort to some numerical approaches to complete the required summations and integrations. Among all the numerical approaches, Monte Carlo methods are perhaps the most versatile, flexible, and powerful [275]. Suppose that we can generate random samples (either independent or dependent) from the joint posterior distribution (8.2); or we can generate random samples from the marginal posterior distribution p ( X Y ). Then we can approximate the marginal posterior p ( x i Y ) by the empirical distribution (i.e., the histogram) based on the corresponding component in the Monte Carlo sample (i.e., x (1) i , x (2) i ,... x ( n ) i ) and approximate the inference (8.4) by Equation 8.11 As noted in Section 8.1, most Monte Carlo techniques fall into one of the following two categories: Markov chain Monte Carlo methods, corresponding to batch processing, and sequential Monte Carlo methods, corresponding to adaptive processing. These are discussed in the remainder of this chapter. |
EAN: 2147483647
Pages: 91
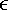 {+1, -1}, through an intersymbol interference (ISI) channel whose input “output relationship is given by
{+1, -1}, through an intersymbol interference (ISI) channel whose input “output relationship is given by