Chapter 3: The Brennan and Schwartz Model
Brennan and Schwartz (BS) [ 10 ] challenge the primary assumption of many models. That is: all information about future interest rates is contained in the current instantaneous short- term interest rate and hence the prices of all default-free bonds may be represented as time-dependent functions of this instantaneous rate only. They point out that this is not an accurate representation of reality and propose an interest rate model based on the assumption that the whole term structure can be expressed as a function of the yields of the longest and shortest maturity default-free bonds.
They incorporate the assumption that the long-term rate of interest contains information about future values of the short-term interest rate. This long-term interest rate is the second, exogenously specified variable and the term structure between the short- and long-term interest rates is modelled as a function of these two rates. Other models derive the whole term structure, and hence the long-term rate of interest as a function of the short-term interest rate.
3.1 The generic model
Let
| r ( t ) - | instantaneous rate of interest, |
| l ( t ) - | long-term interest rate represented by the yield on a consol bond paying a continuous dividend. |
BS [ 10 ] assume r ( t ) and l ( t ) to follow a joint Gauss-Markov stochastic process of the general form:
where t is the current time and
| dz 1 , dz 2 - | represent Wiener processes [1] , |
| ² 1 ( · ), ² 2 ( · ) - | are the expected, instantaneous rates of change of r and l respectively, |
| · 2 1 ( · ), · 2 2 ( · ) - | are the instantaneous variances of r and l respectively, |
| - | instantaneous correlation between the unanticipated changes in r and l i.e. dz 1 dz 2 = dt |
| [1] As usual, the Wiener processes dz 1 and dz 2 have the following characteristics:
This last point is not technically precise, but is used as an informal representation of the discrete time formulation: where z is some Wiener process and t k , t k+1 are consecutive points in time. See[ 49 ]. | |
Let B ( r, l, ) be the price of a zero coupon bond with maturity date T = t + and unit maturity value. Since this bond price is a function of the two rates of interest and time to maturity , we may apply Ito's Lemma to derive the equation of the stochastic process for the bond price [2] :

and hence the bond price process may be written as
where
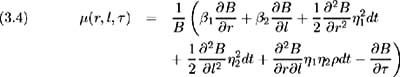
An arbitrage argument is applied to derive the equilibrium relationship between bonds of various maturities. This relationship takes the form of a partial differential equation which places constraints on the risk premia of bonds of various maturities. We consider a portfolio of three bonds of different maturities. This allows us to hedge away the uncertainty associated with both stochastic variables , i.e. r and l .Let:
| P - | portfolio of bonds of three different maturities, |
| x i - | amount invested in bond with maturity i , i =1, 2, 3 |
with ˆ‘ i x i = 1. Ito's Lemma is applied to derive the rate of return on the portfolio as:

This return can be made instantaneously deterministic by setting the coefficients of the Wiener processes equal to zero:
To preclude arbitrage profits, the portfolio return must be the risk-free rate of interest. Hence:
that is:
Equations (3.5), (3.6), (3.7) form a system of three linear, homogeneous equations in three unknowns. This system is consistent only if:
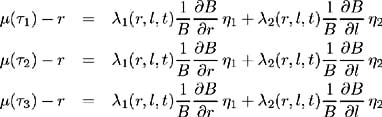
and hence this relationship holds for any bond maturity , and may be written as:
The functions » 1 ( r, l, t ) and » 2 ( r, l, t ) are independent of the bond maturity. The return on a bond in excess of the risk-free rate of interest is the premium required to compensate the investor for the additional risk. Equation (3.8) expresses this instantaneous risk premium on a discount bond as the sum of two factors. These factors are proportional to the partial covariances of the bond return with the unanticipated changes in each of the two exogenous variables. These partial covariances are represented by ![]() and
and ![]() respectively. The proportionality factors » 1 ( r, l, t ) and » 2 ( r, l, t ), may be interpreted as the market prices of instantaneous and long-term interest rate risk. These market prices of risk are investor-specific and depend on the investors' utility functions.
respectively. The proportionality factors » 1 ( r, l, t ) and » 2 ( r, l, t ), may be interpreted as the market prices of instantaneous and long-term interest rate risk. These market prices of risk are investor-specific and depend on the investors' utility functions.
Substituting (3.4) into (3.8) leads to the partial differential equation for the price of a discount bond:
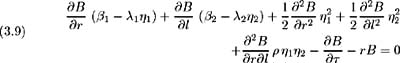
This bond pricing equation is dependent on two utility specific variables, i.e. the two market prices of risk. Assuming l to be the yield on a consol bond allows us to eliminate the market price of long-term interest rate risk » 2 ( r, l, t ). A consol bond is a bond of infinite maturity paying a continuous coupon of $1 per annum. Let V ( l ) be the price of this consol bond, then:
Applying Ito's Lemma to V ( l ) gives:
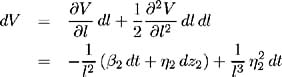
and so:
where ![]() is the partial covariance of the bond's instantaneous rate of return with the unanticipated changes in l . The instantaneous rate of return on the consol bond ¼ ( ˆ ), consists of the capital gain and the rate of coupon payment; hence:
is the partial covariance of the bond's instantaneous rate of return with the unanticipated changes in l . The instantaneous rate of return on the consol bond ¼ ( ˆ ), consists of the capital gain and the rate of coupon payment; hence:
Since we are in the risk-free world the return on the consol must be the risk-free rate of interest and hence the equilibrium risk premium relationship (3.8) must be satisfied:
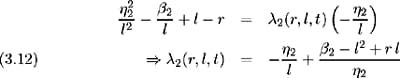
Here we have expressed the market price of long-term interest rate risk as a function of r , l and the parameters of the stochastic process of l .This allows us to reduce the number of utility-dependent factors in the bond price equation. Substituting (3.12) into the bond price equation (3.9) results in:

which is independent of the market price of long-term interest rate risk, » 2 . Applying the boundary condition B ( r, l, 0) = 1, we may solve the above equilibrium bond pricing equation for any maturity. Since the entire term structure of interest rates may be inferred from these bond prices, we conclude that the term structure, at any point in time, is a function of r , l and » 1 .
By choosing l to be the yield on a consol bond, we are able to determine the bond price independent of » 2 and ² 2 . Since the consol is a traded security, the risk associated with l may be hedged away. This is the same as the result obtained by Black and Scholes in deriving the option pricing equation, which is independent of the expected return on the underlying asset. BS [ 10 ]makethe observation that the number of investor-specific (utility-dependent) variables in the pricing equation is equal to the number of state variables (excluding time), less the number of variables for which all the partial derivatives are known. Knowledge of the partial derivatives allows the associated risk to be hedged away. This phenomenon may be demonstrated more generally as follows : the partial derivatives of the consol bond (which represents the long-term interest rate), are known. Also, since it is a traded security, it must satisfy the bond pricing equation (3.9) [ 51 ], hence:

Multiplying by ![]() and subtracting from (3.9) yields:
and subtracting from (3.9) yields:
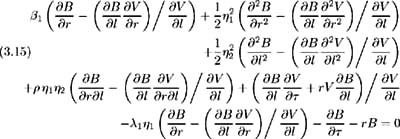
We know:

and hence (3.15) simplifies to (3.13), the bond price equation independent of » 2 . By applying the bond pricing equation to one of the underlying variables, we have reduced the number of utility-dependent parameters. The resulting model has the same estimation complexity as a one factor model, but the dynamical explanatory power of a two-factor model.
[2] Since = T ˆ’ t we have ![]()
EAN: 2147483647
Pages: 132