3.2 Specific models
3.2 Specific models
BS performed two empirical analyses ([ 10 ]and[ 11 ]) using the above general formulation of the two factor model. In both cases they assign specific functional forms to the drifts and volatilities of r and l . The free parameters in these functional forms are estimated by applying statistical methods to market data. Then, assuming the functional forms and parameter values to be the true values, they estimate the value of the market price of instantaneous interest rate risk, » 1 . To simplify the analysis, » 1 is assumed to be an intertemporal constant.
In the first analysis [ 10 ], which makes use of Canadian bond data, BS use the assumption that the excess expected rate of return on the consol bond over the instantaneous rate of interest is proportional to the degree of long- term interest rate risk (as represented in (3.12)) to solve for the expected rate of return:
where » 2 is assumed constant.
Additional assumptions are made to ensure that interest rates remain nonnegative. The standard deviations of the instantaneous changes in interest rates are assumed proportional to their current levels:

where ƒ 1 and ƒ 2 are the constants of proportionality. To determine the functional form of ² 1 ( r, l, t ), BS assume that the long-term interest rate l , contains information about future values of the instantaneous rate of interest, hence r regresses towards a function of l . That is, the assumption is made that:
From (3.1) we have:
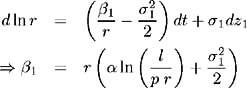
where ± is the speed of reversion of ln r to ![]() , where p is a scaling factor.
, where p is a scaling factor.
Equation (3.1) now becomes:
Applying the assumptions (3.17) to equation (3.16):
and hence (3.2) becomes:
The behaviour of the interest rates is now described by a system of nonlinear stochastic differential equations, (3.19) and (3.20). To empirically estimate the values of the free parameters, that is p , ± , ƒ 1 , ƒ 2 and » 2 ,BS linearise and discretise the system by approximating r and l with functions of ln r and ln l .
In the second analysis [ 11 ], BS use US bond data for the period 1958-1979. The joint stochastic process for the two interest rates is assumed to have the following functional form:
Again, the unanticipated changes in the interest rates are assumed to be proportional to their current levels, and the instantaneous rate is assumed to regress to the long-term interest rate, hence b 1 > 0. Allowing a 1 < 0, introduces the possibility of negative interest rates. BS acknowledge this flaw, but retain it due to its empirical tractability. They consider the resulting bond pricing model to be more significant than the properties of the linear approximation of the true stochastic interest rate process.
To obtain the drift term for the long-term interest rate, equation (3.12) was again solved for ² 2 with the additional assumption that » 2 is a linear function of the two interest rates, r and l . Therefore, as outlined in [ 45 ]:
where k , k 1 and k 2 are constants. Solving (3.12) for ² 2 and applying assumptions (3.17) and (3.23):

The system of stochastic equations (3.21) and (3.22) is then discretised so that the unknown parameters: a 1 , b 1 , ƒ 1 , a 2 , b 2 , c 2 , ƒ 2 and may be estimated from market data. Assuming these estimates are the true parameter values, » 1 is estimated. » 1 is assumed to be an intertemporal constant, an unrealistic assumption given the long time span of the market data.
The results of the empirical tests performed by BS are rather inconclusive since the inconsistencies observed can be attributed to one of four causes: model misspecification in the form of an omission of state variables , misspecification of the functional forms of the stochastic processes for r and l , market inefficiencies or measurement error. Attempts by BS to isolate the specific causes of the errors are again inconclusive.
Rebonato [ 45 ] examines the behaviour of this specific model formulation. He varies the parameters over a range of reasonable values and finds that the dynamics of the coupled system (3.21) and (3.22) tend to be quite unstable.
The long-term interest rate has a non-negligible probability of reaching very high values in a finite period of time. This instability is due to the specific functional form and parameterisation chosen by BS in the implementation of their model.
EAN: 2147483647
Pages: 132