Cryptography: Theory and Practice:Signature Schemes | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

Exercises

6.1 Suppose Bob is using the ElGamal Signature Scheme, and he signs two messages x₁ and x₂ with signatures (γ, δ₁) and (γ, δ₂), respectively. (The same value for γ occurs in both signatures.) Suppose also that gcd(δ₁ - δ₂, p - 1) = 1.

(a) Describe how k can be computed efficiently given this information.

(b) Describe how the signature scheme can then be broken.

(c) Suppose p = 31847, α = 5 and β = 25703. Perform the computation of k and a, given the signature (23972, 31396) for the message x = 8990 and the signature (23972, 20481) for the message x = 31415.

6.2 Suppose I implement the ElGamal Signature Scheme with p = 31847, α = 5 and β = 26379. Write a computer program which does the following.

(a) Verify the signature (20679, 11082) on the message x = 20543.

(b) Determine my secret exponent, a, using the Shanks time-memory tradeoff. Then determine the random value k used in signing the message x.

6.3 Suppose Bob is using the ElGamal Signature Scheme as implemented in Example 6.1: p = 467, α = 2 and β = 132. Suppose Bob has signed the message x = 100 with the signature (29, 51). Compute the forged signature that Oscar can then form by using h = 102, i = 45 and j = 293. Check that the resulting signature satisfies the verification condition.

6.4 Prove that the second method of forgery on the ElGamal Signature Scheme, described in Section 6.2, also yields a signature that satisfies the verification condition.

6.5 Here is a variation of the ElGamal Signature Scheme. The key is constructed in a similar manner as before: Bob chooses

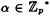to be a primitive element, a is a secret exponent (0 ≤ a ≤ p - 2) such that gcd (a, p - 1) = 1, and β = α^a mod p. The key K = (α, a, β), where α and β are public and a is secret. Let

be a message to be signed. Bob computes the signature sig(x) = (γ, δ), where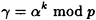

and

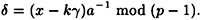
The only difference from the original ElGamal Scheme is in the computation of δ. Answer the following questions concerning this modified scheme.

(a) Describe how a signature (γ, δ) on a message x would be verified using Bob’s public key.

(b) Describe a computational advantage of the modified scheme over the original scheme.

(c) Briefly compare the security of the original and modified scheme.

6.6 Suppose Bob uses the DSS with q = 101, p = 7879, α = 170, a = 75 and β = 4567, as in Example 6.3. Determine Bob’s signature on the message x = 52 using the random value k = 49, and show how the resulting signature is verified.

6.7 In the Lamport Scheme, suppose that two k-tuples, x and x′, are signed by Bob. Let

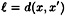denote the number of coordinates in which x and x′ differ. Show at Oscar can now sign

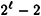new messages.

6.8 In the Bos-Chaum Scheme with k = 6 and n = 4, suppose that the messages x = (0, 1, 0, 0, 1, 1) and x′ = (1, 1, 0, 1, 1, 1) are signed. Determine the new messages that be signed by Oscar, knowing the signatures on x and x′.

6.9 In the Bos-Chaum Scheme, suppose that two k-tuples x and x′ are signed by Bob. Let

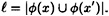Show that Oscar can now sign

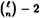new messages.

6.10 Suppose Bob is using the Chaum-van Antwerpen Undeniable Signature Scheme as in Example 6.5. That is, p = 467, α = 4, a = 101 and β = 449. Suppose Bob is presented with a signature y = 25 on the message x = 157 and he wishes to prove it is a forgery. Suppose Alice’s random numbers are e₁ = 46, e₂ = 123, f₁ = 198 and f₂ = 11 in the disavowal protocol. Compute Alice’s challenges, c and d, and Bob’s responses, C and D, and show that Alice’s consistency check will succeed.

6.11 Prove that each equivalence class of keys in the Pedersen-van Heyst Fail-stop Signature Scheme contains q² keys.

6.12 Suppose Bob is using the Pedersen-van Heyst Fail-stop Signature Scheme, where p = 3467, α = 4, a₀ = 1567 and β = 514 (of course, the value of a₀ is not known to Bob).

(a) Using the fact that a₀ = 1567, determine all possible keys

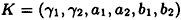
such that sig_K(42) = (1118, 1449).

(b) Suppose that sig_K(42) = (1118, 1449) and sig_K(969) = (899, 471). Without using the fact that a₀ = 1567, determine the value of K (this shows that the scheme is a one-time scheme).

6.13 Suppose Bob is using the Pedersen-van Heyst Fail-Stop Signature Scheme with p = 5087, α = 25 and β = 1866. Suppose the key is

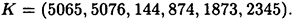
Now, suppose Bob finds the signature (2219, 458) has been forged on the message 4785.

(a) Prove that this forgery satisfies the verification condition, so it is a valid signature.

(b) Show how Bob will compute the proof of forgery, a₀, given this forged signature.

Table of Contents