Appendix E: Optimization

Consider the following simple 2 — 3 payoff matrix in which the elements represent dollar rewards to R.

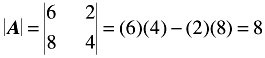
We wish to determine which strategies R and C should choose. Suppose that R chooses R ₁ , which means that he chooses the first row, then he can be certain of winning at least $2 and at most $5. If he chooses R ₂ , he could lose $5 but he might win as much as $6. In view of the wide range of possibilites here, it appears that R should examine more carefully his possible strategies to determine how much he can win even if C is clever or lucky enough to choose his best possible strategy each time.

If R were to choose R ₁ , C would certainly choose C ₂ and thus would limit R to winning $2. If R were to choose R ₂ , C would obviously choose C ₁ and thus would cause R to lose $5. The two elements that represent these two possibilites have been enclosed in circles in the matrix of Figure E.1. They represent the worst that can happen to R regardless of how clever C may be in anticipating which strategy R will select. If R wishes to protect himself as best possible against these undesirable possibilities, he should choose R ₁ . Choosing R ₁ makes it certain that R will win at least $2, and possibly more if it should happen that C does not select his best strategy. Although neither opponent knows which strategy the other will choose, one of them may outguess the other and may gain considerably thereby. The preceding analysis guards R against the occurrence of this possibility.

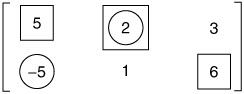
Figure E.1: Strategies for R and C.

Now consider which strategy C should employ . He wishes to keep the amount to be won by R as small as possible because he is required to pay R when R wins. If he reasons in the same manner as R does, he will examine each of his possible strategies to see how well he can do even if R is clever enough to anticipate which strategy C will select. Thus, if C were to select C ₁ , R would choose R ₁ and win $5.

If C were to select C ₂ , R would choose R ₁ and win $2. If C were to select C ₃ , R would choose R ₂ and win $6. Each of the elements representing these three possibilities has been enclosed in a square in Figure E.1. They represent the worst that can happen to C regardless of how clever or lucky R may be. If C wishes to protect himself as best possible against these undesirable possibilities, he should choose C ₂ because that minimizes the amount that he will need to pay to R.

The preceding analysis, which assumes that R wishes to maximize his winnings and C wishes to minimize his losses, leads to the conclusion that R should choose strategy R ₁ and C should choose strategy C ₂ . If the game is played with these two strategies, R will win $2 from C. The number 2 is called the value of this game. It represents the amount that R expects to win and C expects to pay if R and C play their best defensive strategies.

If the best strategies for R and C do not yield a common circle-square element of the payoff matrix, the game does not have a solution, and therefore does not have a value.