C CHART

The c chart is a control chart for the number of nonconformities (defects or concerns) per inspection unit. The c chart is especially easy to make because the number of defects is plotted directly on the control chart. This control chart should be used when the following conditions exist:

• More than one defect is possible for a single part (e.g., missing bushing, an incomplete invoice, an incomplete order, and so on).

• Defects occur evenly throughout the process stream (e.g., flows per coil of wire, bubbles per windshield , typographical errors per report, and so on).

STEPS FOR CONSTRUCTING A C CHART

1. Establish a Sampling Plan for the Control Chart

1. Determine an appropriate sample size (n). The sample size used to construct a c chart must be constant. The sample size must also be large enough so that a typical sample subgroup contains nonconformities (defects).

2. Determine a sampling frequency. Collect sample subgroups often enough to provide diagnostic information. People must identify special causes of variation and search for the cause of the unexpected variation. Problem-solving activities are easier to perform when the subgroups are collected at reasonable intervals. The rate of process change defines an appropriate sampling interval. A very frequent sampling plan is needed for a process that changes often. Stable processes can tolerate less frequent sampling plans. When insufficient information is available for planning a sampling frequency, sample as often as possible. After a stable and in-control process is established, the time interval between sample subgroups may be increased slowly.

3. Record the process data on the control chart. Record the number of defects or concerns (c), sample size ( n ), time, shift, and date for each subgroup on an attribute control chart form. Maintain a process log as a record of all major changes to the process (e.g., changes in machinery, material, methods , or personnel). This log helps people identify the causes of out-of-control conditions.

2. Calculate the Process Center Line

Calculate the mean number of nonconformities (cbar) after collecting 25 subgroups. Use the following formula:

cbar = & pound ; c · k = ( c ₁ + c ₂ + · · · + c _k ) · k

where

c bar	=	mean number of defects
c	=	sum of the defects
k	=	number of inspection units (samples)

3. Calculate the Standard Deviation ( ƒ _c ) for the Number of Defects

The standard deviation for the number of defects is calculated as

where

ƒ c	=	standard deviation for number of defects
cbar	=	mean number of defects

Figure 9.9 shows the sequence of operations needed to calculate the standard deviation for the number of defects with the Sharp series of calculators .

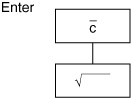
Figure 9.9: The sequence of operations needed to calculate the standard deviation for defects.

4. Calculate Control Limits (UCL and LCL)

The upper control limit (UCL) and the lower control limit (LCL) are boundaries of common variation. They are calculated as three standard deviations above and below the process center line.

UCL c	=	cbar + 3 ƒ c
LCL c	=	cbar - 3 ƒ c

where

UCL	=	upper control limit
LCL	=	lower control limit
cbar	=	process center line (mean number of defects)
ƒ c	=	standard deviation for number of defects

A negative control limit may be calculated for the LCL when the mean number of defects (cbar) is low. Under these conditions, the lower control limit does not exist. Finding no defects is expected for this sampling plan.

5. Determine the Vertical Scale for the C Chart

Determine the vertical scale for control charts only after calculating the process center lines and the control limits. If the scale is determined before these calculations, the process center line may be far from its expected position (the center of the chart). In addition, the control limits may be located beyond the range of the chart's scale. The vertical increments should be selected so that the plotting of the sample points is relatively simple and easily understood . The cbar value should be located about one third to one half of the distance up the vertical scale of the c chart. The UCLc should be positioned approximately two thirds to three quarters of the distance up the scale.

6. Plot the Proportions on the Control Chart

Plot the c values for each sample on the chart. Place each plotted point directly above the data and time-sequence information included in the data table. The plotted points may be connected with a solid line as an aid to the analysis of patterns and trends in the data. Proofread the plotted points and compare them with the calculated proportions before analyzing the control chart.

7. Draw the Process Center Line and Control Limits on the Chart

The cbar line should be drawn as a solid horizontal line. Control limits are usually drawn as a dashed, bold, horizontal line. Date and label all lines. During the initial study phase, the lines are considered trial center line and control limits. These may require revision as the process is modified and improved.

8. Analyze the C Chart for Process Control

Use the five criteria for process control to evaluate the c chart. Identify and note all out-of-control conditions and factors that contribute to instability. In the process log, note the time, shift, date, material lot number, material vendor process parameters, and production personnel included in the process operation during the out-of-control period. The problem-solving techniques included in Chapter 2 will help the identification of special causes of variation.

• Are there any points beyond the control limits?

• Are there runs of seven (7) or more points?

• Are there trends of seven (7) or more points?

• Are there cycles of points?

• Is there unusual variation (use the 1/3 or 2/3 rule)?

If all of the plotted data on the c chart are within the control limits and randomly distributed around the center line, the defective rate for the process is stable and predictable (see Figure 9.10). The process is in control. Unless the process is in control, ongoing control limits cannot be calculated, process capability cannot be studied, and experimental studies cannot be generalized to longer and larger production runs.

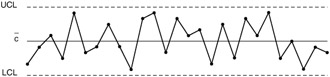
Figure 9.10: A typical stable and predictable process.

If any of the plotted proportions (cbar) are outside of the control limits (see Figure 9.11), this indicates one or more of the following:

• The control limits have been miscalculated or have been drawn incorrectly.

• The plotted proportion beyond the control limit has been miscalculated or plotted improperly.

• The process defect rate has changed significantly from that of the past, which may be good or bad (and the cause for the process change must be identified and investigated).

• The measurement systems or the definition of a nonconformity has changed.

• The process center line calculated from these data is questionable because the center line is influenced by the extreme variation.

Figure 9.11: A process with points out of control limits.

If there is a run of seven or more proportions (cbar) on one side of the center line (see Figure 9.12), this means one or more of the following:

• The process defect rate has changed (or is still different) from that of the past.

• The measurement system or the definition of a nonconformity has changed.

• The control limits calculated from these data are questionable and may require recalculation.

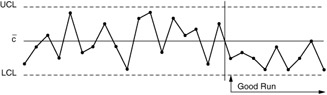
Figure 9.12: A process with a run below the cbar.

A trend (up or down) of seven or more sample values (see Figure 9.13) means that the process defect rate is gradually changing or drifting. The cause of the change must be identified and assessed. Undesirable upward trends must be eliminated from the manufacturing process. Trends due to process improvements (downward trends) must be continued . The process should be made stable and predictable at a new and lower level. The process center line, control limits, and capability analyses must be recalculated after the process is controlled at a new level.

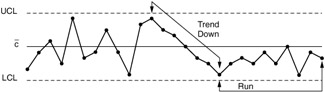
Figure 9.13: A process with a downward trend and a run below the cbar.

Cycles indicate repeating patterns of high and low process defect rates (see Figure 9.14). These are opportunities for improvement because a number of defect rates have been observed . The factors that cause the different levels of the cycle and the optimal condition ( lowest parts of the cycle) must be identified. The defective rate resulting from the optimal conditions must be made the regular level for the process.

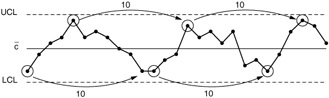
Figure 9.14: A process with cycles.

Unusual variation (see Figure 9.15) in the process defect rate means one or more of the following:

Figure 9.15: A process with unusual variation.

• The control limits have been miscalculated.

• The center line for the control chart has been miscalculated.

• The process or sampling plan is stratified.

• The data have been edited or changed from the original readings (excessive rounding errors).

9. Identify and Eliminate the Special Causes of Variation

How people react to control chart signals is the most critical part of the SPC program. To identify and eliminate special variation, people must analyze the process operations and the resources used. In addition to the control chart, fishbone diagrams, Pareto charts, process flow charts, and controlled experiments may be needed to identify and resolve factors that create instability in the process. It is very important to react promptly to eliminate and prevent special causes of variation. A production department's reaction to out-of-control conditions indicates its commitment to understanding and controlling the manufacturing process. The control chart provides signals to help production departments maintain good quality.

10. Extend the Control Limits for Ongoing Process Control

When the data from the operating process (at least 25 subgroups) are consistently within the control limits and in control, the control limits may be extended to future samples of data. Production operators and supervisors should closely monitor the charts and act promptly to correct special causes of variation. If the process is improved, or if extreme sources of variation are eliminated, the process center line and control limits may no longer be appropriate. The changes made to the process may make it necessary to recalculate the process center lines and control limits. When a production department continually improves its operations, control charts require frequent recalculation. The improvement activities are recorded on c charts as downward trends and/or runs below cbar. These out-of-control conditions verify that the process has been improved.