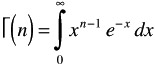GAMMA DISTRIBUTION | Six Sigma and Beyond: Design for Six Sigma, Volume VI

The probability that the nth event (e.g., failure) will occur exactly at the (end) time t, when the events are assumed to occur at a constant rate .

The idea of a constant event rate is the same assumption used for both exponential and Poisson distributions.

The variable time, t, is said to have a gamma distribution.

GAMMA DISTRIBUTION (PDF)

Two parameters:

Scale parameter:	n	(changes scale not shape)
Shape parameter:		(changes shape not scale)
Gamma Function
Mean: ¼ =	Variance: ² =

If 1 < n unimodal shape with mode at: m =
If n 1 non-modal shape with mode at: m = 0

GAMMA FUNCTION

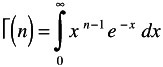
Properties of Gamma Functions

If n = positive integer,

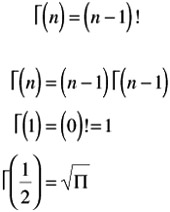
Degrees of freedom (e.g., see chi-square distribution)
If n = v = degrees of freedom (always a positive integer)
If n = even integer:
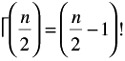
If n = odd integer:

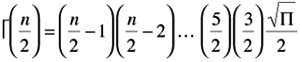
Gamma Distribution and Reliability

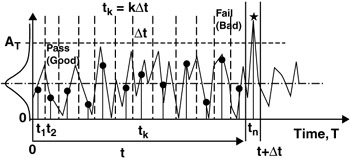
Gamma distribution is used in reliability where a number of partial failures n must occur before a system or item completely fails.

The time to the n-th failure is estimated assuming that the times to individual (partial) failures are exponentially distributed.

Two parameters have the following interpretation:

n is the number of partial failures per complete failure

is the failure rate

Limiting case: When total system failure occurs at the time of the first partial failure n = 1 and the gamma distribution reduces to the exponential distribution.

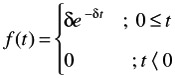
EXAMPLE 1: TIME TO TOTAL SYSTEM FAILURE

To ensure reliability, an important computer system is controlled by a set of four switches. Each switch has a constant failure rate of two per year. The computer system is said to totally fail when there has occurred a total of three switch failures.

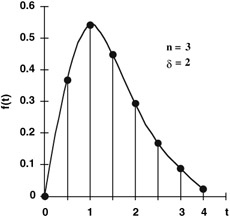
State the parameters and plot the pdf with its mean and mode for the time to total system failure.

Solution: The two parameters are: and n
Failure rate: = 2 failure/year
Number of partial failures to total system failure: n = 3
Mean time to system failure:
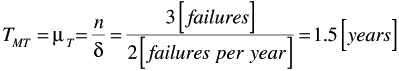
Mode:

Gamma Distribution and Reliability

Probability density function

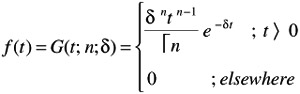
For case of: n = 3 [failures] and = 2 [failure/year]

Gamma function: ˆ (3) = (3 - 1)! = 2! = 2 [f] 1 [f] = 2 [fail] ²

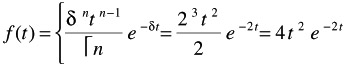
Time ( years ) pdf

t = 0:	f(0)	=	0.0000
t = 0.5	f(.05)	=	0.3679
t = 1.0	f(1.0)	=	0.5416
t = 1.5	f(1.5)	=	0.4481
t = 2.0	f(2.0)	=	0.2931
t = 2.5	f(2.5)	=	0.1685
t = 3.0	f(3.0)	=	0.0892
t = 4.0	f(4.0)	=	0.0215

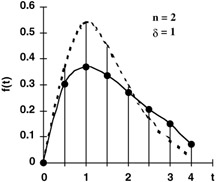
The case when the failure rate is reduced to 1 per year and the total system failure occurs after only two switches fail.

Failure rate: = 1 failure/year

Number of partial failures to total system failure: n = 2

Mean time to system failure:

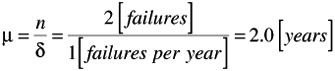
Mode:

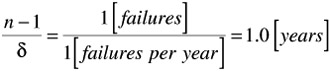
Gamma function: ˆ (2) = (2 - 1)! = 1! = 1 [fail]

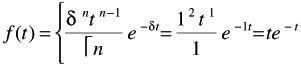
Time (years) pdf

t = 0:	f(0)	=	0.0000
t = 0.5	f(.05)	=	0.3033
t = 1.0	f(1.0)	=	0.3679
t = 1.5	f(1.5)	=	0.3347
t = 2.0	f(2.0)	=	0.2707
t = 2.5	f(2.5)	=	0.2052
t = 3.0	f(3.0)	=	0.1494
t = 4.0	f(4.0)	=	0.0733

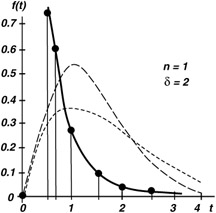
For special case of n = 1; Gamma ’ Exponential Distribution

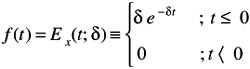
Consider case of: n = 1 [failures] and = 2 [failure/year]

Gamma function: ˆ (1) = (1 - 1)! = 0! = 1 [unitless]

Time (years) pdf

t = 0.2:	f(0)	=	1.3406
t = 0.5	f(.05)	=	0.7358
t = 0.6	f(0.6)	=	0.6024
t = 1.0	f(1.0)	=	0.2707
t = 1.5	f(1.5)	=	0.0996
t = 2.0	f(2.0)	=	0.0366
t = 2.5	f(2.5)	=	0.0135
t = 3.0	f(3.0)	=	0.0050
t = 4.0	f(4.0)	=	0.0007

Reliability Relationships

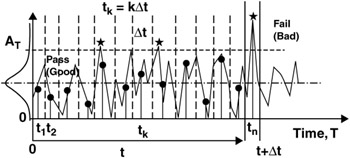
Sample data approach:

n - identical systems are placed in operation at t = 0

g(t) - good; number operating or survive to time t

b(t) - bad; number to fail or survive to time t

where b(t) = n - g(t)

Random variable approach:

T is a continuous random variable representing the time to failure or failure time of a system.

Reliability Function

Sample Space: n = g(t) + b(t)
H Set bad samples:	{b(t) = x}
Set good samples:	{g(t) = n - x}

Reliability is the probability that a system can operate successfully over the time interval from 0 to t. Reliability can also be viewed as the probability that the system will survive beyond a given point in time, t.

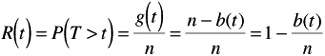
As time increases, chance of failure increases and reliability decreases; as t ’ ˆ or n ’ ˆ , then R(t) ’ 0.

DATA FAILURE DISTRIBUTION

Probability of systems failure as a function of time.

FAILURE RATE OR DENSITY FUNCTION

Failure rate is ratio of the number of failures occurring in time interval At to the size of original population, divided by time interval.

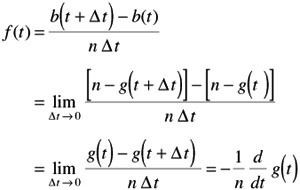
A measure of the overall speed at which failures are occurring

Alternatively, can express the failure rate as the probability that a failure occurs in any given time interval At by taking the time derivative (rate) of the failure distribution Q(t).

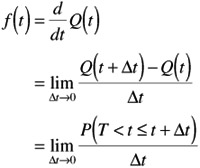
HAZARD RATE FUNCTION

Hazard rate is ratio of the number of failures occurring in time interval ” t to the number of survivors at the beginning of the time interval t, divided by time interval.

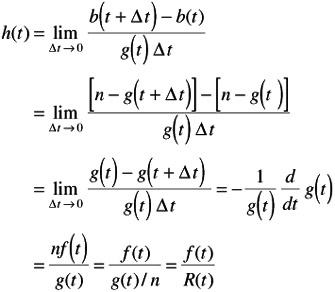
Hazard rate as the conditional probability of failure in the interval (t, t + ” t] given that the system has survived up to the time t:

RELATIONS BETWEEN RELIABILITY AND HAZARD FUNCTIONS

Recall last derivation relating hazard to reliability functions:

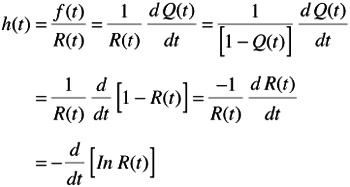
A separable first order differential equation whose solution is:

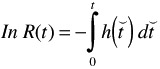
Raising both sides to the power of exponential e:

Reliability function:

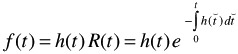
Failure cumulative function:

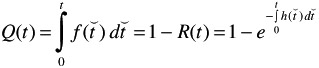
POISSON PROCESS

Probability of exactly x - "failures" occurring in any order within a given time interval (or spatial region):

Time interval
Spatial region (e.g., typos on a page)

Sample Space: n = g + b

H Set bad samples:

{b = x = 5}

Set good samples:

{g = n - x}

Characteristics of Poisson Process

Number of outcomes in a given time interval, n ” t, is independent of the number that occurs in any other interval (no memory).
At most only one single outcome can occur within a small time increment of duration At (or spatial increment ” y).
Probability of an outcome is therefore proportional to the duration of the sample time increments At and is given by

p = ˆ t

Poisson Distribution

The probability distribution of a Poisson random variable, X, representing the number of outcomes occurring in the time interval t is given by

where = average number of outcomes per unit time "mean time between events or failures" and t = n ” t = np mean number of outcomes in time t.

There are two possible ( mutually exclusive) situations for having x - failures in this interval depending upon whether or not a failure occurs in the last ” t increment.

One failure in last increment, then must have

(x - 1) - failures in the interval

1 - failures in the increment

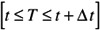
Sample Space: n = g + b

H Set bad samples:

{b = x = 5}

Set good samples:

{g = n - x}
No failure in last increment, then must have

x - failures in the interval

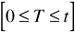
0 - failures in the increment

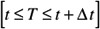
Sample Space: n = g + b

H Set bad samples:

{b = x = 5}

Set good samples:

{g = n - x}

Probability of configuration (1), where one failure occurs in the last increment, is given by:

(x - 1) - failures in the interval or

1 - failures in the increment or

Sample Space: n = g + b

H Set bad samples:	{b = x = 5}
Set good samples:	{g = n - x}

P({b} · {g}) = P({b} {g}) P({g}) = P({b})({g})

where we again assume that the "success" probability of finding one bad sample occurs in increment is a constant

p = ˆ t

Likewise, the average number of "bad" samples in an interval , which is composed of n ” t increments, is

a = np = n ” t =

Probability of configuration (2), where zero failure occurs in the last increment, is given by:

x - failures in the interval or

0 - failures in the increment or

Sample Space: n = g + b

H Set bad samples:	{b = x = 5}
Set good samples:	{g = n - x}

P({b} · {g}) = P({b} {g}) P({g}) = P({b})({g})

where we again assume that the "success" probability of finding no "bad" sample occurs in increment is a constant

p = 1 - q = 1 - ˆ t

As before, the average number of "bad" samples in an interval , which is composed of n ” t increments, is

a = np = n ” t =

The combined probability of these two mutually exclusive configurations of x - failures is given by the sum the probability associated with each configuration:

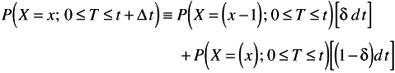
Regrouping like probabilities terms of like kind and dividing by dt

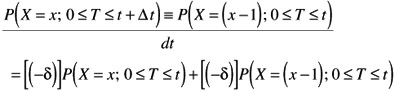
Defining a "Reliability" of having exactly x- failures in a given time interval as the probability:

we can write the non-homogenous differential equation:

where the non-homogenous term depends upon the values of R obtained for all previous values of x. That is, for x = 2, we need to successively find the solutions for R(1;t) and R(0;t)

"Initial Condition" at t = 0 satisfying the certain and impossible outcomes, respectively

yields a Poisson distribution probability density function (a = t):

Example

An average of four (4) private aircraft landings per hour in a small local airport, = 4L/h. What is probability that six (6) aircraft will land in one hour?

The Poisson distribution is

One parameter: a (= np = t)

Mean: ¼ = a

Variance: ² = a

Solution:

Number of aircraft landing in one hour: X = 6L

Average number of landings in one hour: a = 4L

That is, a = t = 4 L/h 1h = 4L

The probability of six aircraft in one hour is then given by

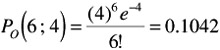
There is a 10.4% chance that six aircraft will land in one hour.