12.5 Performance of Mobile-Mobile Rerouting

12.5 Performance of Mobile-Mobile Rerouting

We now analyze the performance of the mobile-mobile rerouting algorithms. It should be noted for all the subsequent analysis below that for Biswas' scheme, the initial path length between the source and destination base stations is equal to a = b + 2c hops, where b is the length of the fixed path between the source and destination mobile representatives and c is the length to the path between the initial source (resp. destination) base station and the source (resp. destination) mobile representative. In the case of the CBT strategy, the initial path length from the source (resp. destination) base station to the source (resp. initial destination) mobile representative is equal to c hops and the path length between the initial pair of source and destination mobile representative is b hops. Similarly, in the case of Ghai and Singh's scheme, b is the path length between the old (resp. new) source and destination supervisory hosts and c is the length of the path between the initial source (resp. destination) base station and the source (resp. destination) supervisory host. Figures 12.13 through 12.17 are graphical representations of these mobile-mobile rerouting schemes. In these figures, we specify the values of the parameters a, b, and c. For all the metrics that we discuss later, we plot values for rerouting distance for d varying from 1 to 25 for the rerouting schemes. Biswas' scheme, the CBT scheme, Ghai and Singh's worst and best schemes, the IS-41(c) cellular scheme, and Racherla's scheme are represented by the legends Biswas, CBT, Ghai (worst case), Ghai (best case), Cell, and Ours (Racherla), respectively.

Figure 12.13: Ghai and Singh's scheme— (a) worst case; (b) best case.

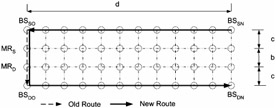
Figure 12.14: Core-based tree scheme.

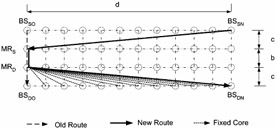
Figure 12.15: IS-41(c) scheme.

Figure 12.16: Racherla's scheme.

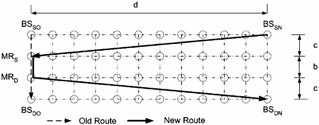
Figure 12.17: Biswas' scheme.

12.5.1 Total Rerouting Distance

Figure 12.18 shows the total rerouting distance as a function of mobile host movement distance (d) for the five rerouting schemes described previously. The figure contains four plots for various values of the initial path length a (a = 3, 27, 39, 63). We make the following observations:

• Racherla's proposed scheme and Ghai's (best case) scheme perform the best because these schemes set up the optimal route. IS-41(c) performs the worst with increasing values of d because of its naive approach of cell forwarding continuously. The rerouting distance for Racherla's scheme and Ghai (best case) is optimal, and for the given topology is a constant and does not vary with increasing values of d. For all the other schemes, the rerouting distance increases with increasing values of d.

• For Biswas' scheme, it can be seen that total rerouting length depends on the length of the initial fixed path. If this initial fixed path b = a (that is, c = 0), then it is the exact same scheme as cell forwarding rerouting. Biswas' strategy is a specialized case of the CBT strategy wherein a core-based tree is replaced by a simple path. It is better to use Biswas' strategy than the CBT strategy in order to reduce the total rerouting distance, if c < b. In case, b > c, it is better to use the CBT strategy.

• For Ghai's (worst case), the CBT and Biswas' scheme, the rerouting distance increases linearly with the increasing values of d. However, the rerouting distance improves when c = d. This is intuitive because when c = d, the new route can be done along the slanted links.

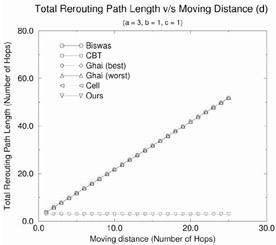
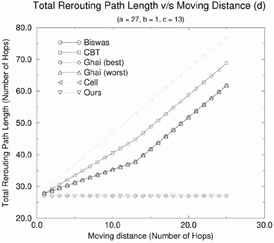
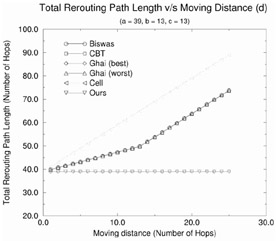
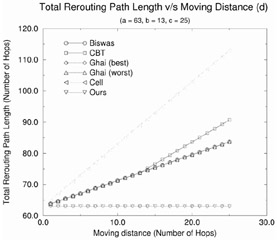
Figure 12.18: Effect of the moving distance on the total rerouting distance for various rerouting schemes.

12.5.2 Cumulative Connection Path Length

Figure 12.19 shows the cumulative connection path length as a function of mobile host movement distance (d) for the rerouting schemes. From the figure, we make the following observations:

• The IS-41(c) scheme does the best because there is no need to remove any of the old paths and every move of the mobile translates to an increase of a unit length increase in the cumulative path.

• Racherla's strategy performs the next best as the cumulative path length is increased by a hops every time the mobile moves. This is because a new optimal path of length a hops needs to be established.

• In case of all the other schemes, the cumulative path length is much higher and grows exponentially. The CCPL for d moves in each of these cases is a sum of all the total rerouting distance values for all moves 1 through d.

• We see again that it is better to use Biswas' strategy than the CBT strategy in order to reduce the cumulative path length, if c < b. In case, b > c, it is better to use the CBT strategy.

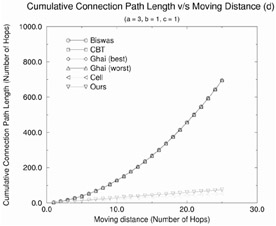
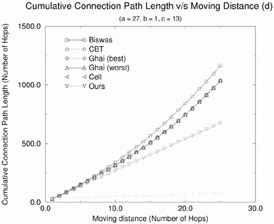
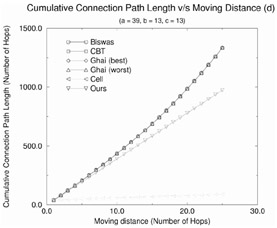
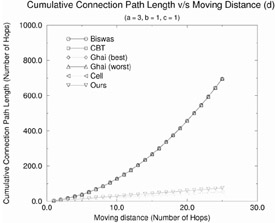
Figure 12.19: Effect of the moving distance on the cumulative connection path length for various rerouting schemes.

12.5.3 Number of Connections

In Figure 12.20, we show the cumulative connection path length as a function of mobile host movement distance (d) for the rerouting schemes. The figure contains two parts showing the plots for various values of the initial path length a (a = 3, 39). From this figure, we observe that the number of connections is minimum and constant (equal to 2) in the case of Racherla's strategy. Biswas' strategy requires also a constant number of connections, namely, 5. Also, the number of connections for the other schemes is dependent on the moving distance.

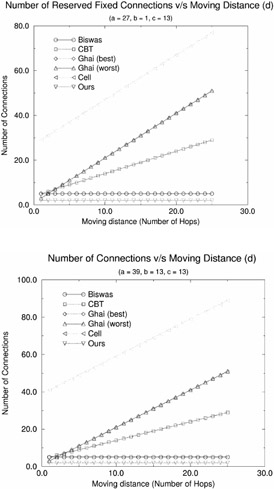
Figure 12.20: Effect of the moving distance on the number of connections established or torn down for various rerouting schemes.

Among the remaining schemes, the CBT scheme requires the least number of connections. Ghai (best case) and Ghai (worst case) and IS-41(c) require the same number of connections. From the observations of the performance of all these rerouting schemes with respect to the metrics, we infer that Racherla's scheme performs the best as far as the total rerouting distance and the number of connections are concerned. Ghai (best case) performs as well as our scheme in terms of the total rerouting distance. However, it requires many more connections to be established and incurs more cumulative cost in establishing connections. Also in the worst case, the routes for Ghai and Singh's scheme are suboptimal. In addition, Ghai and Singh's strategy requires specialized supervisory hosts and a tree-based network for optimal performance. IS-41(c) performs the best with respect to the cumulative cost incurred in establishing connections. However, IS-41(c) requires a high number of connections and its total rerouting distance is very high. CBT is a generalized case of Biswas' scheme. In general, the CBT scheme requires more resources than Biswas' scheme and its performance advantage in terms of total rerouting distance over Biswas' scheme is highly dependent on the underlying topology and the details of the core-based tree.