Projections and Coordinate Systems 1
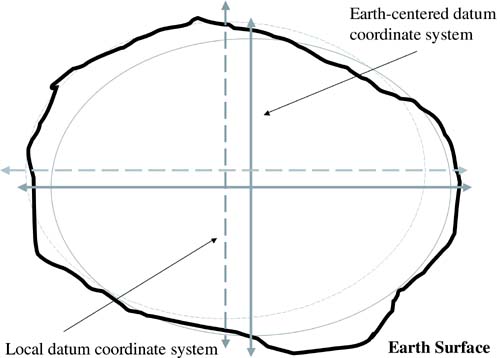
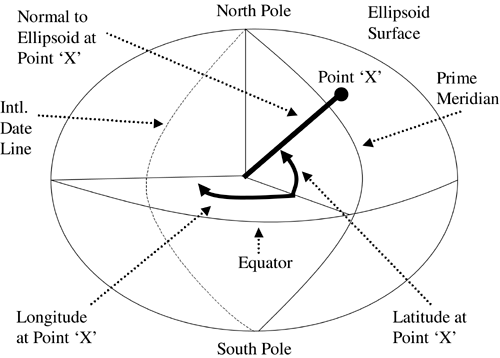
Projections and Coordinate Systems [1]The world is not the flat, paper roadmap you might use to navigate with in your car. The earth is spherical, and there are actually several approaches to approximate the earth's shape and provide a system for identifying a position on the earth's surface. The earth's shape actually resembles an ellipsoid, as it revolves easterly on its axis, creating centrifugal force and causing a flattening at the North and South Poles and a bulge at the equator. The ellipsoid is only a mathematical approximation of the earth, and there are several different models to provide a frame of reference for calculating coordinates on the earth's surface, each designed to closely fit the earth's surface in a particular geographical area. As shown in Figure 4.9, each datum defines the position of the ellipsoid relative to the center of the earth. Figure 4.9. Datums. A point x on the earth's surface has an east “west position (longitude) and a north “south position (latitude), as seen in Figure 4.10. Figure 4.10. Earth as an Ellipsoid. Latitude is defined as the angle formed by the intersection of a line perpendicular to the earth's surface at the point and a plane passing through the equator. North of the equator, points have a positive value. Points south of the equator have a negative value. The value range for latitude is from “90 degrees to 90 degrees. Lines of latitude are also called parallels because lines of latitude run parallel to the equator. Longitude is defined by the angle between the prime meridian and a plane that passes through the point and the North and South Poles. The most common prime meridian is a plane that passes through the North and South Poles and Greenwich, United Kingdom. Longitude values range from 0 degrees at the prime meridian to 180 degrees at the international dateline . West of the prime meridian is negative longitude and east of the prime meridian is positive longitude. To be most useful in software applications (and to make flat maps), it is necessary to get the spherical three-dimensional model into two dimensions. This process is called a projection , and involves a mathematical transformation of a geographical location (longitude and latitude) on a sphere to a corresponding location (x and y) on a flat, two-dimensional surface. The x-axis represents position values from east to west (longitude), and the y-axis represents position values from north to south (latitude). Different projections create different map distortions. [2] Some projections work best for large-scale, detailed maps of a very small area, whereas other projections work best for small-scale maps that need to display large, country- or continent - sized areas. There are four primary types of projection: conformal projections, equal area projections, equidistant projections, and true directions projections. Conformal projections focus on preserving shape, which is done by preserving angles at the expense of size. An equal area projection preserves the area of displayed features by distorting shape, angle, and scale. Equidistant projections maintain the distances from the center of the map, but do not maintain scale. True directions projections maintain the distance between two points on a spherical surface as a straight line on a flat surface. The best coordinate system and projection method depends on the region in which your mobile location services applications are to be deployed. It is valuable to have the flexibility to change projections based on the application and scale you are planning to use. The Universal Transverse Mercator (UTM) is an international metric coordinate with worldwide coverage. UTM is a conical projection and provides coverage between 84 degrees north and 80 degrees south (see Figure 4.11). It has the advantage of being well defined and mathematically consistent for the entire earth, and could be a good choice for applications that require continent-wide or worldwide deployment. [3] Figure 4.11. UTM Conical Projection. |
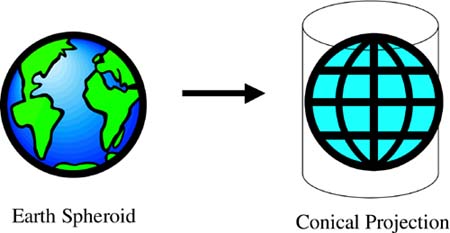
EAN: 2147483647
Pages: 150