Trees

A tree is a way of organizing data. The idea is that each data element, called a node , contains data as well as links to other nodes. Each tree begins with a root node , and the tree builds from there. Generally, we draw trees upside down with the root node on top and the connections from it going down. Nodes at the bottom (furthest from the root) are called leaf nodes. See Figure 10.7 for an example of a tree.

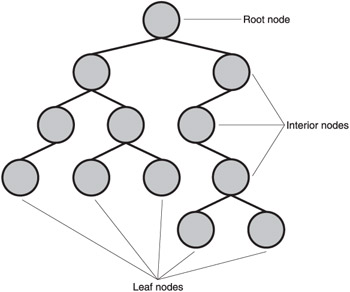
Figure 10.7: A tree structure contains a root node, interior nodes, and leaf nodes.

Tree structures are commonly used data formats in programming. Trees have countless applications, but this chapter focuses on using them to build computer AI. Just be aware that you can use trees to store data for many different kinds of applications.

Now we need to define what a node is. Each node, as I've said, has links to other nodes further down the tree. The nodes further down the tree are called child nodes . Nodes further up the tree are called parent nodes .

Tip  

One particular type of tree, called a binary tree , contains nodes with a maximum of two children. These kinds of trees can store ordered data ”that is, data that has been sorted into a particular order. By storing sorted data in a tree structure, you can increase performance when accessing, adding, and deleting data (nodes). This performance increase is most pronounced when there are many nodes. With few nodes, the additional work required to iterate the tree (recursion) is more work than the tree structure provides in benefit.

Using a tree structure requires recursion because a simple loop cannot handle this situation. If you are modeling data with a tree structure, you want to define methods to add data, remove data, and access data into the tree structure. All these methods are recursive.

Our use of the tree structure is limited to what we need to build a game tree.