11.9 Sums

< Free Open Study >

Many programs need to deal with heterogeneous collections of values. For example, a node in a binary tree can be either a leaf or an interior node with two children; similarly, a list cell can be either nil or a cons cell carrying a head and a tail,^[6] a node of an abstract syntax tree in a compiler can represent a variable, an abstraction, an application, etc. The type-theoretic mechanism that supports this kind of programming is variant types.

Before introducing variants in full generality (in §11.10), let us consider the simpler case of binary sum types. A sum type describes a set of values drawn from exactly two given types. For example, suppose we are using the types

   PhysicalAddr = {firstlast:String, addr:String};   VirtualAddr  = {name:String, email:String};

to represent different sorts of address-book records. If we want to manipulate both sorts of records uniformly (e.g., if we want to make a list containing records of both kinds), we can introduce the sum type^[7]

   Addr = PhysicalAddr + VirtualAddr;

each of whose elements is either a PhysicalAddr or a VirtualAddr.

We create elements of this type by tagging elements of the component types PhysicalAddr and VirtualAddr. For example, if pa is a PhysicalAddr, then inl pa is an Addr. (The names of the tags inl and inr arise from thinking of them as functions

   inl : PhysicalAddr → PhysicalAddr+VirtualAddr   inr : VirtualAddr → PhysicalAddr+VirtualAddr

that "inject" elements of PhysicalAddr or VirtualAddr into the left and right components of the sum type Addr. Note, though, that they are not treated as functions in our presentation.)

In general, the elements of a type T₁+T₂ consist of the elements of T₁, tagged with the token inl, plus the elements of T₂, tagged with inr.

To use elements of sum types, we introduce a case construct that allows us to distinguish whether a given value comes from the left or right branch of a sum. For example, we can extract a name from an Addr like this:

   getName = λa:Addr.     case a of       inl x ⇒ x.firstlast     | inr y ⇒ y.name;

When the parameter a is a PhysicalAddr tagged with inl, the case expression will take the first branch, binding the variable x to the PhysicalAddr; the body of the first branch then extracts the firstlast field from x and returns it. Similarly, if a is a VirtualAddr value tagged with inr, the second branch will be chosen and the name field of the VirtualAddr returned. Thus, the type of the whole getName function is Addr→String.

The foregoing intuitions are formalized in Figure 11-9. To the syntax of terms, we add the left and right injections and the case construct; to types, we add the sum constructor. For evaluation, we add two "beta-reduction" rules for the case construct-one for the case where its first subterm has been reduced to a value v₀ tagged with inl, the other for a value v₀ tagged with inr; in each case, we select the appropriate body and substitute v₀ for the bound variable. The other evaluation rules perform evaluation in the first subterm of case and under the inl and inr tags.

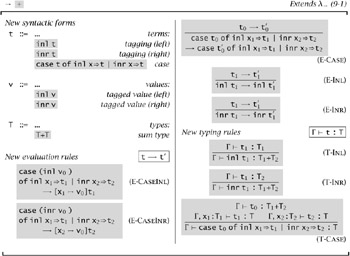
Figure 11-9: Sums

The typing rules for tagging are straightforward: to show that inl t₁ has a sum type T₁+T₂, it suffices to show that t₁ belongs to the left summand, T₁, and similarly for inr. For the case construct, we first check that the first subterm has a sum type T₁+T₂, then check that the bodies t₁ and t₂ of the two branches have the same result type T, assuming that their bound variables x₁ and x₂ have types T₁ and T₂, respectively; the result of the whole case is then T. Following our conventions from previous definitions, Figure 11-9 does not state explicitly that the scopes of the variables x₁ and x₂ are the bodies t₁ and t₂ of the branches, but this fact can be read off from the way the contexts are extended in the typing rule T-CASE.

11.9.1 Exercise [⋆⋆]

Note the similarity between the typing rule for case and the rule for if in Figure 8-1: if can be regarded as a sort of degenerate form of case where no information is passed to the branches. Formalize this intuition by defining true, false, and if as derived forms using sums and Unit.

Sums and Uniqueness of Types

Most of the properties of the typing relation of pure λ_→ (cf. §9.3) extend to the system with sums, but one important one fails: the Uniqueness of Types theorem (9.3.3). The difficulty arises from the tagging constructs inl and inr. The typing rule T-INL, for example, says that, once we have shown that t₁ is an element of T₁, we can derive that inl t₁ is an element of T₁+T₂for any type T₂. For example, we can derive both inl 5 : Nat+Nat and inl 5 : Nat+Bool (and infinitely many other types). The failure of uniqueness of types means that we cannot build a typechecking algorithm simply by "reading the rules from bottom to top," as we have done for all the features we have seen so far. At this point, we have various options:

We can complicate the typechecking algorithm so that it somehow "guesses" a value for T₂. Concretely, we hold T₂ indeterminate at this point and try to discover later what its value should have been. Such techniques will be explored in detail when we consider type reconstruction (Chapter 22).
We can refine the language of types to allow all possible values for T₂ to somehow be represented uniformly. This option will be explored when we discuss subtyping (Chapter 15).
We can demand that the programmer provide an explicit annotation to indicate which type T₂ is intended. This alternative is the simplest-and it is not actually as impractical as it might at first appear, since, in full-scale language designs, these explicit annotations can often be "piggybacked" on other language constructs and so made essentially invisible (we'll come back to this point in the following section). We take this option for now.

Figure 11-10 shows the needed extensions, relative to Figure 11-9. Instead of writing just inl t or inr t, we write inl t as T or inr t as T, where T specifies the whole sum type to which we want the injected element to belong. The typing rules T-INL and T-INR use the declared sum type as the type of the injection, after checking that the injected term really belongs to the appropriate branch of the sum. (To avoid writing T₁+T₂ repeatedly in the rules, the syntax rules allow any type T to appear as an annotation on an injection. The typing rules ensure that the annotation will always be a sum type, if the injection is well typed.) The syntax for type annotations is meant to suggest the ascription construct from §11.4: in effect these annotations can be viewed as syntactically required ascriptions.

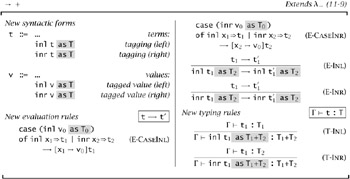
Figure 11-10: Sums (With Unique Typing)

^[6]These examples, like most real-world uses of variant types, also involve recursive types-the tail of a list is itself a list, etc. We will return to recursive types in Chapter 20.

^[7]The fullsimple implementation does not actually support the constructs for binary sums that we are describing here-just the more general case of variants described below.

< Free Open Study >