Cryptography: Theory and Practice:Identification Schemes | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

There remains to be considered the possibility that (a₁, a₂) = (b₁, b₂). If this happens, then the value of c cannot be computed as described above. However, we will argue that (a₁, a₂) = (b₁, b₂) will happen only with very small probability 1/q, so the procedure whereby Alice and Olga compute c will almost surely succeed.

Define

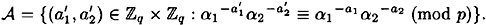
That is, 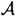consists of all the possible ordered pairs that could be Alice’s secret exponents. Observe that

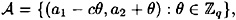
where 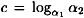. Thus 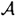consist of q ordered pairs.

The ordered pair (b₁, b₂) computed by Olga is certainly in the set 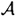. We will argue that the value of the pair (b₁, b₂) is independent of the value of the pair (a₁, a₂) that comprises Alice’s secret exponents. Since (a₁, a₂) was originally chosen at random by Alice, it must be the case that the probability that (a₁, a₂) = (b₁, b₂) is 1/q.

So, we need to say what we mean by (b₁, b₂) being “independent” of (a₁, a₂). The idea is that Alice’s pair (a₁, a₂) is one of the q possible ordered pairs in the set 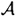, and no information about which is the “correct” ordered pair is revealed by Alice identifying herself to Olga. (Stated informally, Olga knows that an ordered pair from 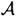comprises Alice’s exponents, but she has no way of telling which one.)

Let’s look at the information that is exchanged during the identification protocol. Basically, in each execution of the protocol, Alice chooses a γ; Olga chooses an r; and Alice reveals y₁ and y₂ such that

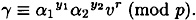
Recall that Alice computes

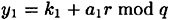
and

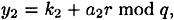
where

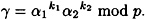
But note that k₁ and k₂ are not revealed (nor are a₁ and a₂).

The particular quadruple (γ, r, y₁, y₂) that is generated during one execution of the protocol appears to depend on Alice’s ordered pair (a₁, a₂), since y₁ and y₂ are defined in terms of a₁ and a₂. But we will show that each such quadruple could equally well be generated from any other ordered pair 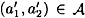. To see this, suppose 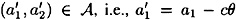and 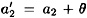where 0 ≤ θ ≤ q - 1. We can express y₁ and y₂ as follows:

and

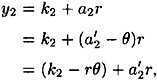
where all arithmetic is performed in 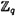. That is, the quadruple (γ,r,y₁,y₂) is also consistent with the ordered pair 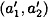using the random choices 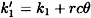and 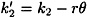to produce (the same) γ. We have already noted that the values of k₁ and k₂ are not revealed by Alice, so the quadruple (γ,r,y₁,y₂) yields no information regarding which ordered pair in 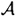Alice is actually using for her secret exponents. This completes the proof.

This security proof is certainly quite elegant and subtle. It would perhaps be useful to recap the features of the protocol that lead to the proof of security. The basic idea involves having Alice choose two secret exponents rather than one. There are a total of q pairs in the set 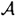that are “equivalent” to Alice’s pair (a₁, a₂). The fact that leads to the ultimate contradiction is that knowledge of two different pairs in 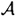provides an efficient method of computing the discrete logarithm c. Alice, of course, knows one pair in 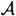; and we proved that if Olga can impersonate Alice, then Olga is able to compute a pair in 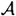which (with high probability) is different from Alice’s pair. Thus Alice and Olga together can find two pairs in 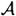and compute c, which provides the desired contradiction.

Here is an example to illustrate the computation of 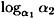by Alice and Olga.

Example 9.5

As in Example 9.4, we will take p = 88667, q = 1031 and t = 10, and assume that v = 13078.

Suppose Olga has determined that

Then she can compute

b₁ = (131 - 890)(489 - 199)^-1 mod 1031 = 456

and

b₂ = (287 - 303)(489 - 199)^-1 mod 1031 = 519.

Now, using the values of a₁ and a₂ supplied by Alice, the value

c = (846 - 456)(519 - 515)^-1 mod 1031 = 613

is computed. This value c is in fact 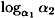as can be verified by calculating

58902⁶¹³ mod 88667 = 73611.

Finally, we should emphasize that, although there is no known proof that the Schnorr Scheme is secure (even assuming that the discrete logarithm problem is intractible), neither is there any known weakness in the scheme. Actually, the Schnorr Scheme might be preferred in practice to the Okamoto Scheme simply because it is somewhat faster.

Table of Contents