Cryptography: Theory and Practice:Identification Schemes | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

9.4 The Guillou-Quisquater Identification Scheme

In this section, we describe another identification scheme, due to Guillou and Quisquater, that is based on RSA.

The set-up of the scheme is as follows: The TA chooses two primes p and q and forms the product n = pq. The values of p and q are secret, while n is public. As is usually the case, p and q should be chosen large enough that factoring n is intractible. Also, the TA chooses a large prime integer b which will function as a security parameter as well as being a public RSA encryption exponent; to be specific, let us suppose that b is a 40-bit prime. Finally, the TA chooses a signature scheme and hash function.

The certificate issued to Alice by the TA is constructed as described in Figure 9.6. When Alice wants to prove her identity to Bob, say, the protocol of Figure 9.7 is executed. We will prove that the Guillou-Quisquater Scheme is sound and complete. However, the scheme has not been proved to be secure (even assuming that the RSA cryptosystem is secure).

Figure 9.6 Issuing a certificate to Alice

Figure 9.7 The Guillou-Quisquater identification scheme

Example 9.6

Suppose the TA chooses p = 467 and q = 479, so n = 223693. Suppose also that b = 503 and Alice’s secret integer u = 101576. Then she will compute

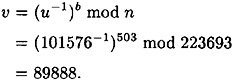
Now, let’s assume that Alice is proving her identity to Bob and she chooses k = 187485; then she gives Bob the value

Suppose Bob responds with the challenge r = 375. Then Alice will compute

and gives it to Bob. Bob then verifies that

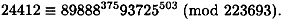
Hence, Bob accepts Alice’s proof of identity.

As is generally the case, proving completeness is quite simple:

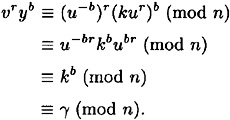
Now, let us consider soundness. We will prove that the scheme is sound provided that it is infeasible to compute u from v. Since v is formed from u by RSA encryption, this is a plausible assumption to make.

THEOREM 9.4

Suppose Olga knows a value γ for which she has probability ∈ > 1/b of successfully impersonating Alice in the verification protocol. Then, in polynomial time, Olga can compute u.

PROOF For some γ, Olga can compute values y₁, y₂, r₁, r₂ with r₁ ≠ r₂, such that

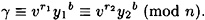
Suppose, without loss of generality, that r₁ > r₂. Then we have

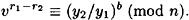
Since 0 < r₁ - r₂ < b and b is prime, t = (r₁ - r₂)^-1 mod b exists, and it can be computed in polynomial time by Olga using the Euclidean algorithm. Hence, we have that

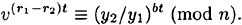
Now,

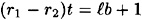
for some positive integer 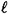, so

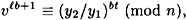
or equivalently,

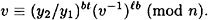
Now raise both sides of the congruence to the power b^-1 mod φ(n), to get the following:

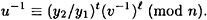
Finally, compute the inverse modulo n, of both sides of this congruence, to obtain the following formula for u:

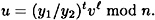
Olga can use this formula to compute u in polynomial time.

Example 9.7

As in the previous example, suppose that n = 223693, b = 503, u = 101576 and v = 89888. Suppose Olga has learned that

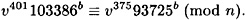
She will first compute

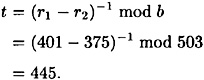
Figure 9.8 Issuing a value u to Alice

Next, she calculates

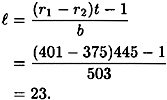
Finally, she can obtain the secret value u as follows:

Thus Alice’s secret exponent has been compromised.

9.4.1 Identity-based Identification Schemes

The Guillou-Quisquater Identification Scheme can be transformed into what is known as an identity-based identification scheme. This basically means that certificates are not necessary. Instead, the TA computes the value of u as a function of Alice’s ID string, using a public hash function h with range 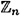. This is done as indicated in Figure 9.8. The identification protocol now works as described in Figure 9.9. The value v is computed from Alice’s ID string via the public hash function h. In order to carry out the identification protocol, Alice needs to know the value of u, which can be computed only by the TA (assuming that the RSA cryptosystem is secure). If Olga tries to identify herself as Alice, she will not succeed because she does not know the value of u.

Figure 9.9 The Guillou-Quisquater identity-based identification scheme

9.5 Converting Identification to Signature Schemes

There is a standard method of converting an identification scheme to a signature scheme. The basic idea is to replace the verifier (Bob) by a public hash function, h. In a signature scheme obtained by this approach, the message is not hashed before it is signed; the hashing is integrated into the signing algorithm.

We illustrate this approach by converting the Schnorr Scheme into a signature scheme. See Figure 9.10. In practice, one would probably take the hash function h to be the SHS, with the result reduced modulo q. Since the SHS produces a bitstring of length 160 and q is a 160-bit prime, the modulo q reduction is necessary only if the message digest produced by the SHS exceeds q; and even in this situation it is necessary only to subtract q from the result.

In proceeding from an identification scheme to a signature scheme, we replaced a 40-bit challenge by a 160-bit message digest. 40 bits suffice for a challenge since an impostor needs to be able to guess the challenge in order to precompute a response that will be accepted. But in the context of a signature scheme, we need message digests of a much larger size, in order to prevent attacking the scheme by finding collisions in the hash function.

Other identification schemes can be converted to signature schemes in a similar fashion.

Figure 9.10 Schnorr Signature Scheme

Table of Contents