Cryptography: Theory and Practice:Signature Schemes
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
We now turn to the disavowal protocol. This protocol consists of two runs of the verification protocol and is presented in Figure 6.8.
Steps 1-4 and steps 5-8 comprise two unsuccessful runs of the verification protocol. Step 9 is a “consistency check” that enables Alice to determine if Bob is forming his responses in the manner specified by the protocol.
The following example illustrates the disavowal protocol.
Example 6.6
As before, suppose p = 467, α = 4, a = 101 and β = 449. Suppose the message x = 286 is signed with the (bogus) signature y = 83, and Bob wants to convince Alice that the signature is invalid.

Figure 6.8 Disavowal protocol
Suppose Alice begins by choosing the random values e1 = 45, e2 = 237. Alice computes c = 305 and Bob responds with d = 109. Then Alice computes
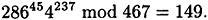
Since 149 ≠ 109, Alice proceeds to step 5 of the protocol.
Now suppose Alice chooses the random values f1 = 125, f2 = 9. Alice computes C = 270 and Bob responds with D = 68. Alice computes
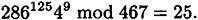
Since 25 ≠ 68, Alice proceeds to step 9 of the protocol and performs the consistency check. This check succeeds, since
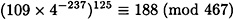
and
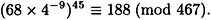
Hence, Alice is convinced that the signature is invalid.
We have to prove two things at this point:
- 1. Bob can convince Alice that an invalid signature is a forgery.
- 2. Bob cannot make Alice believe that a valid signature is a forgery except with a very small probability.
THEOREM 6.2
If 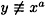 (mod p), and Alice and Bob follow the disavowal protocol, then
(mod p), and Alice and Bob follow the disavowal protocol, then
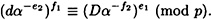
PROOF Using the facts that
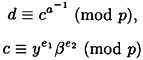
and
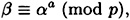
we have that
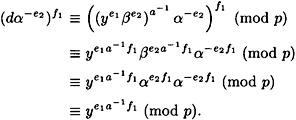
A similar computation, using the facts that 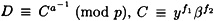 (mod p) and β ≡ αa (mod p), establishes that
(mod p) and β ≡ αa (mod p), establishes that
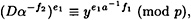
so the consistency check in step 9 succeeds.
Now we look at the possibility that Bob might attempt to disavow a valid signature. In this situation, we do not assume that Bob follows the protocol. That is, Bob might not construct d and D as specified by the protocol. Hence, in the following theorem, we assume only that Bob is able to produce values d and D which satisfy the conditions in steps 4, 8, and 9 of the protocol presented in Figure 6.8.
THEOREM 6.3
Suppose y ≡ xa (mod p) and Alice follows the disavowal protocol. If
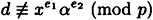
and
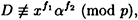
then the probability that
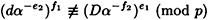
is 1 - 1/q.
PROOF Suppose that the following congruences are satisfied:
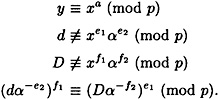
We will derive a contradiction.
The consistency check (step 9) can be rewritten in the following form:
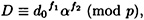
where
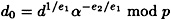
is a value that depends only on steps 1-4 of the protocol.
Applying Theorem 6.1, we conclude that y is a valid signature for d0 with probability 1 - 1/q. But we are assuming that y is a valid signature for x. That is, with high probability we have
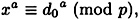
which implies that x = d0.
However, the fact that
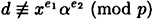
means that
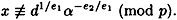
Since
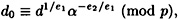
we conclude that x ≠ d0 and we have a contradiction.
Hence, Bob can fool Alice in this way with probability 1/q.
6.6 Fail-stop Signatures
A fail-stop signature scheme provides enhanced security against the possibility that a very powerful adversary might be able to forge a signature. In the event that Oscar is able to forge Bob’s signature on a message, Bob will (with high probability) subsequently be able to prove that Oscar’s signature is a forgery.
In this section, we describe a fail-stop signature scheme constructed by van Heyst and Pedersen in 1992. This is a one-time scheme (only one message can be signed with a given key). The system consists of signing and verification algorithms, as well as a “proof of forgery” algorithm. The description of the signing and verification algorithms of the van Heyst and Pedersen Fail-stop Signature Scheme is presented in Figure 6.9.
It is straightforward to see that a signature produced by Bob will satisfy the verification condition, so let’s turn to the security aspects of this scheme and how the fail-stop property works. First we establish some important facts relating to the keys of the scheme. We begin with a definition. Two keys (γ1, γ2, a1, a2, b1, b2) and 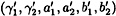 are said to be equivalent if
are said to be equivalent if 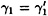 and
and 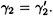 . It is easy to see that there are exactly q2 keys in any equivalence class.
. It is easy to see that there are exactly q2 keys in any equivalence class.
We establish several lemmas.
LEMMA 6.4
Suppose K and K′ are equivalent keys and suppose that verK (x, y) = true. Then verK′ (x, y) = true.
PROOF Suppose K = (γ1, γ2, a1, a2, b1, b2) and K′ = (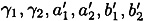 ), where
), where
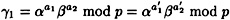
and
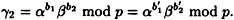
Suppose x is signed using K, producing the signature y = (y1, y2), where
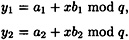
Now suppose that we verify y using K′:
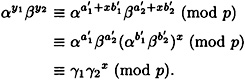
Thus, y will also be verified using K′.

Figure 6.9 van Heyst and Pedersen Fail-stop Signature Scheme
LEMMA 6.5
Suppose K is a key and y = sigK(x). Then there are exactly q keys K′ equivalent to K such that y = sigK′ (x).
PROOF Suppose γ1 and γ2 are the public components of K. We want to determine the number of 4-tuples (a1, a2, b1, b2) such that the following congruences are satisfied:
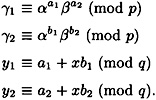
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133