Cryptography: Theory and Practice:Signature Schemes
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
Since α generates G, there exist unique exponents 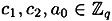 such that
such that
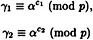
and
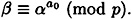
Hence, it is necessary and sufficient that the following system of congruences be satisfied:
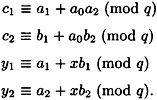
This system can, in turn, be written as a matrix equation in 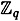 , as follows:
, as follows:
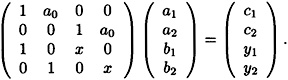
Now, the coefficient matrix of this system can be seen to have rank 1 three: Clearly, the rank is at least three since rows 1, 2 and 4 are linearly independent over 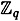 . And the rank is at most three since
. And the rank is at most three since
1the rank of a matrix is the maximum number of linearly independent rows it contains
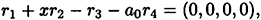
where ri denotes ith row of the matrix.
Now, this system of equations has at least one solution, obtained by using the key K. Since the rank of the coefficient matrix is three, it follows that the dimension of the solution space is 4 - 3 = 1, and there are exactly q solutions. The result follows.
By similar reasoning, the following result can be proved. We omit the proof.
LEMMA 6.6
Suppose K is a key, y = sigK(x), and verK (x′, y′) = true, where x′ ≠ x. Then there is at most one key K′ equivalent to K such that y = sigK′(x) and y′ = sigK′(x′).
Let’s interpret what the preceding two lemmas say about the security of the scheme. Given that y is a valid signature for message x, there are q possible keys that would have signed x with y. But for any message x′ ≠ x, these q keys will produce q different signatures on x′. Thus, the following theorem results.
THEOREM 6.7
Given that sigK(x) = y and x′ ≠ x, Oscar can compute sigK(x′) with probablity 1/q.
Note that this theorem does not depend on the computational power of Oscar: the stated level of security is obtained because Oscar cannot tell which of q possible keys is being used by Bob. So the security is unconditional.
We now go on to look at the fail-stop concept. What we have said so far is that, given a signature y on message x, Oscar cannot compute Bob’s signature y′ on a different message x′. It is still conceivable that Oscar can compute a forged signature y″ ≠ sigK(x′) which will still be verified. However, if Bob is given a valid forged signature, then with probability 1 - 1/q he can produce a “proof of forgery.” The proof of forgery is the value a0 = logα β, which is known only to the central authority.
So we assume that Bob possesses a pair (x′, y″) such that verK(x′, y″) = true and y″ ≠ sigK(x′). That is,
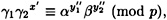
where y″ = (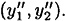 ). Now, Bob can compute his own signature on x′, namely y′ = (
). Now, Bob can compute his own signature on x′, namely y′ = (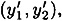 ), and it will be the case that
), and it will be the case that
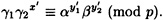
Hence,
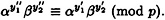
Writing 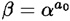 mod p, we have that
mod p, we have that
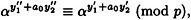
or
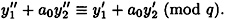
This simplifies to give
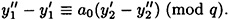
Now, 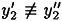 (mod q) since y′ is a forgery. Hence, (
(mod q) since y′ is a forgery. Hence, (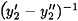 )-1 mod q exists, and
)-1 mod q exists, and
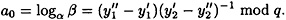
Of course, by accepting such a proof of forgery, we assume that Bob cannot compute the discrete logarithm logα β by himself. This is a computational assumption.
Finally, we remark that the scheme is a one-time scheme since Bob’s key K can easily be computed if two messages are signed using K.
We close with an example illustrating how Bob can produce a proof of forgery.
Example 6.7
Suppose p = 3467 = 2 × 1733 + 1. The element α = 4 has order 1733 in 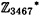 . Suppose that a0 = 1567, so
. Suppose that a0 = 1567, so
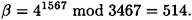
(Recall that Bob knows the values of α and β, but not a0.) Suppose Bob forms his key using a1 = 888, a2 = 1024, b1 = 786 and b2 = 999, so
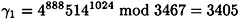
and
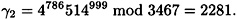
Now, suppose Bob is presented with the forged signature (822, 55) on the message 3383. This is a valid signature since the verification condition is satisfied:
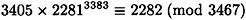
and
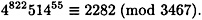
On the other hand, this is not the signature Bob would have constructed. Bob can compute his own signature to be
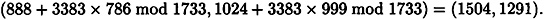
Then, he proceeds to calculate the secret discrete log
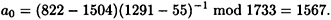
This is the proof of forgery.
6.7 Notes and References
For a nice survey of signature schemes, we recommend Mitchell, Piper, and Wild [MPW92]. This paper also contains the two methods of forging ElGamal signatures that we presented in Section 6.2.
The ElGamal Signature Scheme was presented in ElGamal [EL85]. The Digital Signature Standard was first published by NIST in August 1991, and it was adopted as a standard in December 1994 [NBS94]. There is a lengthy discussion of DSS and the controversy surrounding it in the July 1992 issue of the Communications of the ACM. For a response by NIST to some of the questions raised, see [SB93].
The Lamport Scheme is described in the 1976 paper by Diffie and Hellman [DH76]; the modification by Bos and Chaum is in [BC93]. The undeniable signature scheme presented in Section 6.5 is due to Chaum and van Antwerpen [CVA90]. The fail-stop signature scheme from Section 6.6 is due to van Heyst and Pedersen [VHP93].
Some examples of well-known “broken” signature schemes include the Ong-Schnorr-Shamir Scheme [OSS85] (broken by Estes et al. [EAKMM86]); and the Birational Permutation Scheme of Shamir [SH94] (broken by Coppersmith, Stern, and Vaudenay [CSV94]). Finally, ESIGN is a signature scheme due to Fujioka, Okamoto, and Miyaguchi [FOM91]. Some versions of the scheme were broken, but the variation in [FOM91] has not been broken.
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133
- Integration Strategies and Tactics for Information Technology Governance
- An Emerging Strategy for E-Business IT Governance
- Linking the IT Balanced Scorecard to the Business Objectives at a Major Canadian Financial Group
- The Evolution of IT Governance at NB Power
- Governance Structures for IT in the Health Care Industry