Cryptography: Theory and Practice:Other Public-key Cryptosystems | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

5.4 The McEliece System

The McEliece Cryptosystem uses the same design principle as the MerkleHellman Cryptosystem: decryption is an easy special case of an NP-complete problem, disguised so that it looks like a general instance of the problem. In this system, the NP-complete problem that is employed is decoding a general linear (binary) error-correcting code. However, for many special classes of codes, polynomial-time algorithms are known to exist. One such class of codes, the Goppa codes, are used as the basis of the McEliece Cryptosystem.

We begin with some essential definitions.

DEFINITION 5.4 Let k, n be positive integers, k ≤ n. An [n, k] code, C, is a k-dimensional subspace of 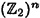, the vector space of all binary n-tuples.

A generating matrix for an [n, k] code, C, is a k × n binary matrix whose rows form a basis for C.

Let x, 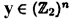, where x = (x₁, . . . , x_n) and y = (y₁ , . . . , y_n). Define the Hamming distance

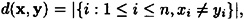
i.e., the number of coordinates in which x and y differ.

Let C be an [n, k] code. Define the distance of C to be the quantity

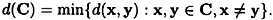
An [n, k] code with distance d is denoted as an [n, k, d] code.

The purpose of an error-correcting code is to correct random errors that occur in the transmission of (binary) data through a noisy channel. Briefly, this is done as follows. Let G be a generating matrix for an [n, k, d] code. Suppose x is the binary k-tuple we wish to transmit. Then Alice encodes x as the n-tuple y = xG, and transmits y through the channel.

Now, suppose Bob receives the n-tuple r, which may not be the same as y. He will decode r using the strategy of nearest neighbor decoding. In nearest neighbor decoding, Bob finds the codeword y′ that has minimum distance to r. Then he decodes r to y′, and, finally, determines the k-tuple x′ such that y′ = x′G. Bob is hoping that y′ = y, so x′ = x (i.e., he is hoping that any transmission errors have been corrected).

It is fairly easy to show that if at most (d - 1)/2 errors occurred during transmission, then nearest neighbor decoding does in fact correct all the errors.

Let us think about how nearest neighbor decoding would be done in practice. |C| = 2^k, so if Bob compares r to every codeword, he will have to examine 2^k vectors, which is an exponentially large number compared to k. In other words, this obvious algorithm is not a polynomial-time algorithm.

Another approach, which forms the basis for many practical decoding algorithms, is based on the idea of a syndrome. A parity-check matrix for an [n, k, d] code C having generating matrix G is an (n - k) × n 0 - 1 matrix, denoted by H, whose rows form a basis for the orthogonal complement of C, which is denoted by C⊥ and called the dual code to C. Stated another way, the rows of H are linearly independent vectors, and GH^T is a k × (n - k) matrix of zeroes.

Given a vector 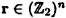, we define the syndrome of r to be Hr^T. A syndrome is a column vector with n - k components.

The following basic results follow immediately from linear algebra.

THEOREM 5.2

Suppose C is an [n, k] code with generating matrix G and parity-check matrix H. Then 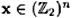is a codeword if and only if

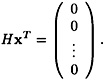
Further; if 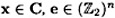, and r = x + e, then Hr^T = He^T.

Think of e as being the vector of errors that occur during transmission of a codeword x. Then r represents the vector that is received. The above theorem is saying that the syndrome depends only on the errors, and not on the particular codeword that was transmitted.

This suggests the following approach to decoding, known as syndrome decoding: First, compute s = Hr^T. If s is a vector of zeroes, then decode r as r. If not, then generate all possible error vectors or weight 1 in turn. For each such e, compute He^T. If, for any of these vectors e, it happens that He^T = s, then decode r to r - e. Otherwise, continue on to generate all error vectors of weight 2, . . . , ⌊(d - 1)/2⌋. If at any time He^T = s, then we decode r to r - e and quit. If this equation is never satisfied, then we conclude that more than ⌊(d - 1)/2⌋ errors have occurred during transmission.

By this approach, we can decode a received vector in at most

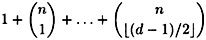
steps.

This method will work on any linear code. For certain specific types of codes, the decoding procedure can be speeded up. However, a decision version of nearest neighbor decoding is in fact an NP-complete problem. Thus no polynomial-time algorithm is known for the general problem of nearest neighbor decoding (when the number of errors is not bounded by ⌊(d - 1)/2⌋).

As was the case with the subset sum problem, we can identify an “easy” special case, and then disguise it so that it looks like a “difficult” general case of the problem. It would take us too long to go into the theory here, so we will just summarize the results. The “easy” special case that was suggested by McEliece is to use a code from a class of codes known as the Goppa codes. These codes do in fact have efficient decoding algorithms. Also, they are easy to generate, and there are a large number of inequivalent Goppa codes with the same parameters.

Table of Contents