Cryptography: Theory and Practice:Other Public-key Cryptosystems | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

The parameters of the Goppa codes have the form n = 2^m, d = 2t + 1 and k = n - mt. For a practical implementation of the public-key cryptosystem, McEliece suggested taking m = 10 and t = 50. This gives rise to a Goppa code that is a [1024, 524, 101] code. Each plaintext is a binary 524-tuple, and each ciphertext is a binary 1024-tuple. The public key is a 524 × 1024 binary matrix.

Figure 5.14 McEliece Cryptosystem

A description of the McEliece Cryptosystem is given in Figure 5.14.

We present a ridiculously small example to illustrate the encoding and decoding procedures.

Example 5.11

The matrix

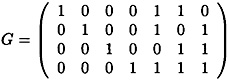
is a generating matrix for a [7, 4, 3] code, known as a Hamming code. Suppose Bob chooses the matrices

and

Then, the public generating matrix is

Now, suppose Alice encrypts the plaintext x = (1, 1, 0, 1) using as the random error vector of weight 1 the vector e = (0, 0, 0, 0, 1, 0, 0). The ciphertext is computed to be

When Bob receives the ciphertext y, he first computes

Next, he decrypts y₁ to get x₁ = (1, 0, 0, 0, 1, 1, 0) (note that e₁ ≠ e due to the multiplication by P^-1).

Next, Bob forms x₀ = (1, 0, 0, 0) (the first four components of x₁).

Finally, Bob calculates

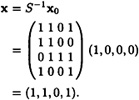
This is indeed the plaintext that Alice encrypted.

5.5 Notes and References

The ElGamal Cryptosystem was presented in [EL85]. The Pohlig-Hellman algorithm was published in [PH78], and the material concerning individual bits of the Discrete Logarithm problem is based on Peralta [PE86]. For further information on the Discrete Logarithm problem, we recommend the articles by LaMacchia and Odlyzko [LO91] and McCurley [MC90].

The main reference book for finite fields is Lidl and Niederreiter [LN83]. McEliece [MC87] is a good textbook on the subject, and a research monograph on applications of finite fields was published by Menezes et al. [MBGMVY93]. A recent article on the Discrete Logarithm problem in GF(2ⁿ) is Gordon and McCurley [GM93].

The idea of using elliptic curves for public-key cryptosystems is due to Koblitz [KO87] and Miller [MI86]. Menezes [ME93] is a monograph on elliptic curve cryptosystems. See also Menezes and Vanstone [MV93] and Koblitz [KO94]. For an elementary treatment of elliptic curves, see Silverman and Tate [ST92]. The Menezes-Okamoto-Vanstone reduction of discrete logarithms from elliptic curves to finite fields is given in [MOV94] (see also [ME93]).

The Merkle-Hellman Cryptosystem was presented in [MH78]. This system was broken by Shamir [SH84], and the “iterated” version of the system was broken by Brickell [BR85]. A different knapsack-type system, due to Chor and Rivest [CR88], has not been broken. For more information, see the survey article by Brickell and Odlyzko [BO92].

The most important reference book for coding theory is MacWilliams and Sloane [MS77] There are many good textbooks on coding theory, e.g., Hoffman et al. [HLLPRW91] and Vanstone and van Oorschot [VV89]. The McEliece Cryptosystem was first described in [MC78]. A recent article discussing the security of this cryptosystem is by Chabaud [CH95].

Exercises

5.1 Implement Shanks’ algorithm for finding discrete logarithms in

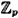, where p is prime and α is a primitive element. Use your program to find log₁₀₆ 12375 in

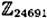and log₆ 248388 in

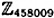5.2 Implement the Pohlig-Hellman algorithm for finding discrete logarithms in

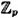, where p is prime and α is a primitive element. Use your program to find log₅ 8563 in

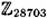and log₁₀ 12611 in

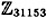5.3 Find log₅ 896 in

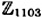using the algorithm presented in Figure 5.6, given that L₂(β) = 1 for β = 25, 219 and 841, and L₂(β) = 0 for β = 163, 532, 625 and 656.

5.4 Decrypt the ElGamal ciphertext presented in Table 5.3. The parameters of the system arc p = 31847, α = 5, a = 7899 and β = 18074. Each element of

represents three alphabetic characters as in Exercise 4.6.

The plaintext was taken from “The English Patient,” by Michael Ondaatje, Alfred A. Knopf, Inc., New York, 1992.

5.5 Determine which of the following polynomials are irreducible over

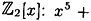5.6 The field GF(2⁵) can be constructed as

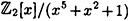. Perform the following computations in this field.

(a) Compute (x⁴ + x²) × (x³ + x + 1).

(b) Using the extended Euclidean algorithm, compute (x³ + x²)^-1

5.7 We give an example of the ElGamal Cryptosystem implemented in GF(3³). The polynomial x³+2x²+1 is irreducible over

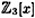and hence

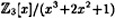is the field GF(3³). We can associate the 26 letters of the alphabet with the 26 nonzero field elements, and thus encrypt ordinary text in a convenient way. We will use a lexicographic ordering of the (nonzero) polynomials to set up the correspondence. This correspondence is as follows: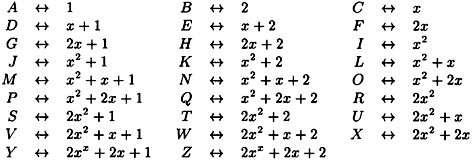

Suppose Bob uses α = x and a = 11 in an ElGamal system; then β = x + 2. Show how Bob will decrypt the following string of ciphertext:

(K, H) (P X) (N, K) (H,R) (T,F) (V, Y) (E, H) (F, A) (T, W) (J, D)(U, J)

**Table 5.3** ElGamal Ciphertext
(3781, 14409)	(31552, 3930)	(27214, 15442)	(5809, 30274)
(54000, 31486)	(19936, 721)	(27765, 29284)	(29820, 7710)
(31590, 26470)	(3781, 14409)	(15898, 30844)	(19048, 12914)
(16160, 3129)	(301, 17252)	(24689, 7776)	(28856, 15720)
(30555, 24611)	(20501, 2922)	(13659, 5015)	(5740, 31233)
(1616, 14170)	(4294, 2307)	(2320, 29174)	(3036, 20132)
(14130, 22010)	(25910, 19663)	(19557, 10145)	(18899, 27609)
(26004, 25056)	(5400, 31486)	(9526, 3019)	(12962, 15189)
(29538, 5408)	(3149, 7400)	(9396, 3058)	(27149, 20535)
(1777, 8737)	(26117, 14251)	(7129, 18195)	(25302, 10248)
(23258, 3468)	(26052, 20545)	(21958, 5713)	(346, 31194)
(8836, 25898)	(8794, 17358)	(1777, 8737)	(25038, 12483)
(10422, 5552)	(1777, 8737)	(3780, 16360)	(11685, 133)
(25115, 10840)	(14130, 22010)	(16081, 16414)	(28580, 20845)
(23418, 22058)	(24139, 9580)	(173, 17075)	(2016, 18131)
(198886, 22344)	(21600, 25505)	(27119, 19921)	(23312, 16906)
(21563, 7891)	(28250, 21321)	(28327, 19237)	(15313, 28649)
(24271, 8480)	(26592, 25457)	(9660, 7939)	(10267, 20623)
(30499, 14423)	(5839, 24179)	(12846, 6598)	(9284, 27858)
(24875, 17641)	(1777, 8737)	(18825, 19671)	(31306, 11929)
(3576, 4630)	(26664, 27572)	(27011, 29164)	(22763, 8992)
(3149, 7400)	(8951, 29435)	(2059, 3977)	(16258, 30341)
(21541, 19004)	(5865, 29526)	(10536, 6941)	(1777, 8737)
(17561, 11884)	(2209, 6107)	(10422, 5552)	(19371, 21005)
(26521, 5803)	(14884, 14280)	(4328, 8635)	(28250, 21321)
(28327, 19237)	(15313, 28649)

5.8 Let E be the elliptic curve y² = x³ + x + 28 defined over

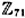(a) Determine the number of points on E.

(b) Show that E is not a cyclic group.

5.9 Let E be the elliptic curve y² = x³ + x + 13 defined over

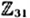. It can be shown that #E = 34 and (9, 10) is an element of order 34 in E. The Menezes-Vanstone Cryptosystem defined on E will have as its plaintext space

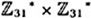. Suppose Bob’s secret exponent is a = 25.

(a) Compute β = aα.

(b) Decrypt the following string of ciphertext:

((4, 9), 28, 7), ((19, 28), 9, 13), ((5,22), 20, 17), ((25, 16), 12, 27).

(c) Assuming that each plaintext represents two alphabetic characters, convert the plaintext into an English word. (Here we will use the correspondence A ↔ 1, . . . , Z ↔ 26, since 0 is not allowed in a (plaintext) ordered pair.)

5.10 Suppose the Merkle-Hellman Cryptosystem has as its public list of sizes the vector

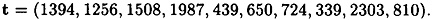
Suppose Oscar discovers that p = 2503.

(a) By trial and error, determine the value a such that the list a^-1t mod p is a permutation of a superincreasing list.

(b) Show how the ciphertext 5746 would be decrypted.

5.11 It can be shown that the matrix H shown below is a parity-check matrix for a [15, 7, 5] code called a BCH code.

Decode, it possible, each of the following received vectors r using the syndrome decoding method.

(a) r = (1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0).

(b) r = (1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0).

Table of Contents