Cryptography: Theory and Practice:The RSA System and Factoring
 | Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210 Pub Date: 03/17/95 |
| Previous | Table of Contents | Next |
4.9 Notes and References
The idea of public-key cryptography was introduced by Diffie and Hellman in 1976. Although [DH76A] is the most cited reference, the conference paper [DH76] actually appeared a bit earlier. The RSA Cryptosystem was discovered by Rivest, Shamir and Adleman [RSA78]. The Rabin Cryptosystem was described in Rabin [RA79]; a similar provably secure system in which decryption is unambiguous was found by Williams [WI80]. For a general survey article on public-key cryptography, we recommend Diffie [DI92].
The Solovay-Strassen test was first described in [SS77]. The Miller-Rabin test was given in [MI76] and [RA80]. Our discussion of error probabilities is motivated by observations of Brassard and Bratley [BB88A, §8.6] (see also [BBCGP88]). The best current bounds on the error probability of the Miller-Rabin algorithm can be found in [DLP93].
The material in Section 4.6 is based on the treatment by Salomaa [SA90, pp. 143-154]. The factorization of n given the decryption exponent was proved in [DE84]; the results on partial information revealed by RSA is from [GMT82].
As mentioned earlier, there are many sources of information on factoring algorithms. Pomerance [PO90] is a good survey on factoring, and Lenstra and Lenstra [LL90] is a good article on number-theoretic algorithms in general. Bressoud [BR89] is an elementary textbook devoted to factoring and primality testing. Cryptography textbooks that emphasize number theory include Koblitz [KO94] and Kranakis [KR86]. Lenstra and Lenstra [LL93] is a monograph on the number field sieve.
Exercises 4.7-4.9 give some examples of protocol failures. For a nice article on this subject, see Moore [MO92].
Exercises
- 4.1 Use the Extended Euclidean algorithm to compute the following multiplicative inverses:
- (a) 17-1 mod 101
- (b) 357-1 mod 1234
- (c) 3125-1 mod 9987.
- (b) 357-1 mod 1234
- 4.2 Solve the following system of congruences:

- 4.3 Solve the following system of congruences:

HINT First use the Extended Euclidean algorithm, and then apply the Chinese remainder theorem.
- 4.4 Here we investigate some properties of primitive roots.
- (a) The integer 97 is prime. Prove that x ± 0 is a primitive root modulo 97 if and only if
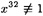 (mod 97) and
(mod 97) and  (mod 97).
(mod 97).- (b) Use this method to find the smallest primitive root modulo 97.
- (c) Suppose p is prime, and p - 1 has prime power factorization
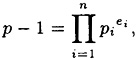
where the pi’s are distinct primes. Prove that x ± 0 is a primitive root modulo p if and only if
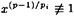 (mod p) for 1 ≤ i ≤ n.
(mod p) for 1 ≤ i ≤ n. - (b) Use this method to find the smallest primitive root modulo 97.
- 4.5 Suppose that n = pq, where p and q are distinct odd primes and ab ≡ 1 (mod (p -1)(q - 1)). The RSA encryption operation is e(x) = xb mod n and the decryption operation is d(y) = ya mod n. We proved that d(e(x)) = x if
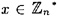 . Prove that the same statement is true for any
. Prove that the same statement is true for any 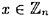 .
.HINT Use thr fact that x1 ≡ x2 (mod pq) if and only if x1 ≡ x2 (mod p) and x1 ≡ x2 (mod q). This follows from the Chinese remainder theorem.
- 4.6 Two samples of RSA ciphertext are presented in Tables 4.1 and 4.2. Your task is to decrypt them. The public parameters of the system are n = 18923 and b = 1261 (for Table 4.1) and n = 31313 and b = 4913 (for Table 4.2). This can be accomplished as follows. First, factor n (which is easy because it is so small). Then compute the exponent a from φ(n), and, finally, decrypt the ciphertext. Use the square-and-multiply algorithm to exponentiate modulo n.
In order to translate the plaintext back into ordinary English text, you need to know how alphabetic characters are “encoded” as elements in
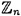 . Each element of
. Each element of - (a) 17-1 mod 101
| 12423 | 11524 | 7243 | 7459 | 14303 | 6127 | 10964 | 16399 |
| 9792 | 13629 | 14407 | 18817 | 18830 | 13556 | 3159 | 16647 |
| 5300 | 13951 | 81 | 8986 | 8007 | 13167 | 10022 | 17213 |
| 2264 | 961 | 17459 | 4101 | 2999 | 14569 | 17183 | 15827 |
| 12693 | 9553 | 18194 | 3830 | 2664 | 13998 | 12501 | 18873 |
| 12161 | 13071 | 16900 | 7233 | 8270 | 17086 | 9792 | 14266 |
| 13236 | 5300 | 13951 | 8850 | 12129 | 6091 | 18110 | 3332 |
| 15061 | 12347 | 7817 | 7946 | 11675 | 13924 | 13892 | 18031 |
| 2620 | 6276 | 8500 | 201 | 8850 | 11178 | 16477 | 10161 |
| 3533 | 13842 | 7537 | 12259 | 18110 | 44 | 2364 | 15570 |
| 3460 | 9886 | 8687 | 4481 | 11231 | 7547 | 11383 | 17910 |
| 12867 | 13203 | 5102 | 4742 | 5053 | 15407 | 2976 | 9330 |
| 12192 | 56 | 2471 | 15334 | 841 | 13995 | 17592 | 13297 |
| 2430 | 9741 | 11675 | 424 | 6686 | 738 | 13874 | 8168 |
| 7913 | 6246 | 14301 | 1144 | 9056 | 15967 | 7328 | 13203 |
| 796 | 195 | 9872 | 16979 | 15404 | 14130 | 9105 | 2001 |
| 9792 | 14251 | 1498 | 11296 | 1105 | 4502 | 16979 | 1105 |
| 56 | 4118 | 11302 | 5988 | 3363 | 15827 | 6928 | 4191 |
| 4277 | 10617 | 874 | 13211 | 11821 | 3090 | 18110 | 44 |
| 2364 | 15570 | 3460 | 9886 | 9988 | 3798 | 1158 | 9872 |
| 16979 | 15404 | 6127 | 9872 | 3652 | 14838 | 7437 | 2540 |
| 1367 | 2512 | 14407 | 5053 | 1521 | 297 | 10935 | 17137 |
| 2186 | 9433 | 13293 | 7555 | 13618 | 13000 | 6490 | 5310 |
| 18676 | 4782 | 11374 | 446 | 4165 | 11634 | 3846 | 14611 |
| 2364 | 6789 | 11634 | 4493 | 4063 | 4576 | 17955 | 7965 |
| 11748 | 14616 | 11453 | 17666 | 925 | 56 | 4118 | 18031 |
| 9522 | 14838 | 7437 | 3880 | 11476 | 8305 | 5102 | 2999 |
| 18628 | 14326 | 9175 | 9061 | 650 | 18110 | 8720 | 15404 |
| 2951 | 722 | 15334 | 841 | 15610 | 2443 | 11056 | 2186 |
-
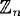 represents three alphabetic characters as in the following examples:
represents three alphabetic characters as in the following examples: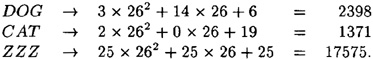
You will have to invert this process as the final step in your program.
The first plaintext was taken from “The Diary of Samuel Marchbanks,” by Robertson Davies, 1947, and the second was taken from “Lake Wobegon Days,” by Garrison Keillor, 1985.
- 4.7 This exercise exhibits what is called a protocol failure. It provides an example where ciphertext can be decrypted by an opponent, without determining the key, if a cryptosystem is used in a careless way. (Since the opponent does not determine the key, it is not accurate to call it cryptanalysis.) The moral is that it is not sufficient to use a “secure” cryptosystem in order to guarantee “secure” communication.
Suppose Bob has an RSA Cryptosystem with a large modulus n for which the factorization cannot be found in a reasonable amount of time. Suppose Alice sends
- 4.7 This exercise exhibits what is called a protocol failure. It provides an example where ciphertext can be decrypted by an opponent, without determining the key, if a cryptosystem is used in a careless way. (Since the opponent does not determine the key, it is not accurate to call it cryptanalysis.) The moral is that it is not sufficient to use a “secure” cryptosystem in order to guarantee “secure” communication.
| 6340 | 8309 | 14010 | 8936 | 27358 | 25023 | 16481 | 25809 |
| 23614 | 7135 | 24996 | 30590 | 27570 | 26486 | 30388 | 9395 |
| 27584 | 14999 | 4517 | 12146 | 29421 | 26439 | 1606 | 17881 |
| 25774 | 7647 | 23901 | 7372 | 25774 | 18436 | 12056 | 13547 |
| 7908 | 8635 | 2149 | 1908 | 22076 | 7372 | 8686 | 1304 |
| 4082 | 11803 | 5314 | 107 | 7359 | 22470 | 7372 | 22827 |
| 15698 | 30317 | 4685 | 14696 | 30388 | 8671 | 29956 | 15705 |
| 1417 | 26905 | 25809 | 28347 | 26277 | 7897 | 20240 | 21519 |
| 12437 | 1108 | 27106 | 18743 | 24144 | 10685 | 25234 | 30155 |
| 23005 | 8267 | 9917 | 7994 | 9694 | 2149 | 10042 | 27705 |
| 15930 | 29748 | 8635 | 23645 | 11738 | 24591 | 20240 | 27212 |
| 27486 | 9741 | 2149 | 29329 | 2149 | 5501 | 14015 | 30155 |
| 18154 | 22319 | 27705 | 20321 | 23254 | 13624 | 3249 | 5443 |
| 2149 | 16975 | 16087 | 14600 | 27705 | 19386 | 7325 | 26277 |
| 19554 | 23614 | 7553 | 4734 | 8091 | 23973 | 14015 | 107 |
| 3183 | 17347 | 25234 | 4595 | 21498 | 6360 | 19837 | 8463 |
| 6000 | 31280 | 29413 | 2066 | 369 | 23204 | 8425 | 7792 |
| 25973 | 4477 | 30989 |
-
a message to Bob by representing each alphabetic character as an integer between 0 and 25 (i.e., A ↔ 0, B ↔ 1, etc.), and then encrypting each residue modulo 26 as a separate plaintext character.
- (a) Describe how Oscar can easily decrypt a message which is encrypted in this way.
- (b) Illustrate this attack by decrypting the following ciphertext (which was encrypted using an RSA Cryptosystem with n = 18721 and b = 25) without factoring the modulus:
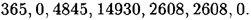
- (b) Illustrate this attack by decrypting the following ciphertext (which was encrypted using an RSA Cryptosystem with n = 18721 and b = 25) without factoring the modulus:
- 4.8 This exercise illustrates another example of a protocol failure (due to Simmons) involving RSA; it is called the common modulus protocol failure. Suppose Bob has an RSA Cryptosystem with modulus n and decryption exponent b1, and Charlie has an RSA Cryptosystem with (the same) modulus n and decryption exponent b2. Suppose also that gcd(b1, b2) = 1. Now, consider the situation that arises if Alice encrypts the same plaintext x to send to both Bob and Charlie. Thus, she computes
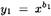 mod n and
mod n and 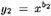 mod n, and then she sends y1 to Bob and y2 to Charlie. Suppose Oscar intercepts y1 and y2, and performs the computations indicated in Figure 4.16.
mod n, and then she sends y1 to Bob and y2 to Charlie. Suppose Oscar intercepts y1 and y2, and performs the computations indicated in Figure 4.16. - (a) Prove that the value x1 computed in step 3 of Figure 4.16 is in fact Alice’s plaintext, x. Thus, Oscar can decrypt the message Alice sent, even though the cryptosystem may be “secure.”
- (b) Illustrate the attack by computing x by this method if n = 18721, b1 = 43, b2 = 7717, y1 = 12677 and y2 = 14702.
- 4.9 We give yet another protocol failure involving RSA. Suppose that three users in a network, say Bob, Bart and Bert, all have public encryption exponents b = 3.

Figure 4.16 RSA common modulus protocol failureLet their moduli be denoted by n1, n2, n3. Now suppose Alice encrypts the same plaintext x to send to Bob, Bart and Bert. That is, Alice computes yi = x3 mod ni, 1 ≤ i ≤ 3. Describe how Oscar can compute x, given y1, y2 and y3, without factoring any of the moduli.
- 4.10 A plaintext x is said to be fixed if eK(x) = x. Show that, for the RSA Cryptosystem, the number of fixed plaintexts
 is equal to gcd(b - 1, p - 1) × gcd(b -1, q - 1).
is equal to gcd(b - 1, p - 1) × gcd(b -1, q - 1). HINT Consider the system of two congruences eK(x) ≡ x (mod p), eK(x) ≡ x (mod q).
- 4.11 Suppose A is a deterministic algorithm which is given as input an RSA modulus n, an encryption exponent b, and a ciphertext y. A will either decrypt y or return no answer. Supposing that there are ∈(n - 1) ciphertexts which A is able to decrypt, show how to use A as an oracle in a Las Vegas decryption algorithm having success probability ∈.
HINT Use the multiplicative property of RSA that eK(x1)eK(x2) = eK(x1x2), where all arithmetic operations are modulo n.
- 4.12 Write a program to evaluate Jacobi symbols using the four properties presented in Section 4.5. The program should not do any factoring, other than dividing out powers of two. Test your program by computing the following Jacobi symbols:
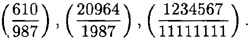
- 4.13 For n = 837, 851 and 1189, find the number of bases 6 such that n, is an Euler pseudo-prime to the base b.
- 4.14 The purpose of this question is to prove that the error probability of the Solovay-Strassen primality test is at most 1/2. Let
 denote the group of units modulo n. Define
denote the group of units modulo n. Define - (a) Prove that G(n) is a subgroup of
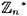 . Hence, by Lagranges theorem, if
. Hence, by Lagranges theorem, if 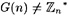 , then
, then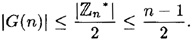
- (b) Suppose n = pk q, where p and q are odd, p is prime, k ≥ 2, and gcd(p, q) = 1. Let a = 1 + pk-1 q. Prove that
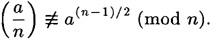
HINT Use the binomial theorem to compute a(n-1)/2.
- (c) Suppose n = p1, . . . ps, where the pi’s are distinct odd primes. Suppose a ≡ u (mod p1) and a ≡ 1 (mod p2p3 . . . ps), where u is a quadratic non-residue modulo p1 (note that such an a exists by the Chinese remainder theorem). Prove that

but
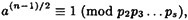
so
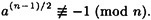
- (d) If n is odd and composite, prove that |G(n)| ≤ (n - 1)/2.
- (e) Summarize the above: prove that the error probability of the Solovay-Strassen primality test is at most 1/2.
- (b) Suppose n = pk q, where p and q are odd, p is prime, k ≥ 2, and gcd(p, q) = 1. Let a = 1 + pk-1 q. Prove that
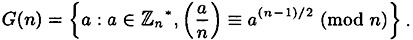
- 4.15 Suppose we have a Las Vegas algorithm with failure probability ∈.
- (a) Prove that the probability of first achieving success on the nth trial is pn = ∈n-1(1 - ∈).
- (b) The average (expected) number of trials to achieve success is
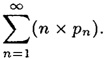
Show that this average is equal to 1/(1 - ∈).
- (c) Let δ be a positive real number less than 1. Show that the number of iterations required in order to reduce the probaility of failure to at most δ is
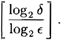
- (b) The average (expected) number of trials to achieve success is
- 4.16 Suppose Bob has carelessly revealed his decryption exponent to be a = 14039 in an RSA Cryptosystem with public key n = 36581 and b = 4679. Implement the probablistic algorithm to factor n given this information. Test your algorithm with the “random” choices w = 9983 and w = 13461. Show all computations.
- 4.17 Prove Equations 4.1 and 4.2 relating the functions half and parity.
- 4.18 Suppose p = 199, q = 211 and B = 1357 in the Rabin Cryptosystem. Perform following computations.
- (a) Determine the four square roots of 1 modulo n, where n = pq.
- (b) Compute the encryption y = eK (32767).
- (c) Determine the four possible decryptions of this given ciphertext y.
- (b) Compute the encryption y = eK (32767).
- 4.19 Factor 262063 and 9420457 using the p - 1 method. How big does B have to be in each case to be successful?
- (a) Describe how Oscar can easily decrypt a message which is encrypted in this way.
| Previous | Table of Contents | Next |
Copyright © CRC Press LLC
EAN: 2147483647
Pages: 133