Cryptography: Theory and Practice:Other Public-key Cryptosystems

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210   Pub Date: 03/17/95  

Previous

Table of Contents

Next

Chapter 5
Other Public-key Cryptosystems

In this chapter, we look at several other public-key cryptosystems. The ElGamal Cryptosystem is based on the Discrete Logarithm problem, which we will have occasion to use in numerous cryptographic protocols throughout the rest of the text. Thus we devote a considerable amount of time to discussion of this important problem. In later sections, we give relatively brief treatments of some other well-known public-key cryptosystems. These include ElGamal-type systems based on finite fields and elliptic curves, the (broken) Merkle-Hellman Knapsack Cryptosystem and the McEliece Cryptosystem.

5.1 The ElGamal Cryptosystem and Discrete Logs

The ElGamal Cryptosystem is based on the Discrete Logarithm problem. We begin by describing this problem in the setting of a finite field 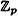, where p is prime, in Figure 5.1. (Recall that the multiplicative group 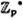is cyclic, and a generator of 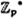is called a primitive element.)

The Discrete Logarithm problem in 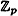has been the object of much study. The problem is generally regarded as being difficult if p is carefully chosen. In particular, there is no known polynomial-time algorithm for the Discrete Logarithm problem. To thwart known attacks, p should have at least 150 digits, and p - 1 should have at least one “large” prime factor. The utility of the Discrete Logarithm problem in a cryptographic setting is that finding discrete logs is (probably) difficult, but the inverse operation of exponentiation can be computed efficiently by using the square-and-multiply method described earlier. Stated another way, exponentiation modulo p is a one-way function for suitable primes p.

ElGamal has developed a public-key cryptosystem based on the Discrete Logarithm problem. This system is presented in Figure 5.2.

The ElGamal Cryptosystem is non-deterministic, since the ciphertext depends on both the plaintext x and on the random value k chosen by Alice. So there will be many ciphertexts that are encryptions of the same plaintext.

Figure 5.1  The discrete logarithm problem in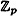

Figure 5.2  ElGamal Public-key Cryptosystem in

Informally, this is how the ElGamal Cryptosystem works. The plaintext x is “masked” by multiplying it by β^k, yielding y₂. The value α^k is also transmitted as part of the ciphertext. Bob, who knows the secret exponent a, can compute β^k from β^k. Then he can “remove the mask” by dividing y₂ by β^k to obtain x.

A small example will illustrate.

Example 5.I

Suppose p = 2579, α = 2, a = 765, and hence

Now, suppose that Alice wishes to send the message x = 1299 to Bob. Say k = 853 is the random integer she chooses. Then she computes

and

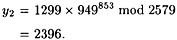
When Bob receives the ciphertext y = (435, 2396), he computes

which was the plaintext that Alice encrypted.

5.1.1 Algorithms for the Discrete Log Problem

Throughout this section, we assume that p is prime and a is a primitive element modulo p. We take p and α to be fixed. Hence the Discrete Logarithm problem can be phrased in the following form: Given 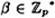, find the unique exponent a, 0 ≤ a ≤ p - 2, such that α^a ≡ β (mod p).

Clearly, the Discrete Logarithm problem can be solved by exhaustive search in O(p) time and O(1) space (neglecting logarithmic factors). By precomputing all possible values α^a, and sorting the ordered pairs (a, α^a mood p) with respect to their second coordinates, we can solve the discrete log problem in O(1) time with O(p) precomputation and O(p) memory (again, neglecting logarithmic factors). The first non-trivial algorithm we describe is a time-memory trade-off due to Shanks.

Figure 5.3  Shanks’ algorithm for the discrete logarithm problem

Shanks’ Algorithm

Denote 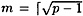. Shanks’ algorithm is presented in Figure 5.3. Some comments are in order. First, steps 1 and 2 can be precomputed, if desired (this will not affect the asymptotic running time, however). Next, observe that if (j, y) ∈ L₁ and (i, y) ∈ L₂, then

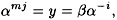
so

as desired. Conversely, for any β, we can write

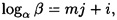
where 0 ≤ j,i ≤ m - 1. Hence, the search in step 5 will be successful.

It is not difficult to implement the algorithm to run in O(m) time with O(m) memory (neglecting logarithmic factors). Note that step 5 can be done with one (simultaneous) pass through each of the two lists L₁ and L₂.

Here is a small example to illustrate.

Example 5.2

Suppose p = 809, and we wish to find log₃ 525. So we have α = 3, β = 525 and 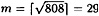. Then

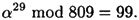
First, we compute the ordered pairs (j, 99^j mod 809) for 0 ≤ j ≤ 28. We obtain the list

(0, 1)	(1, 99)	(2, 93)	(3, 308)	(4, 559)
(5, 329)	(6, 211)	(7, 664)	(8, 207)	(9, 268)
(10, 644)	(11, 654)	(12, 26)	(13, 147)	(14, 800)
(15, 727)	(16, 781)	(17, 464)	(18, 632)	(19, 275)
(20, 528)	(21, 496)	(22, 564)	(23, 15)	(24, 676)
(25, 586)	(26, 575)	(27, 295)	(28, 81)

which is then sorted to produce L₁.

Previous

Table of Contents

Next

---

Copyright © CRC Press LLC