Cryptography: Theory and Practice:Other Public-key Cryptosystems | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

The second list contains the ordered pairs (i, 525 × (3ⁱ)^-1 mod 809), 0 ≤ j ≤ 28. It is as follows:

(0, 525)	(1, 175)	(2, 328)	(3, 379)	(4, 396)
(5, 132)	(6, 44)	(7, 554)	(8, 724)	(9, 511)
(10, 440)	(11, 686)	(12, 768)	(13, 256)	(14, 355)
(15, 388)	(16, 399)	(17, 133)	(18, 314)	(19, 644)
(20, 754)	(21, 521)	(22, 713)	(23, 777)	(24, 259)
(25, 356)	(26, 658)	(27, 489)	(28, 163)

After sorting this list, we get L₂.

Now, if we proceed simultaneously through the two sorted lists, we find that (10, 644) is in L₁ and (19, 644) is in L₂. Hence, we can compute

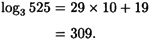
As a check, it can be verified that indeed 3³⁰⁹ ≡ 525 (mod 809).

The Pohlig-Hellman Algorithm

The next algorithm we study is the Pohlig-Hellman algorithm. Suppose

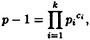
where the P_i’s are distinct primes. The value a = log_α β is determined (uniquely) modulo p - 1. We first observe that if we can compute a mod 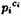for each i, 1 ≤ i ≤ k, then we can compute a mod (p - 1) by the Chinese remainder theorem. So, let’s suppose that q is prime,

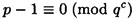
and

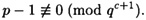
We will show how to compute the value

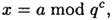
where 0 ≤ x ≤ q^c - 1. We can express x in radix q representation as

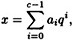
where 0 ≤ a_i ≤ q - 1 for 0 ≤ i ≤ c - 1. Also, observe that we can express a as

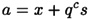
for some integer s.

The first step of the algorithm is to compute a₀. The main observation is that

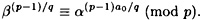
To see this, note that

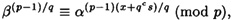
so it suffices to show that

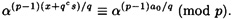
This will be true if and only if

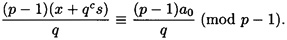
However, we have

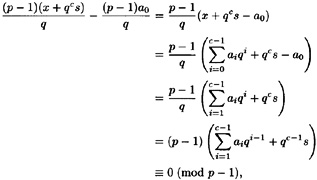
which was what we wanted to prove.

Hence, we begin by computing β^(p-1)/q mod p. If

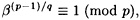
then a₀ = 0. Otherwise, we successively compute

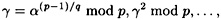
until

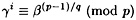
for some i. When this happens, we have a₀ = i.

Now, if c = 1, we’re done. Otherwise c > 1, and we proceed to determine a₁. To do this, we define

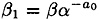
and denote

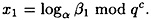
It is not hard to see that

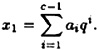
Hence, it follows that

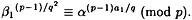
So, we will compute β₁^(p-1)/q2 mod p, and then find i such that

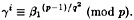
Then we have a₁ = i.

If c = 2, we are now finished; otherwise, we repeat this process c - 2 more times, obtaining a₂,..., a_c-1.

A pseudo-code description of the Pohlig-Hellman algorithm is given in Figure 5.4. In this algorithm, α is a primitive element modulo p, q is prime,

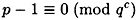
and

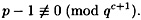
The algorithm calculates a₀,..., a_c-1, where

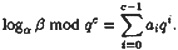
We illustrate the Pohlig-Hellman algorithm with a small example.

Figure 5.4 Pohlig-Hellman algorithm to compute log_αβ mod q^c

Example 5.3

Suppose p = 29; then

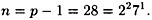
Suppose α = 2 and β = 18, so we want to determine a = log₂ 18. We proceed by first computing a mod 4 and then computing a mood 7.

We start by setting q = 2 and c = 2. First,

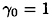
and

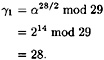
Next,

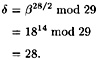
Hence, a₀ = 1. Next, we compute

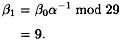
and

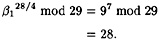
Since

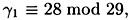
we have a₁ = 1. Hence, a ≡ 3 (mod 4).

Next, we set q = 7 and c = 1. We have

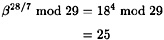
and

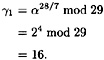
Then we would compute

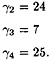
Hence, a₀ = 4 and a ≤ 4 (mod 7).

Finally, solving the system

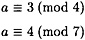
using the Chinese remainder theorem, we get a ≡ 11 (mod 28). That is, we have computed log₂ 18 in 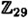to be 11.

The Index Calculus Method

The index calculus method for computing discrete logs bears considerable resemblence to many of the best factoring algorithms. We give a very brief overview in this section. The method uses a factor base, which, as before, is a set 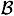of “small” primes. Suppose 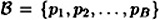. The first step (a preprocessing step) is to find the logarithms of the B primes in the factor base. The second step is to compute a discrete log of a desired element β, using the knowledge of the discrete logs of the elements in the factor base.

In the precomputation, we construct C = B + 10 congruences modulo p, as follows:

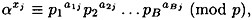
1 ≤ j ≤ C. Notice these congruences can be written equivalently as

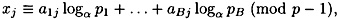
1 ≤ j ≤ C. Given C congruences in the B “unknowns” log_α p_i (1 ≤ i ≤ B), we hope that there is a unique solution modulo p - 1. If this is the case, then we can compute the logarithms of the elements in the factor base.

How do we generate congruences of the desired form? One elementary way is to take a random value x, compute a^x mod p, and then determine if a^x mod p has all its factors in 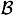(using trial division, for example).

Table of Contents