5.1 Analytical versus Computer Solutions
5.1 Analytical versus Computer Solutions If the function is linear, then there is at most one root, and we can easily find it analytically with simple algebra. For example, if then we just have to "do the math": So 2 is the root of the function 3 x - 6, and finding it is the solution to the problem "Solve the equation 3 x = 6 for x. " There are even formulas for roots. For the quadratic function f ( x ) = ax 2 + bx + c, where a, b, and c are real, and a to obtain the roots. If the discriminant b 2 - 4 ac is positive, the two roots are real and unequal . If it's 0, the two roots are real and equal, and if it's negative, the two roots are complex. If the function f is a general polynomial, we may be able to solve it by factoring. For example, if then we can factor it to and so x = 1, x = 3, and x = 2 are all roots. But how do we program the computer to find roots? An analytical solution, such as by factoring and other algebraic manipulations, is fine to do by hand but difficult to program. The quadratic formula is easy to code, but it's only for quadratic functions. The algorithms in this chapter take advantage of a computer's computational speed?athey use brute force to find real roots iteratively by using trial and error. If we apply such algorithms intelligently, we'll maximize the chances that the trial x values (the successive approximations ) converge to a root, and converge quickly. We hope that each trial decreases the error. For each algorithm, we'll first write a simple program that illustrates the technique by printing out the successive approximations to a function's root. Next, we'll use an interactive program that animates the algorithm for a set of functions. You select the function, and then by clicking and dragging the mouse, you can set the value of the first trial value for x and watch the program converge (or fail to converge) to a root of the function. |
| |
| Top |
EAN: 2147483647
Pages: 141

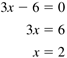
 0, we can use the quadratic formula we saw in Chapter 1
0, we can use the quadratic formula we saw in Chapter 1