8.8 Approximations for Reciprocals and Square Roots
| The IEEE floating-point standard defines requirements for the operations of division and remainder and for the unary square root function, including cases where source arguments are IEEE special values (zeros, infinities, NaN, etc.). Some RISC architectures include full hardware support for floating-point division and the square root function; these operations take more CPU cycles than other floating-point arithmetic operations and thus tend to cause pipeline stalls. The designers of the Itanium architecture took a different approach, utilizing lookup tables that provide approximations for reciprocals and reciprocal square roots, with known bounds on accuracy. These lookups execute in the same number of CPU cycles as the fma instruction, and can be followed by software instruction sequences that refine the approximations, using series expansions to compute a result with the desired accuracy. The parallelism inherent in this EPIC architecture allows performance comparable to, or perhaps superior to, that of the typical hardware-only approaches of RISC architectures. The Itanium approximation instructions themselves handle the IEEE special cases, thus permitting the follow-up sequences of software instructions to execute along a uniform algorithmic path. Markstein and others have written extensively on this topic, while we briefly sketch the mathematical analysis just enough to demonstrate the use of these instructions in the context of the architecture. 8.8.1 Floating-Point Reciprocal ApproximationThe floating-point reciprocal approximation instruction uses two source registers and two destination registers to compute either an approximate reciprocal or an IEEE-mandated quotient: frcpa.sf f1,p2=f2,f3 // usually p2=1 and f1 = 1 / f3 // or p2=0 and f1 = f2 / f3 // (IEEE-mandated quotients) // or p2=0 (other conditions) where sf (the status field completer) can have the same values as those given previously (Section 8.4.1) for arithmetic operations. If the qualifying predicate of the frcpa instruction is zero, then predicate register p2 is cleared to zero and register f1 is left unchanged. If either source register contains NaTVal, then register f1 is set to NaTVal and predicate register p2 is cleared to zero. The frcpa instruction uses the leading bits <62:55> from the significand in register f3 as the index into a 256-entry lookup table. The significand in destination register f1 is given the value 1 in bit <63>, the 10-bit result in bits <62:53>, and 0 in bits <52:0>. The exponent is determined appropriately from the exponent field in the f3 source. The result has the same sign as the source. This approximation has a known accuracy of at least 8.886 valid bits when compared to the mathematically precise reciprocal. In order to demonstrate how the frcpa instruction is used to compute a refined result (following Markstein), suppose that y0 is the tabular approximation of the exact reciprocal of some value b. The relative error of approximating b 1 by y0 is
Rearranging this definition of e0 can improve the approximations to b 1:
This sequence converges, since we know that e0 To see the efficiency of this strategy, we can choose the rather obvious first-order correction y1 = y0 + y0e0 and recalculate the new relative error e1 as
which can be simplified as
The number of valid bits doubles with each successive refinement, y0, y1, …. Markstein emphasizes that the properties of Itanium fused floating-point instructions contribute to the well-analyzed, provable accuracy of successive approximations by curtailing loss of accuracy in calculating e0 from b and y0, and then y1, y2, …. 8.8.2 Reciprocal Square Root ApproximationThe floating-point reciprocal square root approximation instruction uses one source register and two destination registers to compute either an approximate reciprocal square root or an IEEE-mandated square root: frsqrta.sf f1,p2=f3 // usually p2=1 and f1 = 1 / sqr(f3) // or p2=0 and f1 = sqr(f3) // (IEEE-mandated square roots) // or p2=0 (other conditions) where sf (the status field completer) can have the same values as those given previously (Section 8.4.1) for arithmetic operations. If the qualifying predicate of the frsqrta instruction is zero, then predicate register p2 is cleared to zero and register f1 is left unchanged. If the source register contains NaTVal, then register f1 is set to NaTVal and predicate register p2 is cleared to zero. The frsqrta instruction uses the (biased) sign bit in the exponent field and leading bits <62:56> from the significand in register f3 as the index into a 256-entry lookup table. The significand in destination register f1 is given the value 1 in bit <63>, the 10-bit result in bits <62:53>, and 0 in bits <52:0>. The exponent is determined appropriately from the exponent field in the f3 source. The result is positive. This approximation has a known accuracy of at least 8.831 valid bits when compared to the mathematically precise reciprocal square root. Let us see how the frsqrta instruction can be used for computing a refined result (following Markstein). Suppose that y0 is the looked-up approximation to the exact reciprocal square root of some value b, and thus the relative error of approximating b 1/2 by y0 is
For convenience, define a quantity e0 that can be more easily computed:
Now the definition of e0 can be rearranged to provide improved approximations to b 1/2:
Finally, taking the square root of both sides and performing a series expansion yields
As e0 Similar strategies can also be derived for computing a refined square root. The base-level approximation is just by0. See Markstein for details about the refinement and the pitfalls that must be avoided to assure correctly rounded results using Itanium floating-point arithmetic instructions. 8.8.3 Floating-Point DivisionMarkstein very carefully outlines algorithms that use the Itanium instruction set to compute accurate reciprocals, quotients, remainders, square roots, and other functions in ways that adhere to IEEE conventions for rounding and reporting of special circumstances. Software support for floating-point division can be as varied as the languages available for a programming environment. High-level languages provide an option to view the assembly language that they generate; the -S option for Itanium C compilers reveals how differently each accomplishes division:
None of these routines has a publicly documented interface. 8.8.4 Open-Source Routines from Intel CorporationSection 7.7.2 introduced open-source routines from Intel Corporation that compute integer quotients and remainders. Analogous floating-point routines support different data sizes and a choice in performance between minimum latency for single calculations or maximum sustained throughput for repeated calculations, such as in a loop. The naming convention of the source files of each variant is easily discerned: [sgl,dbl,dbl_ext]_div_[min_lat,max_thr].s [sgl,dbl,dbl_ext]_sqrt_[min_lat,max_thr].s Entry point names with a br.call instruction are the name of the source file, without .s (e.g., dbl_div_min_lat for a double-precision floating-point division operation optimized for minimum latency in a single use). These routines may use numerous general and floating-point scratch registers as explained in Appendix D. For division, the calling routine should place the dividend onto the register stack as out0, the divisor as out1, and an address pointer for the returned quotient as out2. For square root, the calling routine should place the argument on the register stack as out0 and an address pointer for the returned result as out1. |
EAN: N/A
Pages: 223
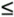 2 8.886 < 1.
2 8.886 < 1.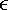
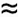 2
2