Computing Moving Averages
Problem
You'd like to smooth a set of time series data by computing moving averages.
Solution
You can compute moving averages in several ways in Excel. You can use the built-in Moving Average trendline charting feature, the Analysis ToolPak Moving Average feature, or spreadsheet functions to compute moving averages.
Discussion
Excel allows you to compute moving averages in several ways. I'll show you three ways: using chart trendlines, using the Analysis ToolPak, and using spreadsheet formulas.
Moving Average trendline
As mentioned in Recipe 6.2, you can add a trendline to a chart by selecting the data series and then right-clicking to reveal a pop-up menu. You can then select Add Trendline to open the Add Trendline dialog box shown in Figure 6-4.
Figure 6-4. Add Trendline dialog box
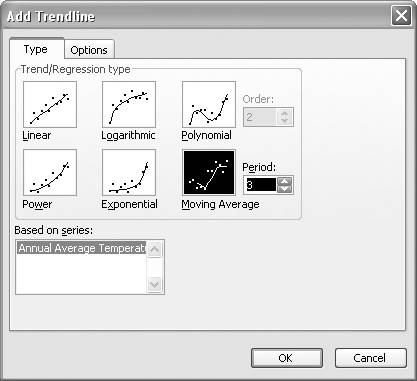
You can select from six different types of trendlines. In this case, select the Moving Average type. To the right of the Moving Average icon, you should see a Period spinner control (as shown in the figure). Use the spinner arrows to select the period over which averages will be computed. You can also type in a number. In this example, I entered 3 so as to create a three-year moving average trendline.
On the Options tab you can type in a name for the new trendline. Figure 6-5 shows the Options tab.
Figure 6-5. Add Trendline: Options tab

Moving Average trendlines have available only the "Trendline name" options. The other options apply to the other trendline types shown in Figure 6-4. (See Chapter 8 for examples using the other trendline types.)
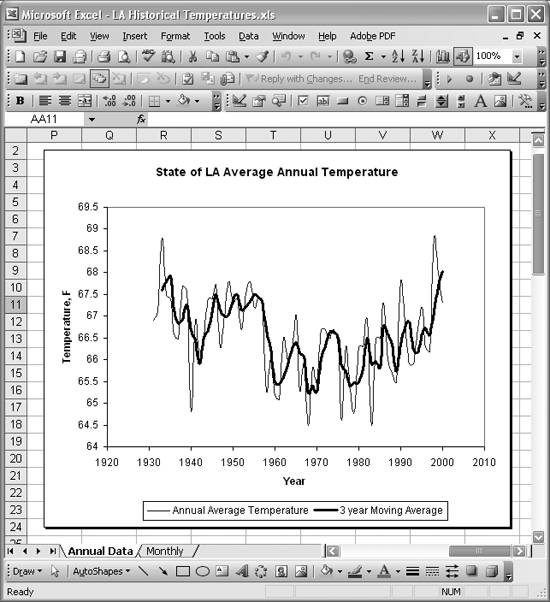
Pressing OK closes the Add Trendline dialog box and adds the new trendline to your chart. Figure 6-6 shows the time series from Figure 6-2 and Figure 6-3 with a three-year moving average trendline.
Figure 6-6. Three-year moving average trendline
If you decide to modify the resulting moving average trendline, perhaps changing the averaging period, simply select the trendline on the chart and then right-click to reveal a pop-up menu. Next, select Format Trendline from the pop-up menu to open the Format Trendline dialog box.
|
The Format Trendline dialog box includes the same the Add Trendline dialog box, where you can change the trendline type and any of its options. Further, the Format Trendline dialog box has an additional tab called Patterns that allows you to format the actual line drawn for the trendline. For example, you can change the line weight, color, and style.
Chart trendlines offer an easy way of creating moving average trendlines for time series data. However, this method does not allow you to extract the actual numerical values representing the moving average trendline. Also, this method requires that you first create a chart of your data. If you need numerical values for the trendline or you don't want to create a chart, then you can use one of the two following approaches.
Analysis ToolPak Moving Average
The Analysis ToolPak includes a Moving Average feature that allows you to compute moving averages in a manner similar to that of the Excel chart Moving Average trendline. The benefit of using the Analysis ToolPak is that you get the actual numerical data for the moving average series and not just a chart of the data.
To compute moving averages for a data series, select Tools  Data Analysis... from the main menu bar to open the Data Analysis dialog box. Figure 6-7 shows the Data Analysis dialog box, where youre presented with a list of analysis tools to choose from.
Data Analysis... from the main menu bar to open the Data Analysis dialog box. Figure 6-7 shows the Data Analysis dialog box, where youre presented with a list of analysis tools to choose from.
Figure 6-7. Data Analysis dialog box
Select Moving Average from this list and press OK to open the Moving Average dialog box shown in Figure 6-8.
Figure 6-8. Moving Average dialog box
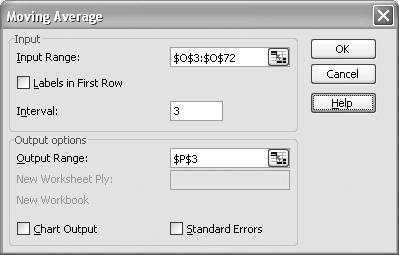
In the Input Range field, enter (or select directly on your spreadsheet) the cell range containing the y values of the data series for which you'd like to compute moving averages. For my example, cells O3 to O72 contained the relevant data.
Next, enter the Interval over which you'd like to compute averages. This is the same as the Period field used in the Trendline dialog box, as discussed earlier.
Finally, enter the topmost cell in the range where you'd like the output created. In this case I selected cell P3, to place the moving average data adjacent to the original time series data.
You may also elect to have a chart created automatically or have standard errors computed. Press OK to close the Moving Average dialog box and create the data. Your spreadsheet will now contain the new moving average data. Figure 6-9 shows a portion of the average annual temperature data series shown in Figure 6-6, along with the computed moving averages.
Figure 6-9. Moving Average results

Notice that the first two entries in the moving average series are #N/A. This is because the Moving Average tool computes moving averages based on the previous data points, and there are not enough points to compute the three-year average at the beginning of the series.
In Figure 6-9, I intentionally selected one of the computed moving averages to show you that these results are not static numerical values. Instead, the Moving Average tool entered formulas to compute the moving average. The formula used is the standard AVERAGE spreadsheet formula, as shown in the formula bar in Figure 6-9. Using the spreadsheet formula in this way means that if your original data changes, the moving average will update accordingly.
At this point, you can perform other spreadsheet operations on the moving average data or plot the data as you wish. This approach gives you greater flexibility, as opposed to the trendline moving average method discussed earlier. However, what if you want to compute the moving averages over a period centered about each data point in the original series? You can use spreadsheet formulas to accomplish this, as discussed in the next section.
Spreadsheet formulas
Aside from the two previous approaches, you can always use simple spreadsheet formulas to compute moving averages. Specifically, you can use the AVERAGE formula, as shown in Figure 6-10.
Figure 6-10. Centered moving averages

Figure 6-10 shows the same original data and three-year moving average data computed using the Analysis Toolpak from the previous section. Further, Figure 6-10 shows a new column of three-year moving averages computed using the AVERAGE formula manually. To generate the new column, I entered the AVERAGE formula in Q4 with the cell range O3:O5 passed as the argument. The formula is =AVERAGE(O3:O5). This formula computes the average of the three original series data points centered over the second data point. Once I had that formula entered, I simply copied and pasted the same formula in all the remaining cells in column Q, corresponding to the original data. Using relative cell references meant that Excel automatically adjusted the cell range argument passed into the AVERAGE formula. For example, Figure 6-10 shows the resulting formula contained in cell Q6, along with the corresponding cell range argument.
The result of these simple steps yields a new data series containing three-year centered moving averages. This approach is direct in that you don't need to use charts first if you don't want to, nor do you need to use the Analysis ToolPak. Further, this approach is flexible. For example, you can change the cell range passed into the AVERAGE formula to compute averages over any period of your choosing.
See Also
You can also compute weighted moving averages in Excel. See Recipe 6.4 to learn how.
Using Excel
- Introduction
- Navigating the Interface
- Entering Data
- Setting Cell Data Types
- Selecting More Than a Single Cell
- Entering Formulas
- Exploring the R1C1 Cell Reference Style
- Referring to More Than a Single Cell
- Understanding Operator Precedence
- Using Exponents in Formulas
- Exploring Functions
- Formatting Your Spreadsheets
- Defining Custom Format Styles
- Leveraging Copy, Cut, Paste, and Paste Special
- Using Cell Names (Like Programming Variables)
- Validating Data
- Taking Advantage of Macros
- Adding Comments and Equation Notes
- Getting Help
Getting Acquainted with Visual Basic for Applications
- Introduction
- Navigating the VBA Editor
- Writing Functions and Subroutines
- Working with Data Types
- Defining Variables
- Defining Constants
- Using Arrays
- Commenting Code
- Spanning Long Statements over Multiple Lines
- Using Conditional Statements
- Using Loops
- Debugging VBA Code
- Exploring VBAs Built-in Functions
- Exploring Excel Objects
- Creating Your Own Objects in VBA
- VBA Help
Collecting and Cleaning Up Data
- Introduction
- Importing Data from Text Files
- Importing Data from Delimited Text Files
- Importing Data Using Drag-and-Drop
- Importing Data from Access Databases
- Importing Data from Web Pages
- Parsing Data
- Removing Weird Characters from Imported Text
- Converting Units
- Sorting Data
- Filtering Data
- Looking Up Values in Tables
- Retrieving Data from XML Files
Charting
- Introduction
- Creating Simple Charts
- Exploring Chart Styles
- Formatting Charts
- Customizing Chart Axes
- Setting Log or Semilog Scales
- Using Multiple Axes
- Changing the Type of an Existing Chart
- Combining Chart Types
- Building 3D Surface Plots
- Preparing Contour Plots
- Annotating Charts
- Saving Custom Chart Types
- Copying Charts to Word
- Recipe 4-14. Displaying Error Bars
Statistical Analysis
- Introduction
- Computing Summary Statistics
- Plotting Frequency Distributions
- Calculating Confidence Intervals
- Correlating Data
- Ranking and Percentiles
- Performing Statistical Tests
- Conducting ANOVA
- Generating Random Numbers
- Sampling Data
Time Series Analysis
- Introduction
- Plotting Time Series Data
- Adding Trendlines
- Computing Moving Averages
- Smoothing Data Using Weighted Averages
- Centering Data
- Detrending a Time Series
- Estimating Seasonal Indices
- Deseasonalization of a Time Series
- Forecasting
- Applying Discrete Fourier Transforms
Mathematical Functions
- Introduction
- Using Summation Functions
- Delving into Division
- Mastering Multiplication
- Exploring Exponential and Logarithmic Functions
- Using Trigonometry Functions
- Seeing Signs
- Getting to the Root of Things
- Rounding and Truncating Numbers
- Converting Between Number Systems
- Manipulating Matrices
- Building Support for Vectors
- Using Spreadsheet Functions in VBA Code
- Dealing with Complex Numbers
Curve Fitting and Regression
- Introduction
- Performing Linear Curve Fitting Using Excel Charts
- Constructing Your Own Linear Fit Using Spreadsheet Functions
- Using a Single Spreadsheet Function for Linear Curve Fitting
- Performing Multiple Linear Regression
- Generating Nonlinear Curve Fits Using Excel Charts
- Fitting Nonlinear Curves Using Solver
- Assessing Goodness of Fit
- Computing Confidence Intervals
Solving Equations
- Introduction
- Finding Roots Graphically
- Solving Nonlinear Equations Iteratively
- Automating Tedious Problems with VBA
- Solving Linear Systems
- Tackling Nonlinear Systems of Equations
- Using Classical Methods for Solving Equations
Numerical Integration and Differentiation
- Introduction
- Integrating a Definite Integral
- Implementing the Trapezoidal Rule in VBA
- Computing the Center of an Area Using Numerical Integration
- Calculating the Second Moment of an Area
- Dealing with Double Integrals
- Numerical Differentiation
Solving Ordinary Differential Equations
- Introduction
- Solving First-Order Initial Value Problems
- Applying the Runge-Kutta Method to Second-Order Initial Value Problems
- Tackling Coupled Equations
- Shooting Boundary Value Problems
Solving Partial Differential Equations
- Introduction
- Leveraging Excel to Directly Solve Finite Difference Equations
- Recruiting Solver to Iteratively Solve Finite Difference Equations
- Solving Initial Value Problems
- Using Excel to Help Solve Problems Formulated Using the Finite Element Method
Performing Optimization Analyses in Excel
- Introduction
- Using Excel for Traditional Linear Programming
- Exploring Resource Allocation Optimization Problems
- Getting More Realistic Results with Integer Constraints
- Tackling Troublesome Problems
- Optimizing Engineering Design Problems
- Understanding Solver Reports
- Programming a Genetic Algorithm for Optimization
Introduction to Financial Calculations
- Introduction
- Computing Present Value
- Calculating Future Value
- Figuring Out Required Rate of Return
- Doubling Your Money
- Determining Monthly Payments
- Considering Cash Flow Alternatives
- Achieving a Certain Future Value
- Assessing Net Present Worth
- Estimating Rate of Return
- Solving Inverse Problems
- Figuring a Break-Even Point
Index
EAN: 2147483647
Pages: 206

