THE DATA CUBE OPERATOR CUBE

CUBE as proposed in Gray et al. (1997) generalizes SQL's GROUP BY operator. It computes the results of grouping a data set by all subsets of the specified d dimensions. Hence 2^d related groups are generated. We refer to each of these groups as a cuboid and to the overall result of CUBE as Cube. Figure 13 shows an example for a Cube for aggregate operator SUM that is computed for the dimensions time (T), product (P), and location (L), and measure attribute amount (A). The tables list all non-empty cells of the cuboids. In relational database terminology the cuboids are views generated by the corresponding GROUP BY queries as indicated in the figure. For simplicity we will use the dimension letters to refer to the cuboids; e.g., <TP> refers to the cuboid which is the result of grouping by time and product. Cuboid <TPL>, which has the most detailed information, is referred to as the base cuboid.

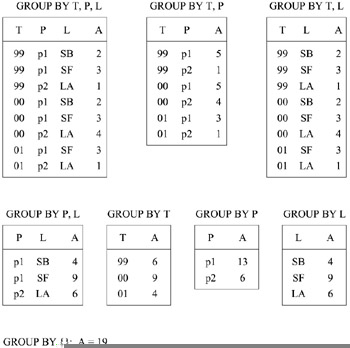
Figure 13: Cuboids of a Three-Dimensional Example Cube

Cube's main purpose is to support aggregate queries. A query that only selects on a few attributes can be efficiently answered by processing the appropriate compact cuboid. For instance, finding the total sales volume in 1999 only costs a lookup on <T>, while computing the same result on the base cuboid would require finding and aggregating multiple tuples. Specialized index structures for Cube, e.g., Johnson & Shasha (1997, 1999) and Roussopoulos, Kotidis, & Roussopoulos (1997), further reduce query time.

Note however, that Cube pays for this query support with a possibly large amount of redundancy. Each aggregate query that could be answered by a certain cuboid C could also be answered by the base cuboid (or any other cuboid whose set of group-by attributes contains C's group-by attributes). For sparse high-dimensional data sets, materializing all views will lead to database explosion (cf., Pendse & Creeth, 2001). This is caused by the large number of cuboids (2^d) and the possibility that a cuboid does not perform a considerable amount of aggregation. We can already observe this effect in our (fairly dense) example in Figure 13. Cuboids <TPL> and <TL> contain the same number of tuples, i.e., the aggregation of <TPL> along the product dimension does not result in any aggregation. Higher dimensionality and greater sparseness tend to amplify the space explosion effect. At the same time the redundancy between the cuboids also increases update costs.

After Cube was proposed, most research focused on its efficient computation and space reduction. Bayer and Ramakrishnan (1999) propose a technique that restricts the generation of cuboids or partitions of cuboids to those that achieve "enough" aggregation. Other researchers (e.g., Gupta et al., 1997; Harinarayan, Rajaraman, & Ullman, 1996; Shukla, Deshpande, & Naughton, 2000; Smith et al., 1998) formulated the computation of Cube as an optimization problem. Their goal is to select and materialize only a subset of the cuboids (and indexes in case of Gupta et al., 1997) in order to minimize the query cost subject to storage constraints. Later work stressed the importance of also addressing Cube maintenance issues. Consequently the approaches in Baralis, Paraboschi, & Teniente (1997), Gupta (1997), and Gupta & Mumick (1999) extend the earlier work by explicitly taking update costs into account for the optimization problem.

Interestingly, the multidimensional data cube model provides a more compact description of the Cube by conceptually combining all 2^d cuboids into a single hyper-rectangle. Each dimension is augmented by the additional value "ALL," which represents the aggregation over the complete dimension. The additional surface layers for ALL coordinates are "padded" to the base cuboid and store the corresponding cuboids. Figure 14 illustrates this for the example from Figure 13.

Figure 14: Cube as a Multidimensional Data Cube; Cuboids of Figure 13 Indicated