53. t-Test2-Sample Overview The 2-Sample t-Test is used to compare two sample means against each other. For example, a Team might need to determine if two operators are taking the same amount of time to perform a task. A data sample would be taken of, for example, 25 points for each operator to make the judgment, and the result is the likelihood that both operators' average task time (as work continues) is the same. Thus, a sample of data points (lower curves) is taken from the two processes (the populations of all data points, upper curves), as shown in Figure 7.53.1. From the characteristics of the samples (mean  standard deviation s, and sample size n), an inference is made on the location of the population means μ relative to the each other. The result would be a degree of confidence (a p-value) that the samples come from populations with the same mean. standard deviation s, and sample size n), an inference is made on the location of the population means μ relative to the each other. The result would be a degree of confidence (a p-value) that the samples come from populations with the same mean. Figure 7.53.1. Graphical representation of a 2-Sample t-Test. 
Caution: It should be noted that there is a subtly different test known as a Paired t-Test that is often confused with a 2-Sample t-Test. A 2-Sample t-Test for the preceding example looks at the mean of the sample for Operator 1 versus the mean of the sample for Operator 2. The Paired t-Test, on the other hand, is used to compare two samples against each other, but where a data point from each set needs to be considered together in pairs. For example, a Team might need to determine if two operators are quoting the same price for packages of products or services. It makes no sense to compare the average of all the quotes for Operator 1 to the average of all the quotes for Operator 2. Each package quote needs to be examined separately, making paired comparisons of Operator 1's quote for the package and Operator 2's quote for the package. In this case refer to "t-TestPaired" in this chapter. Roadmap The roadmap of the test analysis itself is shown graphically in Figure 7.53.2. Figure 7.53.2. 2-Sample t-Test Roadmap[92] 
[92] Roadmap adapted from SBTI's Process Improvement Methodology training material.
Step 1. | Identify the metric and levels to be examined (two operators or such like). Analysis of this kind should be done in the Analyze Phase at the earliest, so the metric should be well defined and understood at this point (see "KPOVs and Data" in this chapter).
| | | Step 2. | Determine the sample size. This can be as simple as taking the suggested 25 data points or using a sample size calculator in a statistical package. These rely on an equation relating the sample size to the following:
The standard deviations (the spread of the data) of each population. This would have to be approximated from historical data. The required power of the test (the likelihood of the test identifying a difference between the means if there truly was one). This is usually set at 0.8 or 80%. The power is actually (1 β), where β is the likelihood of giving a false negative, and might need to be entered in the software as a β of 0.2 or 20%. The size of the difference σ between the means that is desired to be detected (i.e., the distance between the means that would lead the Team to say that the two values were different). The alpha level for the test (the likelihood of the test giving a false positive) usually set at 0.05 or 5% and represents the cutoff for the p-value (remember if p is low, H0 must go). Whether the test is one-tailed or two-tailed see "Other Options" in this section.
| Step 3. | Collect two sample data sets, one from each population (process), following the rules of good experimentation.
| Step 4. | Examine stability of both sample data sets using a Control Chart for each, typically an Individuals and Moving Range Chart (I-MR). A Control Chart identifies whether the processes are stable, having
This is important because if the processes are moving around, it is impossible to sensibly make the call as to whether they are the same or not.
| | | Step 5. | Examine normality of the sample data sets using a Normality Test for each. This is important because the statistical tests in Step 6 and 7 rely on it, but in simple terms if the sample curves in Figure 7.53.1 were strange shapes it would be difficult to determine if the middles were aligned. In fact if data becomes skewed, then the mean is probably not the best measure of center (a t-Test is a mean-based test), and a median-based test is probably better. The longer tail on the right of the example curve in Figure 7.53.3 drags the mean to the right, however, the median tends to remain constant. Medians-based tests could in theory be used for everything as a more robust test, but they are less powerful than their means-based counterparts and hence the desire to go with the mean.
Figure 7.53.3. Measures of Center. 
| Step 6. | Perform a Test of Equal Variance on the sample data sets. In simple terms, any test of centering (Step 7) looks to measure the distance from μ1 to μ2 in units of standard deviation. Figure 7.53.4 highlights the problem that if the variances of each population were different, then measuring the difference between them in units of standard deviation would be different using σ1 versus σ2. If the standard deviations are different, then the test should use a composite value known as the pooled standard deviation.
Figure 7.53.4. The impact of different variances. 
The Test of Equal Variance uses the sample data sets and has hypotheses:
| | | Step 7. | Perform the 2-Sample t-Test if both of the sample data sets were determined to be normal in Step 5. The hypotheses in this case are
The output of Step 6 also needs to be included in the test. Most statistical software packages include a checkbox or similar to select if the variances are equal or not.
If the data in either or both of the samples were non-normal, then as per Figure 7.53.2:
Continue unabated with the 2-Sample t-Test if the sample size is large enough (>25) Transform the data first and then perform the analysis using the 2-Sample t-Test[93] [93] Transformation of data is considered beyond the scope of this book.
Perform the median-based equivalent test, a Mann-Whitney Test
The last option often worries Belts, but the medians tests look identical in form to the means test and both return the key item, a p-value (the p-values for a means test and a medians test on the same data are unlikely to be the same though).
|
Interpreting the Output The 2-Sample t-Test[94] compares the sample characteristics (mean standard deviation s, and sample size n) to a reference distribution, the t-distribution, to determine whether the sample data sets indicate that the populations are statistically different or not. Amongst other things it returns a p-value, the likelihood that for the sample a difference between means this large could have occurred purely by random chance even if the populations were aligned. [94] The technical details of a t-Test are covered in most statistics textbooks; Statistics for Management and Economics by Keller and Warrack makes it understandable to non-statisticians.
Based on the t-Test and the p-values, statements can be generally formed as follows: Based on the data, I can say that there is a difference and there is a (p-value) chance that I am wrong Or based on the data, I can say that there is an important effect and there is a (p-value) chance the result is just due to chance
Output from a 2-Sample t-Test is shown in Figure 7.53.5. Figure 7.53.5. Test results for a comparison of sample of Bob's versus Jane's performance (output from Minitab v14).Two-Sample T-Test and CI: Bob, Jane | | | Two-Sample T for Bob vs Jane | | | | | N | Mean | St Dev | SE Mean | | | Bob | 100 | 24.811 | 0.973 | 0.097 | | | Jane | 100 | 25.525 | 0.904 | 0.090 | | | Difference = mu (Bob) mu (Jane) | | | Estimate for difference: 0.714000 | | | 95% CI for difference: ( 0.975938, 0.452062) | | | T Test of difference = 0 (vs not =): T-Value = 5.38 | P-Value = 0.000 | DF = 196 |
From the example results A sample of 100 data points was taken for each operator Bob's sample mean was 24.811, Jane's was 25.525 Bob's sample standard deviation was 0.973, Jane's was 0.904 The test is based on the hypotheses:μBob μJane = 0 (H0) versus μBob μJane  0 (Ha) 0 (Ha)
There is a 95% likelihood that the difference between the population means lies between 0.975938 and 0.452062 The means of the samples are 5.38 Standard Errors apart (the t-value) The likelihood of seeing sample means 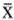 this far apart (if the populations were perfectly aligned) is 0.0% (p-value), which is below 0.05; thus, the conclusion is that Bobs is performing significantly differently from Jane given the sample data. this far apart (if the populations were perfectly aligned) is 0.0% (p-value), which is below 0.05; thus, the conclusion is that Bobs is performing significantly differently from Jane given the sample data.
Other Options The preceding test with the hypotheses defined as The test is known as a two-tailed test, because (by the " " in Ha) it is not known whether the mean of population 1 is above or below the mean of population 2, and, hence, the test needs to cover both sides (tails). " in Ha) it is not known whether the mean of population 1 is above or below the mean of population 2, and, hence, the test needs to cover both sides (tails). A one-tailed test on the other hand is used when it can be stated up front whether the mean of population 1 is above or below the mean of population 2. The hypotheses in this case is either: H0: Population (process) μ1 = μ2 Ha: Population (process) μ1 > μ2 or H0: Population (process) μ1 = μ2 Ha: Population (process) μ1 < μ2. A one-tailed test (greater than or less than) can detect a smaller difference between the means than a two-tailed test[95]. Given the choice, go with the one-tailed test if there is data to show which of the two population means is greater. [95] An explanation for this can be found in most statistical textbooks; Statistics for Management and Economics by Keller and Warrack is useful in this case.
|

 standard deviation s, and sample size n), an inference is made on the location of the population means μ relative to the each other. The result would be a degree of confidence (a p-value) that the samples come from populations with the same mean.
standard deviation s, and sample size n), an inference is made on the location of the population means μ relative to the each other. The result would be a degree of confidence (a p-value) that the samples come from populations with the same mean.


 22 (variances not equal)
22 (variances not equal)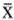 this far apart (if the populations were perfectly aligned) is 0.0% (p-value), which is below 0.05; thus, the conclusion is that Bobs is performing significantly differently from Jane given the sample data.
this far apart (if the populations were perfectly aligned) is 0.0% (p-value), which is below 0.05; thus, the conclusion is that Bobs is performing significantly differently from Jane given the sample data.