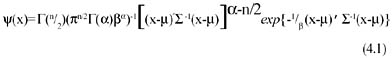|  |  | | | Chapter X - Maximum Performance Efficiency Approaches for Estimating Best Practice Costs | | Data Mining: Opportunities and Challenges | | by John Wang (ed) | | | Idea Group Publishing 2003 | | | | Brought to you by Team-Fly | | | A basic assumption underlying the MPE estimation principle's applicability is that the sample of units under analysis does, in fact, have the goal of achieving maximum (1.0) efficiency. This is a model aptness issue that parallels the requirement of N(0,σ2) residuals in OLS regression theory. In the present MPE case, the corresponding issue is to specify a measured characteristic of the vj that indicates consistency with a goal or target of unity (1.0) efficiency. In this section, we propose what may be called the normal-like-or-better effectiveness criterion for these fitted efficiency scores. As a model for appropriate concentration on a target, we begin with an interpretation of the multivariate normal distribution, N (μ,Σ), on  . If a distribution of attempts has the N(μ,Σ) or even higher concentration of density at the mode μ, then we propose this as evidence that μ is indeed a plausible target of the attempts. This is exemplified by considering a distribution model for the results of throwing darts at a bull's-eye target. Common experience suggests that a bivariate normal density represents such data reasonably well. Steeper or flatter densities would still be indicative of effective attempts, but densities whose modes do not coincide with the target would cause doubts about whether the attempts have been effective or whether another target better explains the data. We call this normal-like-orbetter (NLOB) performance effectiveness. It is next necessary to obtain the analog of this criterion for the efficiency performance data Yrj relevant to the present context. . If a distribution of attempts has the N(μ,Σ) or even higher concentration of density at the mode μ, then we propose this as evidence that μ is indeed a plausible target of the attempts. This is exemplified by considering a distribution model for the results of throwing darts at a bull's-eye target. Common experience suggests that a bivariate normal density represents such data reasonably well. Steeper or flatter densities would still be indicative of effective attempts, but densities whose modes do not coincide with the target would cause doubts about whether the attempts have been effective or whether another target better explains the data. We call this normal-like-orbetter (NLOB) performance effectiveness. It is next necessary to obtain the analog of this criterion for the efficiency performance data Yrj relevant to the present context. If x is distributed as N (μ,Σ) on  , then it well known that the quadratic form, w(x) = (x−μ)′Σ−1(x−μ) is gamma(α,β), where α = n/2 and β =2. This distribution is also called the Chisquare distribution with n degrees of freedom (see Law & Kelton, 1982). We may note that for this case w(x) is in the nature of a squared distance from the target set {μ}. It is useful to derive this result by a different technique. Vertical density representation (VDR) is a technique for representing a multivariate density by way of a univariate density called the ordinate or vertical density, and uniform distributions over the equidensity contours of the original multivariate density. VDR was introduced in Troutt (1993). (See also Kotz, Fang & Liang, 1997; Kotz & Troutt, 1996; Troutt,1991; and Troutt & Pang, 1996.) The version of VDR needed for the present purpose can be derived as follows. Let w(x) be a continuous convex function on , then it well known that the quadratic form, w(x) = (x−μ)′Σ−1(x−μ) is gamma(α,β), where α = n/2 and β =2. This distribution is also called the Chisquare distribution with n degrees of freedom (see Law & Kelton, 1982). We may note that for this case w(x) is in the nature of a squared distance from the target set {μ}. It is useful to derive this result by a different technique. Vertical density representation (VDR) is a technique for representing a multivariate density by way of a univariate density called the ordinate or vertical density, and uniform distributions over the equidensity contours of the original multivariate density. VDR was introduced in Troutt (1993). (See also Kotz, Fang & Liang, 1997; Kotz & Troutt, 1996; Troutt,1991; and Troutt & Pang, 1996.) The version of VDR needed for the present purpose can be derived as follows. Let w(x) be a continuous convex function on  with range [0,∞); and let g(w) be a density on [0,∞). Suppose that for each value of u≥0, x is uniformly distributed on the set {x:w(x) =u}. Consider the process of sampling a value of u according to the g(w) density, and then sampling a vector, x, according to the uniform distribution on the set {x:w(x) =u}. Next let f(x) be the density of the resulting x variates on with range [0,∞); and let g(w) be a density on [0,∞). Suppose that for each value of u≥0, x is uniformly distributed on the set {x:w(x) =u}. Consider the process of sampling a value of u according to the g(w) density, and then sampling a vector, x, according to the uniform distribution on the set {x:w(x) =u}. Next let f(x) be the density of the resulting x variates on 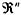 . Finally, let A(u) be the volume (Lebesgue measure) of the set {x : w(x) ≤ u}. Then we have the following VDR theorem that relates g(w) and f(x) in . Finally, let A(u) be the volume (Lebesgue measure) of the set {x : w(x) ≤ u}. Then we have the following VDR theorem that relates g(w) and f(x) in  . The proof is given in the Appendix. . The proof is given in the Appendix. Theorem 2: If A(u) is differentiable on [0,∞) with A'(u) strictly positive, then x is distributed according to the density f(x) where 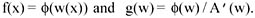
Theorem 2 can be applied to derive a very general density class for performance related to squared distance type error measures. The set {x: (x−μ)′ Σ−1 (x−μ) ≤ u} has volume, A(u), given by A(u) = αn |Σ|1/2 un/2 where αn = πn/2 / n/2 Γ(n/2), (Fleming, 1977), so that A/(u) = n/2 αn |Σ|1/2 un/2−1. The gamma(α,β) density is given by 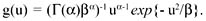
Therefore Theorem 2 implies that if w(x) = (x−μ)/Σ−1(x−μ) and g(u) = gamma (α,β), then the corresponding f(x), which we now rename as ψ (x) = ψ (x;n,a,β), is given by 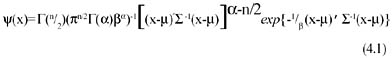
For this density class we have the following observations: -
If α = n/2 and β =2, then ψ(x) is the multivariate normal density, N(μ,Σ). -
If α = n/2 and β ≠ 2, then ψ(x) is steeper or flatter than N(μ,Σ) according to whether β < 2 or β>2, respectively. We call these densities the normal-like densities. -
If α < n/2, then ψ(x) is unbounded at its mode, μ, but may be more or less steep according to the value of β. We call this class the better-than-normal-like density class. -
If α > n/2, then ψ(x) has zero density at the target, μ, and low values throughout neighborhoods of μ. This suggests that attempts at the target are not effective. The data may have arisen in pursuit of a different target or simply not be effective for any target. For densities in Category (3), the unbounded mode concentrates more probability near the target and suggests a higher level of expertise than that evidenced by the finite-at-mode N(μ,Σ) class. It seems reasonable to refer to α in this context as the expertise, mode, or target effectiveness parameter, while β is a scale or precision parameter. Thus, if α ≤ n/2, we call ψ(x) the normal-like-or-better performance density. To summarize, if attempts at a target set in 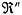 have a basic squared distance error measure and this measure is distributed with the gamma(α,β) density with α ≤ n/2, then the performance with respect to this target set is normal - like-or-better (NLOB). have a basic squared distance error measure and this measure is distributed with the gamma(α,β) density with α ≤ n/2, then the performance with respect to this target set is normal - like-or-better (NLOB). We extend this target effectiveness criterion to the present context as follows. The target set is  . If ΣarYrj = vj, then the distance of Yrj from the target set is (1−v) Q%aQ%−1. Since 0 ≤ v ≤ 1, we employ the transformation w =(−ln v)2 = (ln v)2. This transformation has the properties that w ≅ (1−v)2 near v =1 and wε[0,∞). Therefore, w/Q%aQ%2 = (ln v)2/Q%aQ%2 is an approximate squared distance measure near the target set. Since the Q%aQ%2 term is a scale factor, it can be absorbed into the β parameter of gamma(α,β). We therefore consider the NLOB effectiveness criterion to hold if w has the gamma(α,β) density with α ≤ 4/2 =2. That is, such performance is analogous to that of unbiased normal - like-or-better distributed attempts at a target in . If ΣarYrj = vj, then the distance of Yrj from the target set is (1−v) Q%aQ%−1. Since 0 ≤ v ≤ 1, we employ the transformation w =(−ln v)2 = (ln v)2. This transformation has the properties that w ≅ (1−v)2 near v =1 and wε[0,∞). Therefore, w/Q%aQ%2 = (ln v)2/Q%aQ%2 is an approximate squared distance measure near the target set. Since the Q%aQ%2 term is a scale factor, it can be absorbed into the β parameter of gamma(α,β). We therefore consider the NLOB effectiveness criterion to hold if w has the gamma(α,β) density with α ≤ 4/2 =2. That is, such performance is analogous to that of unbiased normal - like-or-better distributed attempts at a target in 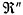 . There is one additional consideration before applying this effectiveness criterion to the present data. In the LP estimation model MPE, at least one efficiency, vj, must be unity (and hence wj = 0). This is because at least one constraint (2.6) must be active in an optimal solution of the MPE model. We therefore consider the model for the wj to be . There is one additional consideration before applying this effectiveness criterion to the present data. In the LP estimation model MPE, at least one efficiency, vj, must be unity (and hence wj = 0). This is because at least one constraint (2.6) must be active in an optimal solution of the MPE model. We therefore consider the model for the wj to be 
where p is the frequency of zero values (here p = 3/62 = 0.048 from Table 1), and δ(0) is the degenerate density concentrated at w = 0. We call this the gamma-plus-zero density, gamma(α,β)+0. For this data, we regard the NLOB criterion to hold if it holds for the gamma density in (4.2). When the gamma(α,β) density is fitted to the strictly positive w values, then NLOB requires that α ≤ 2. For the data of wj = (ln vj)2 based on Table 1, Column 7, the parameter value estimates obtained by the Method of Moments (see, for example, Bickell & Doksum, 1977) are α = 1.07 and β = 0.32. This method was chosen because the BESTFIT software experienced difficulty in convergence using its default Maximum Likelihood Estimation procedure. The Method of Moments estimates parameters by setting theoretical moments equal to sample moments. For the gamma(α,β) density, μ = αβ, and σ2 = αβ2. If 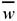 and s2 are the sample mean and variance of the positive wj values, then the α and β estimates are given by and s2 are the sample mean and variance of the positive wj values, then the α and β estimates are given by 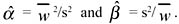
Tests of fit of the wj data to the gamma (α = 1.07, β = 0.32) density were carried out using the software BestFit (1995). All three tests provided in BestFit the Chi-square, Kolmogorov - Smirnov, and the Anderson-Darling indicated acceptance of the gamma model with confidence levels greater than 0.95. In addition, for each of these tests, the gamma model was judged best fitting (rank one) among the densities in the library of BestFit . We therefore conclude that the NLOB condition is met. Use of the NLOB criterion in this way may be regarded as somewhat stringent in that the zero data are only used to define the target and are not used to assess NLOB target effectiveness. The NLOB criterion is important in establishing whether the estimated cost model is a plausible goal of the units being studied. The MPE model will produce estimates for any arbitrary set of Yrj data. However, if the resulting vj data were, for example, uniformly distributed on [0,1], there would be little confidence in the estimated model. | | Brought to you by Team-Fly | | | |