3.11 The Circle

3.11 The Circle

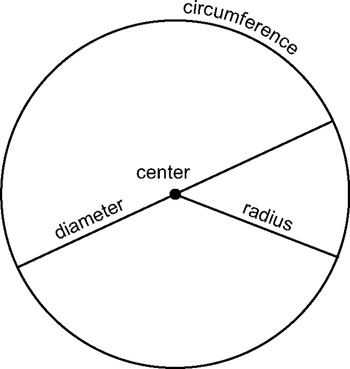
Figure 3.21: Circumference, diameter, and radius

The circle is a 2D shape with a center point bounded by a curved line, called the circumference. It stretches right around the center point in one complete revolution. From the center point to any point on the circumference, a straight line can be drawn and any one of these lines will be the same distance as the other. This line is called a radius. Similarly, a straight line can be drawn from any point on the circumference, through the center, to reach the opposite side of the circumference; naturally, this line is twice the length of the radius. This is called the diameter.

3.11.1 Chords

A chord is a straight line that touches the circumference twice and divides the circle into two segments. The segments are called the major segment (larger) and the minor segment (smaller). The diameter is considered to be the longest chord of a circle.

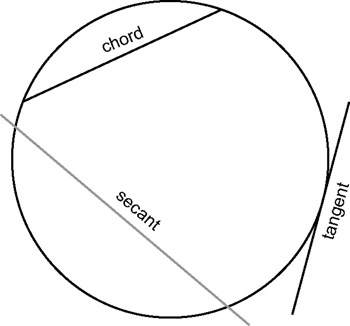
Figure 3.22

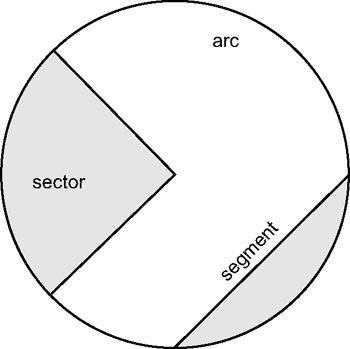
Figure 3.23

3.11.2 Central and Inscribed Angles

In a circle there are two kinds of angles, a central angle and an inscribed angle. A central angle has its vertex at the center of the circle, while an inscribed angle is formed by the vertex at the intersection of two or more chords anywhere in the circle.

3.11.3 Length of a Chord

A chord is said to subtend a central angle, meaning that a chord stretches under a central angle (an angle at the center). Given a diameter of a circle and a central angle defining the length of a chord, it is possible to calculate the ratio of the diameter to the chord. And, if the diameter is known, then the length of a chord can be established.

The ratio of the diameter to the chord is half the sine of the central angle.

3.11.4 Pi (π)

It has been demonstrated that to establish the ratio between two lines, the length of one should be divided by the length of the other. So, if the quotient is 2, one line is twice as long as the other, and the other is half as long. The circumference of a circle is a curved line stretching around the circle. This line can be unravelled and straightened out to make a straight line. If this line is compared to the diameter, such that you establish the ratio of the diameter to the circumference, the circumference will be found to be so many times greater than the diameter. This ratio is an endless number, but is generally approximated to 3.14, and is called the number Pi. So, the circumference is 3.14 times longer than the diameter, and this ratio is true for all circles.

So:

• π = C / D

Which means:

• C = πD

And since the diameter is two times the radius (D = 2r) then:

• C = π2r

3.11.5 Radians

In mathematics, an arc defines a segment of a circle; the curved line is a subsection of the circumference; and each straight line is said to be a radius of the circle. Until now, the unit of measure to express angles has been degrees. In the degree system, a right angle (one quarter turn) is 90 degrees, half a turn is 180 degrees, and one complete turn (revolution) is 360 degrees. However, there is another unit of measure for angles, and during the course of game programming it will inevitably be encountered. That unit of angle measure is called radians.

Radian measure is related to the circle. It is defined as the ratio between a radius and the length of an arc; so where the radius and length of an arc are equal, that is said to be 1 radian since their quotient will be 1 and therefore their ratio is 1:1. See Appendix B for a conversion chart from degrees to radians and vice versa.

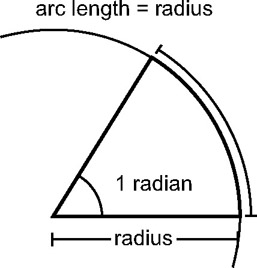
Figure 3.24: Radian

The ratio of the circumference to the diameter is π, and the ratio of the radius to the circumference is 2π. Thus, there are said to be 2π radii (plural for radius) on the circumference. For this reason, there are 2π radians in a complete revolution because that is how many times the radius can fit onto the circumference. There are π radians in a half turn, and π / 2 radians in a right angle.

Note 

You might have noticed that each right angle is an increase of π / 2. So: π / 2 = 90 degrees, π = 180 degrees, 2π = 360 degrees.