Tool 10: Analysis of Variance

AKA

AKA ANOVA, Hypothesis Testing (ANOVA), F-Test

Classification

Analyzing/Trending (AT)

Tool description

The analysis of variance is an inferential statistical technique designed to test for significance of the differences among two or more sample means. Some applications include the ability to make inferences about the population from which the samples were drawn, to identify differences or variations in statistical process control (SPC) analyses, and to provide for analysis and comparison of factorial designs in design of experiments (DOE).

Typical application

• To identify differences or variance in productivity, quality, methods, factorial designs, performance, and many other applications.

• To check for variation among sample or group means.

• To perform hypothesis testing on interval (quantitative) data sets.

Problem-solving phase

→	Select and define problem or opportunity
→	Identify and analyze causes or potential change
	Develop and plan possible solutions or change
→	Implement and evaluate solution or change
→	Measure and report solution or change results
	Recognize and reward team efforts

Typically used by

1	Research/statistics
	Creativity/innovation
2	Engineering
	Project management
	Manufacturing
	Marketing/sales
	Administration/documentation
	Servicing/support
	Customer/quality metrics
3	Change management

links to other tools

before

• Variance Analysis

• Standard Deviation

• Process Capability Ratios

• Normal Probability Destribution

• Descriptive Statistics

after

• Problem specification

• Work flow analysis (WFA)

• Prioritization matrix

• Process analysis

• Problem analysis

Notes and key points

• Definition: The analysis of variance (ANOVA) is a technique often applied in the field of inferential statistics to test whether the means of more than two quantative data sets of samples or populations differ.

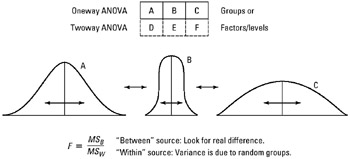
• Variance analysis:

  

  • Refer to the hypothesis testing procedure (see tool 92). The analysis of variance test is frequently used in testing hypotheses.

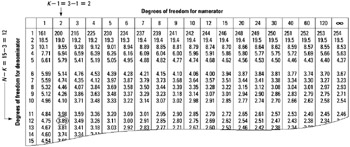
  • Partial analysis of variance (ANOVA) distribution table— critical values at the .05 level of significance. (Refer to the Appendix, Table C for complete ANOVA critical values table.)

F-Distribution: 05 One-Tail, 10 Two-Tail Test

Step-by-step procedure

• STEP 1 First, daily product defect rates are collected on three different methods of production. See example Three Production Methods and Their Daily Product Defect Rates.

• STEP 2 The Null Hypothesis (H₀) is stated: There is no statistically significant difference in the daily product defect rates and the production methods used measured at .05 alpha (level of sigificance) using a one tailed F-test (ANOVA).

• STEP 3 The eight-step hypothesis testing procedure is used to arrive at a decision (see Hypothesis Testing [CHI-square] for example).

• STEP 4 The calcultions are performed in this example.

  Note

  The analysis of variance calculations are time consuming and often difficult to calculate. Any basic software program on statistics will perform calculations and provide a printout similar to that shown in this example.

• STEP 5 Finally, the test result is verified against the critical value located in the ANOVA distribution table (notes and key points). On the basis of the test result F-ratio = 5.74 and the critical value = 3.89 (which is lower), the Null Hypothesis (H₀) is rejected. There is a statistically significant difference in the three production methods and their daily product defect rates.

Example of tool application

Three Production Methods and Their Daily Product Defect Rates

Three Production Methods and Their Daily Product Defect Rates (continued)