Using Mathematical and Financial Functions

There are more mathematical, financial, and statistical functions than could possibly be covered in one short section. For the most part, these functions use operands and operators to evaluate numeric data. This section doesn't attempt to completely cover each, but rather provides a succinct review of those most often used.

The Abs Function

The Abs function returns the absolute value of a numeric value. This function uses the form

 Abs(number) 

where number is any valid numeric expression or a literal numeric value. The returned value is the same as number, but without the sign. For instance, the function

 Abs(intValue) 

where intValue is an Integer variable that stores the value 3, returns the Integer value of 3.

The Int Function

The Int function returns the integer portion of a numeric value. This function takes the form

 Int(number) 

where number is required and can be any valid Numeric data type. The Int function does no rounding; it simply removes the fractional portion of number, if one exists. For instance, the function

 Int(10.9) 

returns 10, not 11. If number is negative, Int returns the first negative integer less than or equal to number. For instance, the function

 Int(-10.9) 

returns 11.

When converting values, consider using CInt instead of Int, but keep in mind that the two functions aren't entirely interchangeable. The Int function won't convert number's data type. Although CInt is often the better choice, it won't return the same results. Consider the task and use the most appropriate function.

The Rnd Function

Use the Rnd function to return a random number. This function's optional argument is any valid numeric expression. The function takes the form

 Rnd[(seed)] 

where seed determines the range of the returned random number as follows:

• When seed is less than 0, Rnd returns the same random number.

• When seed is greater than 0, Rnd returns the next number in the sequence of random values as determined internally.

• When seed equals 0, Rnd returns the most recently generated random number.

• When seed is omitted, Rnd returns the next number in the sequence of random values, as determined internally.

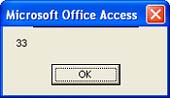
TIP

Sometimes you must work with values that don't generate random values as required. For instance, suppose you're working with values that are less than 0, but you don't want to generate the same value over and over. When this is the case, use the Randomize statement to reset the internal seed value so the Rnd function can return seemingly unique random values that don't repeat.

A Mathematical Function Example

The first example used the CDate function to convert a Variant data type to a valid Date data type. You might also remember that the result wasn't a whole number. You can display a whole number by adding an Int function to the equation. To do so:

1. Return to the Chapter5 module and find GetDate().
   
   

2. Comment out the MsgBox statement by selecting that statement and clicking the Comment Block tool on the Edit toolbar. Or, simply insert an apostrophe character (') at the beginning of the statement.
   
   

3. Enter the following new code
   
   

   
   

    MsgBox Int(Now - varDate) 

   
   

4. With the insertion point in the Sub procedure, press F5.
   
   

5. Enter 3/1/2004 in the input box and click OK. This time, the message box displays a whole number, as shown in Figure 5.9. Click OK to clear the message box.
   
   

   Figure 5.9. Adding the Int function improves your message's display.

   

   
   

The Ddb Function

The Ddb function returns a Double data type that represents the depreciation of an asset for a specific time period using the predefined double-declining balance method. This function takes the form

 Ddb(cost, salvage, life, period[, factor]) 

where cost is a Double value or expression that represents the asset's initial cost, and salvage is a Double value that specifies the asset's value at the end of life, which is a Double value that expresses the length of the asset's life. Likewise, period is a Double that expresses the period for which the depreciation is to be calculated. The optional factor argument is a Variant that determines the rate at which the asset balance declines. When omitted, the double-declining method is assumed (although documentation doesn't seem to support any other values).

The FV Function

When you need to calculate the future value of an annuity, use the Fv function. This function returns a Double value and uses the form

 Fv(rate, nper, pmt[, pv [, type]]) 

where rate is a Double value that specifies the interest rate per period, nper is an Integer value that specifies the number of payment periods in the annuity, and pmt is a Double value that specifies the payment made each period. The two optional arguments, pv and type, are Variant data types that represent the present value and whether payments are due at the start or the end of the period, respectively.

The IPmt Function

Calculate the interest payment for a given period of an annuity using the IPmt function. This function returns a Double and takes the form

 IPmt(rate, per, nper, pv[, fv[, type]]) 

where rate is a Double that states the period's interest rate, per is any numeric expression that specifies the period for which the payment is to be calculated, nper is a Double that represents the total number of payments, and pv is any valid numeric expression that specifies the present value. The two optional arguments, fv and type, are Variant data types that indicate the future value or cash balance after the final payment and whether the payments are due at the start or the end of the period.

The NPer Function

The Nper function calculates the number of periods for an annuity as a Double. Use the form

 NPer(rate, pmt, pv[, fv [, type]]) 

where rate is a Double that represents the interest rate per period, pmt is a Double that specifies the payment made each period, and pv is a Double that identifies the present value. The two optional arguments, fv and type, are Variant data types that identify the future value of the series of payments and whether the payments are due at the start or the end of the period.

The Pmt Function

Use the Pmt function to calculate the payment for an annuity as a Double. This function takes the form

 Pmt(rate, nper, pv[, fv[, type]]) 

where rate is a Double that represents the interest rate per period, nper is an Integer that specifies the total number of payments, and pv is a Double that identifies the present value. The two optional arguments, fv and type, are Variant data types that identify the future value of the series of payments and whether the payments are due at the start or the end of the period.

The PPmt Function

Use the PPmt function to calculate the principal payment for an annuity as a Double. This function takes the form

 PPmt(rate, per, nper, pv[, fv[, type]]) 

where rate is a Double that represents the interest rate per period, per is a Double that represents the period for which a payment is to be calculated, nper is a Double that specifies the total number of payments, and pv is a Double that identifies the present value. The two optional arguments, fv and type, are Variant data types that identify the future value and whether payments are due at the start or the end of the period.

The Rate Function

The Rate function calculates the interest rate per period for a loan or annuity. This function returns a Double and requires the form

 Rate(nper, pmt, pv[, fv[, type[, guess]]]) 

where nper is a Double that specifies the total number of periods, pmt is a Double that specifies the payment amount per period, and pv is a Double that identifies the present value. The three optional arguments, fv, type, and guess, specify the future value, determine whether the payments are due at the start or the end of the period, and present an estimate of the function's resulting value. The first two optional arguments, fv and type are Variants; guess is a Double.

The Syd Function

The Syd function calculates the sum-of-years' digits depreciation of an asset for a specific period. This function returns a Double and uses the form

 Syd(cost, salvage, life, period) 

where cost is a Double that specifies the asset's initial cost, salvage is a Double that indicates the asset's value at the end of its useful life, life is a Double that identifies the length of the asset's useful life, and period is a Double that represents the period for which the depreciation is being calculated.

A Financial Function Example

Access users often forget that the financial functions even exist and reach for Excel when they need to analyze some figures. Depending on your needs, Excel might very well be the best tool for the job, but Access uses the same functions it just presents the data differently.

Let's suppose you want to take out a small business loan to purchase new computer equipment so you can expand the business. A flexible function procedure can calculate your monthly payments on any loan. You plug in the numbers and VBA does the work. To create this function, return to the VBE and the Chapter5 module (or open a new module if you like). Then, complete the following steps:

1. Enter the following procedure
   
   

   
   

    Public Function CalPayment(rate As Double, _  nper As Integer, pv As Double) As Currency   CalPayment = Int(Pmt(rate / 12, nper, pv)) End Function 

   
   

   NOTE

   The code in the accompanying example includes an underscore character (_) at the end of the first line. That's what is known as the line continuation character. Use this character at the end of a line when you want to continue a line of code to the next line. Including this character lets VBA know that the current line and the next are part of the same statement and should be evaluated as such.

2. In the Immediate window, enter the following statement and press Enter:
   
   

   
   

    ?CalPayment(.07, 48, 10000) 

   
   

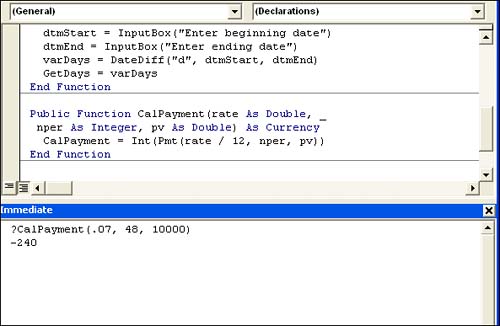
Figure 5.10 shows the approximate monthly payment (without fees) of $240. Are you curious how VBA knew to display the amount as a currency? Look at the function's first line

 Public Function CalPayment(rate As Double, _  nper As Integer, pv As Double) As Currency 

Figure 5.10. A quick procedure can calculate a monthly payment.

The As Currency phrase returns the function's value as a Currency data type. The Int function forces a whole number.

A quick function procedure can help you determine whether to go loan shopping. Simply pass different values to the function to change the payment amount. Perhaps you think you can get a better interest rate and consequently, borrow more money. If this were a task you were going to incorporate into your database, you'd create a form to gather all those values, but for now, the VBE does the trick without any special interface objects.