5.2 Programming in the Lambda-Calculus

< Free Open Study >

The lambda-calculus is much more powerful than its tiny definition might suggest. In this section, we develop a number of standard examples of programming in the lambda-calculus. These examples are not intended to suggest that the lambda-calculus should be taken as a full-blown programming language in its own right-all widely used high-level languages provide clearer and more efficient ways of accomplishing the same tasks-but rather are intended as warm-up exercises to get the feel of the system.

Multiple Arguments

To begin, observe that the lambda-calculus provides no built-in support for multi-argument functions. Of course, this would not be hard to add, but it is even easier to achieve the same effect using higher-order functions that yield functions as results. Suppose that s is a term involving two free variables x and y and that we want to write a function f that, for each pair (v,w) of arguments, yields the result of substituting v for x and w for y in s. Instead of writing f = λ(x,y).s, as we might in a richer programming language, we write f = λx.λy.s. That is, f is a function that, given a value v for x, yields a function that, given a value w for y, yields the desired result. We then apply f to its arguments one at a time, writing f v w (i.e., (f v) w), which reduces to ((λy.[x ↦ v]s) w) and thence to [y ↦ w][x ↦ v]s. This transformation of multi-argument functions into higher-order functions is called currying in honor of Haskell Curry, a contemporary of Church.

Church Booleans

Another language feature that can easily be encoded in the lambda-calculus is boolean values and conditionals. Define the terms tru and fls as follows:

   tru = λt. λf. t;   fls = λt. λf. f;

(The abbreviated spellings of these names are intended to help avoid confusion with the primitive boolean constants true and false from Chapter 3.)

The terms tru and fls can be viewed as representing the boolean values "true" and "false," in the sense that we can use these terms to perform the operation of testing the truth of a boolean value. In particular, we can use application to define a combinator test with the property that test b v w reduces to v when b is tru and reduces to w when b is fls.

   test = λl. λm. λn. l m n;

The test combinator does not actually do much: test b v w just reduces to b v w. In effect, the boolean b itself is the conditional: it takes two arguments and chooses the first (if it is tru) or the second (if it is fls). For example, the term test tru v w reduces as follows:

	test tru v w
=	(λl. λm. λn. l m n) tru v w	by definition
→	(λm. λn. tru m n) v w	reducing the underlined redex
→	(λn. tru v n) w	reducing the underlined redex
→	tru v w	reducing the underlined redex
=	(λt.λf.t) v w	by definition
→	(λf. v) w	reducing the underlined redex
→	v	reducing the underlined redex

We can also define boolean operators like logical conjunction as functions:

   and = λb. λc. b c fls;

That is, and is a function that, given two boolean values b and c, returns c if b is tru and fls if b is fls; thus and b c yields tru if both b and c are tru and fls if either b or c is fls.

   and tru tru; ▸ (λt. λf. t)   and tru fls; ▸ (λt. λf. f)

5.2.1 Exercise [⋆]

Define logical or and not functions.

Pairs

Using booleans, we can encode pairs of values as terms.

   pair = λf.λs.λb. b f s;   fst = λp. p tru;   snd = λp. p fls;

That is, pair v w is a function that, when applied to a boolean value b, applies b to v and w. By the definition of booleans, this application yields v if b is tru and w if b is fls, so the first and second projection functions fst and snd can be implemented simply by supplying the appropriate boolean. To check that fst (pair v w) →* v, calculate as follows:

	fst (pair v w)
=	fst ((λf. λs. λb. b f s) v w)	by definition
→	fst ((λs. λb. b v s) w)	reducing the underlined redex
→	fst (λb. b v w)	reducing the underlined redex
=	(λp. p tru) (λb. b v w)	by definition
→	(λb. b v w) tru	reducing the underlined redex
→	tru v w	reducing the underlined redex
→*	v	as before.

Church Numerals

Representing numbers by lambda-terms is only slightly more intricate than what we have just seen. Define the Church numerals c₀, c₁, c₂, etc., as follows:

   c₀ = λs. λz. z;   c₁ = λs. λz. s z;   c₂ = λs. λz. s (s z);   c₃ = λs. λz. s (s (s z));   etc.

That is, each number n is represented by a combinator c_n that takes two arguments, s and z (for "successor" and "zero"), and applies s, n times, to z. As with booleans and pairs, this encoding makes numbers into active entities: the number n is represented by a function that does something n times-a kind of active unary numeral.

(The reader may already have observed that c₀ and fls are actually the same term. Similar "puns" are common in assembly languages, where the same pattern of bits may represent many different values-an int, a float, an address, four characters, etc.-depending on how it is interpreted, and in low-level languages such as C, which also identifies 0 and false.)

We can define the successor function on Church numerals as follows:

   scc = λn. λs. λz. s (n s z);

The term scc is a combinator that takes a Church numeral n and returns another Church numeral-that is, it yields a function that takes arguments s and z and applies s repeatedly to z. We get the right number of applications of s to z by first passing s and z as arguments to n, and then explicitly applying s one more time to the result.

5.2.2 Exercise [⋆⋆]

Find another way to define the successor function on Church numerals.

Similarly, addition of Church numerals can be performed by a term plus that takes two Church numerals, m and n, as arguments, and yields another Church numeral-i.e., a function-that accepts arguments s and z, applies s iterated n times to z (by passing s and z as arguments to n), and then applies s iterated m more times to the result:

   plus = λm. λn. λs. λz. m s (n s z);

The implementation of multiplication uses another trick: since plus takes its arguments one at a time, applying it to just one argument n yields the function that adds n to whatever argument it is given. Passing this function as the first argument to m and c₀ as the second argument means "apply the function that adds n to its argument, iterated m times, to zero," i.e., "add together m copies of n.

   times = λm. λn. m (plus n) c₀;

5.2.3 Exercise [⋆⋆]

Is it possible to define multiplication on Church numerals without using plus?

5.2.4 Exercise [Recommended, ⋆⋆]

Define a term for raising one number to the power of another.

To test whether a Church numeral is zero, we must find some appropriate pair of arguments that will give us back this information-specifically, we must apply our numeral to a pair of terms zz and ss such that applying ss to zz one or more times yields fls, while not applying it at all yields tru. Clearly, we should take zz to be just tru. For ss, we use a function that throws away its argument and always returns fls:

   iszro = λm. m (λx. fls) tru;   iszro c₁; ▸  (λt. λf. f)   iszro (times c₀  c₂); ▸  (λt. λf. t)

Surprisingly, subtraction using Church numerals is quite a bit more difficult than addition. It can be done using the following rather tricky "predecessor function," which, given c₀ as argument, returns c₀ and, given c_i+1, returns c_i:

   zz = pair c₀ c₀;   ss = λp. pair (snd p) (plus c₁ (snd p));   prd = λm. fst (m ss zz);

This definition works by using m as a function to apply m copies of the function ss to the starting value zz. Each copy of ss takes a pair of numerals pair c_i c_j as its argument and yields pair c_j c_j+1 as its result (see Figure 5-1). So applying ss, m times, to pair c₀ c₀yields pair c₀ c₀ when m = 0 and pair c_m-1 c_m when m is positive. In both cases, the predecessor of m is found in the first component.

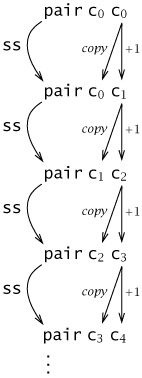
Figure 5-1: The Predecessor Function's "Inner Loop"

5.2.5 Exercise [⋆⋆]

Use prd to define a subtraction function.

5.2.6 Exercise [⋆⋆]

Approximately how many steps of evaluation (as a function of n) are required to calculate prd c_n?

5.2.7 Exercise [⋆⋆]

Write a function equal that tests two numbers for equality and returns a Church boolean. For example,

   equal c₃ c₃; ▸ (λt. λf. t)   equal c₃ c₂; ▸ (λt. λf. f)

Other common datatypes like lists, trees, arrays, and variant records can be encoded using similar techniques.

5.2.8 Exercise [Recommended, ⋆⋆⋆]

A list can be represented in the lambda-calculus by its fold function. (OCaml's name for this function is fold_left; it is also sometimes called reduce.) For example, the list [x,y,z] becomes a function that takes two arguments c and n and returns c x (c y (c z n))). What would the representation of nil be? Write a function cons that takes an element h and a list (that is, a fold function) t and returns a similar representation of the list formed by prepending h to t. Write isnil and head functions, each taking a list parameter. Finally, write a tail function for this representation of lists (this is quite a bit harder and requires a trick analogous to the one used to define prd for numbers).

Enriching the Calculus

We have seen that booleans, numbers, and the operations on them can be encoded in the pure lambda-calculus. Indeed, strictly speaking, we can do all the programming we ever need to without going outside of the pure system. However, when working with examples it is often convenient to include the primitive booleans and numbers (and possibly other data types) as well. When we need to be clear about precisely which system we are working in, we will use the symbol λ for the pure lambda-calculus as defined in Figure 5-3 and λNB for the enriched system with booleans and arithmetic expressions from Figures 3-1 and 3-2.

In λNB, we actually have two different implementations of booleans and two of numbers to choose from when writing programs: the real ones and the encodings we've developed in this chapter. Of course, it is easy to convert back and forth between the two. To turn a Church boolean into a primitive boolean, we apply it to true and false:

   realbool = λb. b true false;

To go the other direction, we use an if expression:

   churchbool = λb. if b then tru else fls;

We can build these conversions into higher-level operations. Here is an equality function on Church numerals that returns a real boolean:

   realeq = λm. λn. (equal m n) true false;

In the same way, we can convert a Church numeral into the corresponding primitive number by applying it to succ and 0:

   realnat = λm. m (λx. succ x) 0;

We cannot apply m to succ directly, because succ by itself does not make syntactic sense: the way we defined the syntax of arithmetic expressions, succ must always be applied to something. We work around this by packaging succ inside a little function that does nothing but return the succ of its argument.

The reasons that primitive booleans and numbers come in handy for examples have to do primarily with evaluation order. For instance, consider the term scc c₁. From the discussion above, we might expect that this term should evaluate to the Church numeral c₂. In fact, it does not:

   scc c₁; ▸ (λs. λz. s ((λs'. λz'. s' z') s z))

This term contains a redex that, if we were to reduce it, would bring us (in two steps) to c₂, but the rules of call-by-value evaluation do not allow us to reduce it yet, since it is under a lambda-abstraction.

There is no fundamental problem here: the term that results from evaluation of scc c₁ is obviously behaviorally equivalent to c₂, in the sense that applying it to any pair of arguments v and w will yield the same result as applying c₂ to v and w. Still, the leftover computation makes it a bit diffcult to check that our scc function is behaving the way we expect it to. For more complicated arithmetic calculations, the diffculty is even worse. For example, times c₂ c₂ evaluates not to c₄ but to the following monstrosity:

   times c₂ c₂; ▸ (λs.      λz.        (λs'. λz'. s' (s' z')) s        ((λs'.            λz'.              (λs". λz". s" (s" z")) s'              ((λs". λz".z") s' z'))       s       z))

One way to check that this term behaves like c₄ is to test them for equality:

   equal c₄ (times c₂ c₂); ▸ (λt. λf. t)

But it is more direct to take times c₂ c₂ and convert it to a primitive number:

   realnat (times c₂ c₂); ▸ 4

The conversion has the effect of supplying the two extra arguments that times c₂ c₂ is waiting for, forcing all of the latent computation in its body.

Recursion

Recall that a term that cannot take a step under the evaluation relation is called a normal form. Interestingly, some terms cannot be evaluated to a normal form. For example, the divergent combinator

   omega = (λx. x x) (λx. x x);

contains just one redex, and reducing this redex yields exactly omega again! Terms with no normal form are said to diverge.

The omega combinator has a useful generalization called the fixed-point combinator,^[7] which can be used to help define recursive functions such as factorial.^[8]

   fix = λf. (λx. f (λy. x x y)) (λx. f (λy. x x y));

Like omega, the fix combinator has an intricate, repetitive structure; it is difficult to understand just by reading its definition. Probably the best way of getting some intuition about its behavior is to watch how it works on a specific example.^[9] Suppose we want to write a recursive function definition of the form h = <body containing h>-i.e., we want to write a definition where the term on the right-hand side of the = uses the very function that we are defining, as in the definition of factorial on page 52. The intention is that the recursive definition should be "unrolled" at the point where it occurs; for example, the definition of factorial would intuitively be

   if n=0 then 1   else n * (if n-1=0 then 1             else (n-1) * (if (n-2)=0 then 1                           else (n-2) * ...))

or, in terms of Church numerals:

   if realeq n c₀ then c₁   else times n (if realeq (prd n) c₀ then c₁                 else times (prd n)                            (if realeq (prd (prd n)) c₀ then c₁                             else times (prd (prd n)) ...))

This effect can be achieved using the fix combinator by first defining g = λf. <body containing f> and then h = fix g. For example, we can define the factorial function by

   g = λfct. λn. if realeq n c₀ then c₁ else (times n (fct (prd n)));   factorial = fix g;

Figure 5-2 shows what happens to the term factorial c₃ during evaluation. The key fact that makes this calculation work is that fct n →* g fct n. That is, fct is a kind of "self-replicator" that, when applied to an argument, supplies itself and n as arguments to g. Wherever the first argument to g appears in the body of g, we will get another copy of fct, which, when applied to an argument, will again pass itself and that argument to g, etc. Each time we make a recursive call using fct, we unroll one more copy of the body of g and equip it with new copies of fct that are ready to do the unrolling again.

Figure 5-2: Evaluation of factorial c₃

5.2.9 Exercise [⋆]

Why did we use a primitive if in the definition of g, instead of the Church-boolean test function on Church booleans? Show how to define the factorial function in terms of test rather than if.

5.2.10 Exercise [⋆⋆]

Define a function churchnat that converts a primitive natural number into the corresponding Church numeral.

5.2.11 Exercise [Recommended, ⋆⋆]

Use fix and the encoding of lists from Exercise 5.2.8 to write a function that sums lists of Church numerals.

Representation

Before leaving our examples behind and proceeding to the formal definition of the lambda-calculus, we should pause for one final question: What, exactly, does it mean to say that the Church numerals represent ordinary numbers?

To answer, we first need to remind ourselves of what the ordinary numbers are. There are many (equivalent) ways to define them; the one we have chosen here (in Figure 3-2) is to give:

a constant 0,
an operation iszero mapping numbers to booleans, and
two operations, succ and pred, mapping numbers to numbers.

The behavior of the arithmetic operations is defined by the evaluation rules in Figure 3-2. These rules tell us, for example, that 3 is the successor of 2, and that iszero 0 is true.

The Church encoding of numbers represents each of these elements as a lambda-term (i.e., a function):

The term c₀ represents the number 0.

As we saw on page 64, there are also "non-canonical representations" of numbers as terms. For example, λs. λz. (λx. x) z, which is behaviorally equivalent to c₀, also represents 0.
The terms scc and prd represent the arithmetic operations succ and pred, in the sense that, if t is a representation of the number n, then scc t evaluates to a representation of n + 1 and prd t evaluates to a representation of n - 1 (or of 0, if n is 0).
The term iszro represents the operation iszero, in the sense that, if t is a representation of 0, then iszro t evaluates to true,^[10] and if t represents any number other than 0, then iszro t evaluates to false.

Putting all this together, suppose we have a whole program that does some complicated calculation with numbers to yield a boolean result. If we replace all the numbers and arithmetic operations with lambda-terms representing them and evaluate the program, we will get the same result. Thus, in terms of their effects on the overall results of programs, there is no observable difference between the real numbers and their Church-numeral representation.

^[7]It is often called the call-by-value Y-combinator. Plotkin (1975) called it Z.

^[8]Note that the simpler call-by-name fixed point combinator

     Y = λf. (λx. f (x x)) (λx. f (x x))

is useless in a call-by-value setting, since the expression Y g diverges, for any g.

^[9]It is also possible to derive the definition of fix from first principles (e.g., Friedman and Felleisen, 1996, Chapter 9), but such derivations are also fairly intricate.

^[10]Strictly speaking, as we defined it, iszro t evaluates to a representation of true as another term, but let's elide that distinction to simplify the present discussion. An analogous story can be given to explain in what sense the Church booleans represent the real ones.

< Free Open Study >