28.3 Subtyping in Kernel F:
|
| < Free Open Study > |
|
28.3 Subtyping in Kernel F<:
In §16.1, we remarked that the declarative subtype relation for the simply typed lambda-calculus with subtyping is not syntax directed—i.e., it cannot be read directly as a subtyping algorithm—for two reasons: (1) the conclusions of S-REFL and S-TRANS overlap with the other rules (so, reading the rules from bottom to top, we would not know which one to try to apply), and (2) the premises of S-TRANS mention a metavariable that does not appear in the conclusion (which a naive algorithm would have to somehow "guess"). We saw that these problems can be fixed by simply dropping the two offending rules from the system, but that, before doing so, we must fix up the system a little by combining the three separate record subtyping rules into one.
For kernel F<:, the story is similar. Again, the offending rules are S-REFL and S-TRANS, and we obtain an algorithm by dropping these rules and fixing up the remaining rules a little to account for the essential uses of the dropped rules.
In the simply typed lambda-calculus with subtyping, there were no essential uses of the reflexivity rule—we could just drop it without changing the set of derivable subtyping statements (Lemma 16.1.2, part 1). In F<:, on the other hand, subtyping statements of the form Г ⊢ X <: X can be proved only by reflexivity. So, when we remove the full reflexivity rule, we should add in its place a restricted reflexivity axiom that applies only to variables.
Г ⊢ X <:X Similarly, to eliminate S-TRANS, we must first understand which of its uses are essential. Here, the interesting interaction is with the S-TVAR rule, which allows assumptions about type variables to be used in deriving subtyping statements. For example, if Г = W<:Top, X<:W, Y<:X, Z<:Y, then the statement Г ⊢ Z <: W cannot be proved if S-TRANS is removed from the system. An instance of S-TRANS whose left-hand subderivation is an instance of the axiom S-TVAR, as in
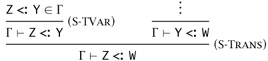
cannot, in general, be eliminated.
Fortunately, derivations of this form are the only essential uses of transitivity in subtyping. This observation can be made precise by introducing a new subtyping rule
![]()
that captures exactly this pattern of variable lookup followed by transitivity, and showing that replacing the transitivity and variable rules by this one does not change the set of derivable subtyping statements.
These changes lead us to the algorithmic subtype relation for kernel F<:, shown in Figure 28-3. We add an arrowhead to the turnstile symbol in algorithmic typing statements so that we can distinguish them from original typing statements in discussions involving both.
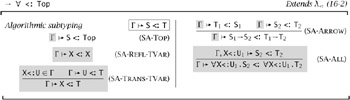
Figure 28-3: Algorithmic Subtyping for Kernel F<:
The fact that the new SA-REFL-TVAR and SA-TRANS-TVAR rules are sufficient replacements for the old reflexivity and transitivity rules is captured by the next two lemmas.
28.3.1 Lemma [Reflexivity of the Algorithmic Subtype Relation]:
![]() is provable for every Г and T.
is provable for every Г and T.
Proof: By induction on T.
28.3.2 Lemma [Transitivity of the Algorithmic Subtype Relation]:
If ![]()
![]() and
and ![]() , then
, then ![]() .
.
Proof: By induction on the sum of the sizes of the two derivations. Given two derivations, we proceed by a case analysis of the final rules in both.
If the right-hand derivation is an instance of SA-TOP, then we are done, since Г ⊢ S <: Top by SA-TOP. If the left-hand derivation is an instance of SA-Top, then Q = Top and by looking at the algorithmic rules we see that the right-hand derivation must also be an instance of SA-TOP.
If either derivation is an instance of SA-REFL-TVAR, then we are again done since the other derivation is exactly the desired result.
If the left-hand derivation ends with an instance of SA-TRANS-TVAR, then S = Y with Y<:U Î Г and we have a subderivation with conclusion Г ⊢ U <: Q. By the induction hypothesis, ![]() , and, by SA-TRANS-TVAR again,
, and, by SA-TRANS-TVAR again, ![]()
![]() , as required.
, as required.
If the left-hand derivation ends with an instance of SA-ARROW, then we have S = S1 → S2 and Q = Q1 → Q2, with subderivations ![]() and
and ![]() . But since we have already considered the case where the right-hand derivation is SA-TOP, the only remaining possibility is that this derivation also ends with SA-ARROW; we therefore have T = T1 → T2 and two more subderivations
. But since we have already considered the case where the right-hand derivation is SA-TOP, the only remaining possibility is that this derivation also ends with SA-ARROW; we therefore have T = T1 → T2 and two more subderivations ![]() and
and ![]() . We now apply the induction hypothesis twice, obtaining
. We now apply the induction hypothesis twice, obtaining ![]() and
and ![]() . SA-ARROW now yields
. SA-ARROW now yields ![]() , as required.
, as required.
If the case where the left-hand derivation ends with an instance of SA-ALL, the argument is similar. We have S = "X<:U1.S2 and Q = "X<:U1.Q2, with a subderivation Г, ![]() . But again, since we have already considered the case where the right-hand derivation is SA-TOP, it must end with SA-ALL; so T = "X<:U1.T2 with a subderivation Г
. But again, since we have already considered the case where the right-hand derivation is SA-TOP, it must end with SA-ALL; so T = "X<:U1.T2 with a subderivation Г ![]() . We apply the induction hypothesis to obtain Г
. We apply the induction hypothesis to obtain Г ![]() , and SA-ALL to obtain
, and SA-ALL to obtain ![]() .
.
28.3.3 Theorem [Soundness and Completeness of Algorithmic Subtyping]:
Г ⊢ S <: T iff ![]() .
.
Proof: Both directions proceed by induction on derivations. Soundness (⇐) is routine. Completeness (⇒) relies on Lemmas 28.3.1 and 28.3.2.
Finally, we need to check that the subtyping rules define an algorithm that is total—i.e., that terminates on all inputs. We do this by assigning a weight to each subtyping statement and checking that the algorithmic rules all have conclusions with strictly greater weight than their premises.
28.3.4 Definition:
The weight of a type T in a context Г, written weightГ(T), is defined as follows:
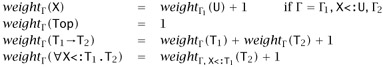
The weight of a subtyping statement Г ⊢ S <: T is the maximum weight of S and T in Г.
28.3.5 Theorem:
The subtyping algorithm terminates on all inputs.
Proof: The weight of the conclusion in an instance of any of the algorithmic subtyping rules is strictly greater than the weight of any of the premises.
28.3.6 Corollary:
Subtyping in kernel F<: is decidable.
|
| < Free Open Study > |
|
EAN: 2147483647
Pages: 262