28.4 Subtyping in Full F:

< Free Open Study >

28.4 Subtyping in Full F_<:

The subtype checking algorithm for full F_<:, summarized in Figure 28-4, is nearly the same as for kernel F_<:: the only change is replacing SA-ALL with its more flexible variant. As with kernel F_<:, the soundness and completeness of this algorithmic relation with respect to the original subtype relation follow directly from the fact that the algorithmic relation is reflexive and transitive.

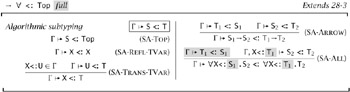
Figure 28-4: Algorithmic Subtyping for Full F_<:

For reflexivity, the argument is exactly the same as before, but transitivity is a bit more delicate. To see why, recall the proof of transitivity for kernel F_<: from the previous section (Lemma 28.3.2). The idea there was to take two subtyping derivations ending with the statements Г ⊢ S <: Q and Г ⊢ Q <: T, and to show how to rearrange and reassemble their subderivations to construct a derivation of Г ⊢ S <: T without using the transitivity rule, given (as an induction hypothesis) that it is possible to do the same with pairs of smaller derivations. Now, suppose we have two derivations ending with the new SA-ALL rule:

⋮	⋮	⋮	⋮
Г ⊢ Q₁ <: S₁	Г, X<:Q₁ ⊢ S₂ <: Q₂	Г ⊢ T₁ <: Q₁	Г, X<:T₁ ⊢ Q₂ <: T₂
Г ⊢ "X<:S₁.S₂ <: "X<:Q₁.Q₂		Г ⊢ "X<:Q₁.Q₂ <: "X<:T₁.T₂

Following the pattern of the earlier proof, we would like to use the induction hypothesis to combine the left-and right-hand subderivations and finish with a single use of SA-ALL with the conclusion Г ⊢ "X<:S₁.S₂ <: "X<:T₁.T₂. For the left-hand subderivations, there is no problem; the induction hypothesis gives us a transitivity-free derivation of Г ⊢ T₁ <: S₁. For the right-hand subderivations, however, the induction hypothesis does not apply because the contexts in the subderivations are different-the upper bound for X is Q₁ in one and T₁ in the other.

Fortunately, we know a way to make the contexts the same: the narrowing property from Chapter 26 (Lemma 26.4.5) tells us that a valid subtyping statement remains valid if we replace a bound in the context by one of its subtypes. So it would seem we can just narrow the subderivation of Г, X<:Q₁ ⊢ S₂ <: Q₂ to Г, X<:T₁ ⊢ S₂ <: Q₂, thereby enabling the induction hypothesis.

However, we need to be a little careful. Lemma 26.4.5 shows that we can take any derivation and construct a derivation with a narrowed conclusion, but it does not guarantee that the new derivation will be the same size as the old one. Indeed, if we examine the lemma's proof, it is clear that narrowing generally yields a bigger derivation, since it involves splicing in a copy of an arbitrarily large derivation at each place where the S-TVAR axiom is used to look up the variable being narrowed. Moreover, this splicing operation involves creating new instances of transitivity, which is precisely the rule that we are trying to show is admissible in the present system.

The solution to these difficulties is to prove transitivity and narrowing together, using an induction hypothesis based on the size of the intermediate type Q in the transitivity property and the original bound Q in the narrowing property.

We preface this argument with an easy lemma recording the fact that permuting the order or adding fresh type variable bindings to the context does not invalidate any derivable subtyping statements.

28.4.1 Lemma [Permutation and Weakening]:

Suppose that Г is a well-formed permutation of Г (cf. 26.4.1). If 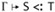, then .
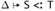If 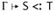and dom(Δ) ∩ dom(Г) = , then Г, .

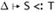Proof: Routine inductions. Part (1) is used in the SA-ALL case of part (2).

28.4.2 Lemma [Transitivity and Narrowing for Full F_<:]:

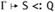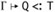If and , then .
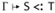If Г, X<:Q, 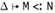and 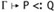then Г, X<:P, .

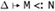Proof: The two parts are proved simultaneously, by induction on the size of Q. At each stage of the induction, the argument for part (2) assumes that part (1) has been established already for the Q in question; part (1) uses part (2) only for strictly smaller Qs.

We proceed by an inner induction on the size of the first given derivation, with a case analysis on the final rules in both derivations. All but one of the cases are like the proof of Lemma 28.3.2; the difference is in the SA-ALL case.

If the right-hand derivation is an instance of SA-TOP, then we are done, since Г ⊢ S <: Top by SA-TOP. If the left-hand derivation is an instance of SA-TOP, then Q = Top, and, inspecting the algorithmic rules, we see that the right-hand derivation must also be an instance of SA-TOP. If either derivation is an instance of SA-REFL-TVAR, then we are again done, since the other derivation is exactly the desired result.

If the left-hand derivation ends with an instance of SA-TRANS-TVAR, then we have S = Y with Y<:U Î Г and a subderivation of Г ⊢ U <: Q. By the inner induction hypothesis, , and, by SA-TRANS-TVAR again, 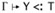, as required.

If the left-hand derivation ends with an instance of SA-ARROW or SA-ALL, then, since we have already considered the case where the right-hand derivation ends with SA-TOP, it must end with the same rule as the left. If this rule is SA-ARROW, then we have S = S₁→S₂, Q = Q₁→Q₂, and T = T₁→T₂, with subderivations 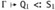, , 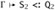, 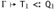and 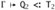. We apply part (1) of the outer induction hypothesis twice (noting that Q₁ and Q₂ are both smaller than Q) to obtain and , and then use SA-ARROW to obtain .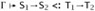

In the case where the two derivations end with SA-ALL, we have S = "X<:S₁.S₂, Q = "X<:Q₁.Q₂, and T = "X<:T₁.T₂, with

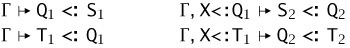
as subderivations. By part (1) of the outer induction hypothesis (Q₁ being smaller than Q), we can combine the two subderivations for the bounds to obtain 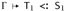. For the bodies, we need to work a little harder, since the two contexts do not quite agree. We first use part (2) of the outer induction hypothesis (noting again that Q₁ is smaller than Q) to narrow the bound of X in the derivation of Г, 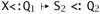, obtaining Г,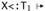 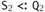. Now part (1) of the outer induction hypothesis applies (Q₂ being smaller than Q), yielding Г, 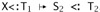. Finally, by SA-ALL, .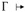
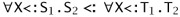We again proceed by an inner induction on the size of the first given derivation, with a case analysis on the final rule of this derivation. Most of the cases proceed by straightforward use of the inner induction hypothesis. The interesting case is SA-TRANS-TVAR with M = X and we have Г, 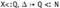as a subderivation. Applying the inner induction hypothesis to this subderivation yields Г, 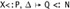. Also, applying weakening (Lemma 28.4.1, part 2) to the second given derivation yields Г, 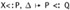. Now, by part (1) of the outer induction hypothesis (with the same Q), we have Г, 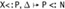. Rule SA-TRANS-TVAR yields Г, 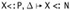, as required.

28.4.3 Exercise [⋆⋆⋆⋆ ↛]:

There is another reasonable variant of the quantifier subtyping rule that is a bit more flexible than the kernel F_<: rule but sub-stantially less so than the full F_<: rule:

This rule is close to the kernel F_<: variant, but instead of requiring that the bounds of the two quantifiers be syntactically identical, it demands only that they be equivalent-each a subtype of the other. The difference between the kernel rule and this one actually appears only when we enrich the language with some construct whose subtyping rules generate non-trivial equivalence classes, such as records. For example, in pure kernel F_<: with records, the type "X<:{a:Top,b:Top}.X would not be a subtype of "X<:{b:Top,a:Top}.X, whereas with the above rule it would be. Is subtyping decidable for the system with this rule?

< Free Open Study >