6.4 Montgomery Reduction and Exponentiation

Team-Fly

6.4 Montgomery Reduction and Exponentiation

Now we are going to abandon addition chains and turn our attention to another idea, one that is interesting above all from the algebraic point of view. It makes it possible to replace multiplications modulo an odd number n by multiplications modulo a power of 2, that is, 2^k, which requires no explicit division and is therefore more efficient than a reduction modulo an arbitrary number n. This useful method for modular reduction was published in 1985 by P. Montgomery [Mont] and since then has found wide practical application. It is based on the following observation.

Let n and r be relatively prime integers, and let r⁻¹ be the multiplicative inverse of r modulo n; and likewise let n⁻¹ be the multiplicative inverse of n modulo r; and furthermore, define n′ := −n⁻¹ mod r and m := tn′ mod r. For integers t we then have

(6.8)

Note that on the left side of the congruence we have taken congruences modulo r and a division by r (note that t + mn ≡ 0 mod r, so the division has no remainder), but we have not taken congruences modulo n. By choosing r as a power of 2 in the form 2^s we can reduce a number x modulo r simply by slicing off x at the sth bit (counting from the least-significant bit), and we can carry out the division of x by r by shifting x to the right by s bit positions. The left side of (6.8) thus requires significantly less computational expense than the right side, which is what gives the equation its charm. For the two required operations we can invoke the functions mod2_l() (cf. Section 4.3) and shift_l() (cf. Section 7.1).

This principle of carrying out reduction modulo n is called Montgomery reduction. Below, we shall institute Montgomery reduction for the express purpose of speeding up modular exponentiation significantly in comparison to our previous results. Since the procedure requires that n and r be relatively prime, we must take n to be odd. First we have to deal with a couple of considerations.

We can clarify the correctness of the previous congruence with the help of some simple checking. Let us replace m on the left-hand side of (6.8) by the expression tn′ mod r, which is (6.9), and further, replace tn′ mod r by tn′ − r ⌊tn′/r⌋ Î to get (6.10), and then in (6.10) for n′ the integer expression (r′r − 1)/n for a certain r′ Î and obtain (6.11). After reduction modulo n we obtain the result (6.12):

(6.9)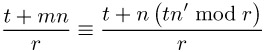

(6.10)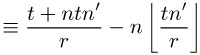

(6.11)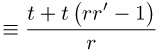

(6.12)

To summarize equation (6.8) we record the following: Let n, t, r Î with gcd(n, r) = 1, n′ := −n⁻¹ mod r. For

(6.13)

we have

(6.14)

(6.15)

We shall return to this result later.

To apply Montgomery reduction we shift our calculations modulo n into a complete residue system (cf. Chapter 5)

with a suitable r := 2^s > 0 such that 2^s−1 ≤ n < 2^s. Then we define the Montgomery product "×" of two numbers a and b in R:

with r⁻¹ representing the multiplicative inverse of r modulo n. We have

and thus the result of applying × to members of R is again in R. The Montgomery product is formed by applying Montgomery reduction, where again n′ := −n⁻¹ mod r. From n′ we derive the representation 1 = gcd(n, r) = r′r − n′n, which we calculate in anticipation of Section 10.2 with the help of the extended Euclidean algorithm. From this representation of 1 we immediately obtain

and

so that r′ = r⁻¹ mod n is the multiplicative inverse of r modulo n, and n′ = −n⁻¹ mod r the negative of the inverse of n modulo r (we are anticipating somewhat; cf. Section 10.2). The calculation of the Montgomery product now takes place according to the following algorithm.

Calculation of the Montgomery product a × b in R(r, n)

Set t ← ab.
Set m ← tn′ mod r.
Set u ← (t + mn)/r (the quotient is an integer; see above).
If u ≥ n, output u − n, and otherwise u. Based on the above selection of the parameter we have a, b < n as well as m, n < r and finally u < 2n; cf. (6.21).

The Montgomery product requires three long-integer multiplications, one in step 1 and two for the reduction in steps 2 and 3. An example with small numbers will clarify the situation: Let a = 386, b = 257, and n = 533. Further, let r = 2¹⁰. Then n′ = −n⁻¹ mod r = 707, m = 6, t + mn = 102400, and u = 100.

A modular multiplication ab mod n with odd n can now be carried out by first transforming a′ ← ar mod n and b′ ← br mod n to R, there forming the Montgomery product p′ ← a′ × b′ = a′b′r⁻¹ mod n and then with p ← p′ × 1 = p′r⁻¹ = ab mod n obtaining the desired result. However, we can spare ourselves the reverse transformation effected in the last step by setting p ← a′ × b at once and thus avoid the transformation of b, so that in the end we have the following algorithm.

Calculation of p = ab mod n (n odd) with the Montgomery product

Determine r := 2^s with 2^s−1 ≤ n < 2^s. Calculate 1 = r′r − n′n by means of the extended Euclidean algorithm.
Set a′ ← ar mod n.
Set p ← a′ × b and output p.

Again we present an example with small numbers for clarification: Let a = 123, b = 456, n = 789, r = 2¹⁰. Then n′ = −n⁻¹ mod r = 963, a′ = 501, and p = a′ × b = 69 = ab mod n.

Since the precalculation of r′ and n′ in steps 1 and 2 is very time-consuming and Montgomery reduction in this version also has two long-number multiplications on its balance sheet, there is actually an increased computational expenditure compared with "normal" modular multiplication, so that the computation of individual products with Montgomery reduction is not worthwhile.

However, in cases where many modular multiplications with a constant modulus are required, for which therefore the time-consuming precalculations occur only once, we may expect more favorable results. Particularly suited for the Montgomery product is modular exponentiation, for which we shall suitably modify the M-ary algorithm. To this end let once again e = (e_m−1 e_m−2...e₀)_B and n = (n_l−1 n_l−2...n₀)_B be the representations of the exponent e and the modulus n to the base B = 2^k. The following algorithm calculates powers a^e mod n in with odd n using Montgomery multiplication. The squarings that occur in the exponentiation become Montgomery products a × a, in the computation of which we can use the advantages of squaring.

Exponentiation modulo n (n odd) with the Montgomery product

Set r ← B^l = 2^kl. Calculate 1 = rr′ − nn′ with the Euclidean algorithm.
Set ā ← ar mod n. Calculate and store the powers ā³, ā⁵,..., 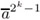using the Montgomery product × in R(r, n).
If e_m−1 ≠ 0, factor e_m−1 = 2^tu with odd u. Set ← .

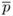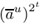If e_m−1 = 0, set 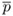← r mod n.

In each case set i ← m − 2.
If e_i = 0, set 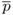← 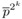= 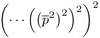(k-fold squaring = × ).

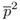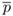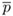If e_i ≠ 0, factor e_i = 2^tu with odd u. Set ← .
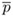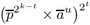If i ≥ 0, set i ← i − 1 and go to step 4.
Output the Montgomery product 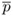× 1.

Further possibilities for improving the algorithm lie less in the exponentiation algorithm than in the implementation of the Montgomery product itself, as demonstrated by S. R. Dussé and B. S. Kaliski in [DuKa]: In calculating the Montgomery product on page 105, in step 2 we can avoid the assignment m ← tn′ mod r in the reduction modulo r. Furthermore, we can calculate with := n′ mod B instead of with n′ in executing the Montgomery reduction. We can create a digit m_i ← t_i modulo B, multiply it by n, scale by the factor Bⁱ, and add to t. To calculate ab mod n with a, b < n the modulus n has the representation n = (n_l−1n_l−2...n₀)_B as above, and we let r := B^l as well as rr′ − nn′ = 1 and := n′ mod B.

Calculation of the Montgomery product a × b à la Dussé and Kaliski

Set t ← ab, 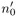← n′ mod B, i ← 0.
Set m_i ← t_i 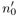mod B (m_i is a one-digit integer).
Set t ← t + m_inBⁱ.
Set i ← i + 1; if i ≤ l − 1, go to step 2.
Set t ← t/r.
If t ≥ n, output t − n and otherwise t.

Dussé and Kaliski state that the basis for their clever simplification is the method of Montgomery reduction to develop t as a multiple of r, but they offer no proof. Before we use this procedure we wish to make more precise why it suffices to calculate a × b. The following is based on a proof of Christoph Burnikel [Zieg]:

In steps 2 and 3 the algorithm calculates a sequence by means of the recursion

(6.16)

(6.17)

where

is the already familiar function that is induced by the Montgomery equation (cf. (6.13), and there set r ← B in f(t)). The members of the sequence t⁽ⁱ⁾ have the properties

(6.18)

(6.19)

(6.20)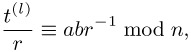

(6.21)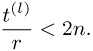

Properties (6.18) and (6.19) are derived inductively from (6.14), (6.15), (6.16), and (6.17); from (6.18) we obtain B^l | t^(l) ⇔ r | t^(l). From this and from t^(l) = ab mod n follows (6.20), and lastly we have (6.21) on account of

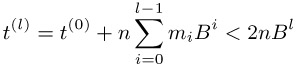
(note here that t⁽⁰⁾ = ab < n² < nB^l).

The expenditure for the reduction is now determined essentially by multiplication of numbers of order of magnitude the size of the modulus. This variant of Montgomery multiplication can be elegantly implemented in code that forms the core of the multiplication routine mul_l() (cf. page 35).

Function:	Montgomery product
Syntax:	void mulmon_l (CLINT a_l, CLINT b_l, CLINT n_l, USHORT nprime, USHORT logB_r, CLINT p_l);
Input:	a_l, b_l (factors a and b) n_l (modulus n > a, b) nprime (n′ mod B) logB_r (logarithm of r to base B = 2¹⁶; it must hold that B^logB_r−1 ≤ n < B^logB_r)
Output:	p_l (Montgomery product a × b = a · b · r⁻¹ mod n)

 void mulmon_l (CLINT a_l, CLINT b_l, CLINT n_l, USHORT nprime,          USHORT logB_r, CLINT p_l) {   CLINTD t_l;   clint *tptr_l, *nptr_l, *tiptr_l, *lasttnptr, *lastnptr;   ULONG carry;   USHORT mi;   int i;   mult (a_l, b_l, t_l);   lasttnptr = t_l + DIGITS_L (n_l);   lastnptr = MSDPTR_L (n_l);

The earlier use of the function mult() makes possible the multiplication of a_l and b_l without the possibility of overflow (see page 70); for the Montgomery squaring we simply insert sqr(). The result has sufficient space in t_l. Then t_l is given leading zeros to bring it to double the number of digits of n_l if t_l is smaller than this.

   for (i = DIGITS_L (t_l) + 1; i <= (DIGITS_L (n_l) << 1); i++)     {       t_l[i] = 0;     }   SETDIGITS_L (t_l, MAX (DIGITS_L (t_l), DIGITS_L (n_l) << 1));

Within the following double loop the partial products m_inBⁱ with m_i := t_i are calculated one after the other and added to t_l. Here again the code is essentially that of our multiplication function.

   for (tptr_l = LSDPTR_L (t_l); tptr_l <= lasttnptr; tptr_l++)     {       carry = 0;       mi = (USHORT)((ULONG)nprime * (ULONG)*tptr_l);       for (nptr_l = LSDPTR_L (n_l), tiptr_l = tptr_l;            nptr_l <= lastnptr; nptr_l++, tiptr_l++)          {            *tiptr_l = (USHORT)(carry = (ULONG)mi * (ULONG)*nptr_l +                 (ULONG)*tiptr_l + (ULONG)(USHORT)(carry >> BITPERDGT));          }

In the following inner loop a possible overflow is transported to the most-significant digit of t_l, and t_l contains an additional digit in case it is needed. This step is essential, since at the start of the main loop t_l was given a value and not initialized via multiplication by 0 as was the variable p_l.

     for ( ;          ((carry >> BITPERDGT) > 0) && tiptr_l <= MSDPTR_L (t_l);          tiptr_l++)        {         *tiptr_l = (USHORT)(carry = (ULONG)*tiptr_l +                        (ULONG)(USHORT)(carry >> BITPERDGT));        }      if (((carry >> BITPERDGT) > 0))         {           *tiptr_l = (USHORT)(carry >> BITPERDGT);           INCDIGITS_L (t_l);         }     }

Now follows division by B^l, and we shift t_l by logB_r digits to the right, or ignore the logB_r least-significant digits of t_l. Then if applicable the modulus n_l is subtracted from t_l before t_l is returned as result into p_l.

   tptr_l = t_l + (logB_r);   SETDIGIT_L (tptr_l, DIGITS_L (t_l) - (logB_r));   if (GE_L (tptr_l, n_l))     {       sub_l (tptr_l, n_l, p_l);     }   else     {       cpy_l (p_l, tptr_l);     } }

The Montgomery squaring sqrmon_l() differs from this function only marginally: There is no parameter b_l in the function call, and instead of multiplication with mult(a_l, b_l, t_l) we employ the squaring function sqr(a_l, t_l), which likewise ignores a possible overflow. However, in modular squaring in the Montgomery method one must note that after the calculation of p′ ← a′ × a′ the reverse transformation p ← p′ × 1 = p′r⁻¹ = a² mod n must be calculated explicitly (cf. page 105).

Function:	Montgomery square
Syntax:	void sqrmon_l (CLINT a_l, CLINT n_l, USHORT nprime, USHORT logB_r, CLINT p_l);
Input:	a_l (factor a), n_l (modulus n > a) nprime (n′ mod B) logB_r (logarithm of r to base B = 2¹⁶); it must hold that B^logB_r−1 ≤ n < B^logB_r
Output:	p_l (Montgomery square a²r⁻¹ mod n)

In their article Dussé and Kaliski also present the following variant of the extended Euclidean algorithm, to be dealt with in detail in Section 10.2, for calculating = n′ mod B, with which the expenditure for the precalculations can be reduced. The algorithm calculates −n⁻¹ mod 2^s for an s > 0 and for this requires long-number arithmetic.

Algorithm for calculating the inverse −n⁻¹ mod 2^s for s > 0, n odd

Set x ← 2, y ← 1, and i ← 2.
If x < ny mod x, set y ← y + x.
Set x ← 2x and i ← i + 1; if i ≤ s, go to step 2.
Output x − y.

With complete induction it can be shown that in step 2 of this algorithm yn ≡ 1 mod x always holds, and thus y ≡ n⁻¹ mod x. After x has taken on the value 2^s in step 3, we obtain with 2^s − y ≡ −n⁻¹ mod 2^s the desired result if we choose s such that 2^s = B. The short function for this can be obtained under the name invmon_l() in the FLINT/C source. It takes only the modulus n as argument and outputs the value −n⁻¹ mod B.

These considerations are borne out in the creation of the functions mexp5m_l() and mexpkm_l(), for which we give here only the interface, together with a computational example.

Function:	modular exponentiation with odd modulus (2⁵-ary or 2^k-ary method with Montgomery product)
Syntax:	int mexp5m_l (CLINT bas_l, CLINT exp_l, CLINT p_l, CLINT m_l); int mexpkm_l (CLINT bas_l, CLINT exp_l, CLINT p_l, CLINT m_l);
Input:	bas_l (base) exp_l (exponent) m_l (modulus)
Output:	p_l (power residue)
Return:	E_CLINT_OK if all is ok E_CLINT_DBZ if division by 0 E_CLINT_MAL if malloc() error E_CLINT_MOD if even modulus

These functions employ the routines invmon_l(), mulmon_l(), and sqrmon_l() to compute the Montgomery products. Their implementation is based on the functions mexp5_l() and mexpk_l() modified according to the exponentiation algorithm described above.

We would like to reconstruct the processes of Montgomery exponentiation in mexpkm_l() with the same numerical example that we looked at for M-ary exponentiation (cf. page 97). In the following steps we shall calculate the power 1234⁶⁶⁷ mod 18577:

Precomputations

The exponent e = 667 is represented to the base 2^k with k = 2 (cf. the algorithm for Montgomery exponentiation on page 111). The exponent e thereby has the representation

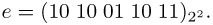
The value r for Montgomery reduction is r = 2¹⁶ = B = 65536.

The value 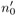(cf. page 107) is now calculated as 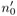= 34703.

The transformation of the base a into the residue system R(r, n) (cf. page 104) follows from

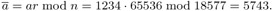
The power ā³ in R(r, n) has the value ā³ = 9227. Because of the small exponent, further powers of ā do not arise in the precomputation.

Exponentiation loop

2¹ · 1	2¹ · 1	2⁰ · 1	2¹ · 1	2⁰ · 3
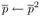
-	16994	3682	14511	11066
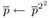
-	-	6646	-	12834
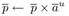
5743	15740	8707	16923	1583
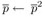
9025	11105	-	1628	-

Result

The value of the power p after normalization:

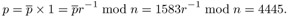
Those interested in reconstructing the coding details of the functions mexp5m_l() and mexpkm_l() and the calculational steps of the example related to the function mexpkm_l() are referred to the FLINT/C source code.

At the start of this chapter we developed the function wmexp_l(), which has the advantage for small bases that only multiplications p ← pa mod m of the type CLINT * USHORT mod CLINT occur. In order to profit from the Montgomery procedure in this function, too, we adjust the modular squaring to Montgomery squaring, as in mexpkm_l(), with the use of the fast inverse function invmon_l(), though we leave the multiplication unchanged. We can do this because with the calculational steps for Montgomery squaring and for conventional multiplication modulo n,

we do not abandon the residue system R(r, n) = {ir mod n | 0 ≤ i < n} introduced above. This process yields us both the function wmexpm_l() and the dual function umexpm_l() for USHORT exponents, respectively for odd moduli, which in comparison to the two conventional functions wmexp_l() and umexp_l() again yields a significant speed advantage. For these functions, too, we present here only the interface and a numerical example. The reader is again referred to the FLINT/C source for details.

Function:	modular exponentiation with Montgomery reduction for USHORT-base, respectively USHORT exponents and odd modulus
Syntax:	int wmexpm_l (USHORT bas, CLINT e_l, CLINT p_l, CLINT m_l); int umexpm_l (CLINT bas_l, USHORT e, CLINT p_l, CLINT m_l);
Input:	bas, bas_l (base) e, e_l (exponent) m_l (modulus)
Output:	p_l (residue of bas^e_l mod m_l, respectively of bas_l^e mod m_l)
Return:	E_CLINT_OK if all is ok E_CLINT_DBZ if division by 0 E_CLINT_MOD if even modulus

The function wmexpm_l() is tailor-made for our primality test in Section 10.5, where we shall profit from our present efforts. The function will be documented with the example used previously of the calculation of 1234⁶⁶⁷ mod 18577.

Precalculations

The binary representation of the exponent is e = (1010011011)₂.

The value r for the Montgomery reduction is r = 2¹⁶ = B = 65536.

The value 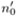(cf. page 107) is calculated as above, yielding 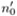= 34703.

The initial value of 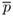is set as 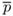← pr mod 18577.

Exponentiation loop

Exponent bit	1	0	1	0	0	1	1	0	1	1
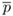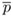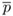← × in R(r, n)	9805	9025	16994	11105	3682	6646	14511	1628	11066	9350
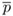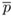← a mod n	5743	-	15740	-	-	8707	16923	-	1349	1583

Result

The value of the exponent p after normalization:

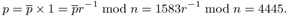
A detailed analysis of the time behavior of Montgomery reduction with the various optimizations taken into account can be found in [Boss]. There we are promised a ten to twenty percent saving in time over modular exponentiation by using Montgomery multiplication. As can be seen in the overviews in Appendix D of typical calculation times for FLINT/C functions, our implementations bear out this claim fully. To be sure, we have the restriction that the exponentiation functions that use Montgomery reduction can be used only for odd moduli. Nonetheless, for many applications, for example for encryption and decryption, as well as for computing digital signatures according to the RSA procedure (see Chapter 16), the functions mexp5m_l() and mexpkm_l() are the functions of choice.

Altogether, we have at our disposal a number of capable functions for modular exponentiation. To obtain an overview, in Table 6.5 we collect these functions together with their particular properties and domains of application.

Table 6.5: Exponentiation functions in FLINT/C
Function	Domain of application
mexp5_l()	General 2⁵-ary exponentiation, without memory allocation, greater stack requirements.
mexpk_l()	General 2^k-ary exponentiation with optimal k for CLINT numbers, with memory allocation, lower stack requirements.
mexp5m_l()	2⁵-ary Montgomery exponentiation for odd moduli, without memory allocation, greater stack requirements.
mexpkm_l()	2^k-ary Montgomery exponentiation for odd moduli, with optimal k for CLINT numbers up to 4096 binary digits, with memory allocation, lower stack requirements.
umexp_l()	Mixed binary exponentiation of a CLINT base with USHORT exponent, lower stack requirements.
umexpm_l()	Mixed binary exponentiation of a CLINT base with USHORT exponent and Montgomery reduction, thus only for odd moduli, lower stack requirements.
wmexp_l()	Mixed binary exponentiation of a USHORT base with CLINT exponent, lower stack requirements.
wmexpm_l()	Mixed binary exponentiation with Montgomery squaring of a USHORT base with CLINT exponent, odd moduli, lower stack requirements.
mexp2_l()	Mixed exponentiation with a power-of-2 exponent, lower stack requirements.

Team-Fly