6.5 Cryptographic Application of Exponentiation

Team-Fly

---

6.5 Cryptographic Application of Exponentiation

We have worked hard in this chapter in our calculation of powers, and it is reasonable to ask at this point what modular exponentiation might have to offer to cryptographic applications. The first example to come to mind is, of course, the RSA procedure, which requires a modular exponentiation for encryption and decryption—assuming suitable keys. However, the author would like to ask his readers for a bit (or perhaps even a byte) of patience, since for the RSA procedure we still must collect a few more items, which we do in the next chapter. We shall return to this extensively in Chapter 16.

For those incapable of waiting, we offer as examples of the application of exponentiation two important algorithms, namely, the procedure suggested in 1976 by Martin E. Hellman and Whitfield Diffie [Diff] for the exchange of cryptographic keys and the encryption procedure of Taher ElGamal as an extension of the Diffie-Hellman procedure.

The Diffie-Hellman procedure represents a cryptographic breakthrough, namely, the first public key, or asymmetric, cryptosystem (see Chapter 16). Two years after its publication, Rivest, Shamir, and Adleman published the RSA procedure (see [Rive]). Variants of the Diffie-Hellman procedure are used today for key distribution in the Internet communications and security protocols IPSec, IPv6, and SSL, which were developed to provide security in the transfer of data packets in the IP protocol layer and the transfer of data at the application level, for example from the realms of electronic commerce. This principle of key distribution thus has a practical significance that would be difficult to overestimate.^[2]

With the aid of the Diffie-Hellman protocol two communicators, Ms. A and Mr. B, say, can negotiate in a simple way a secret key that then can be used for the encryption of communications between the two. After A and B have agreed on a large prime number p and a primitive root a modulo p (we shall return to this below), the Diffie-Hellman protocol runs as follows.

Protocol for key exchange à la Diffie-Hellman

1. A chooses an arbitrary value x_A ≤ p − 1 and sends y_A := 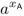mod p as her public key to B.

2. B chooses an arbitrary value x_B ≤ p − 1 and sends y_B:= 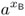mod p as his public key to A.

3. A computes the secret key s_A := 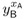mod p.

4. B computes the secret key s_B := 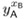mod p.

Since

after step 4, A and B are dealing with a common key. The values p and a do not have to be kept secret, nor the values y_A and y_B exchanged in steps 1 and 2. The security of the procedure depends on the difficulty in calculating discrete logarithms in finite fields, and the difficulty of breaking the system is equivalent to that of calculating values x_A or x_B from values y_A or y_B in .^[3] That the calculation of a^xy from a^x and a^y in a finite cyclic group (the Diffie-Hellman problem) is just as difficult as the calculation of discrete logarithms and thus equivalent to this problem is, in fact, conjectured but has not been proved.

To ensure the security of the procedure under these conditions the modulus p must be chosen sufficiently large (at least 1024 bits, better 2048 or more; see Table 16.1), and one should ensure that p − 1 contains a large prime divisor close to (p − 1)/2 to exclude particular calculational procedures for discrete logarithms (a constructive procedure for such prime numbers will be presented in Chapter 16 in connection with the generation of strong primes, for example for the RSA procedure).

The procedure has the advantage that secret keys can be generated as needed on an ad hoc basis, without the need for secret information to be held for a long time. Furthermore, for the procedure to be used there are no further infrastructure elements necessary for agreeing on the parameters a and b. Nonetheless, this protocol possesses some negative characteristics, the gravest of which is the lack of authentication proofs for the exchanged parameters y_A and y_B. This makes the procedure susceptible to man-in-the-middle attacks, whereby attacker X intercepts the messages of A and B with their public keys y_A and y_B and replaces them with falsified messages to A and B containing his own public key y_X.

Then A and B calculate "secret" keys := mod p and := mod p, while X on his or her part calculates from mod p and analogously. The Diffie-Hellman protocol has now been executed not between A and B, but between X and A as well as between X and B. Now X is in a position to decode messages from A or B and to replace them by falsified messages to A or B. What is fatal is that from a cryptographic point of view the participants A and B are clueless as to what has happened.

To compensate for these defects without giving up the advantages, several variants and extensions have been developed for use in the Internet. They all take into account the necessity that key information be exchanged in such a way that its authenticity can be verified. This can be achieved, for example, by the public keys being digitally signed by the participants and the associated certificate of a certification authority being sent with them (see in this regard page 339, Section 16.3), which is implemented, for example, in the SSL protocol. IPSec and IPv6 use a complexly constructed procedure with the name ISAKMP/Oakley,^[4] which overcomes all the drawbacks of the Diffie-Hellman protocol (for details see [Stal], pages 422–423).

To determine a primitive root modulo p, that is, a value a whose powers aⁱ mod p with i = 0, 1,....,p − 2 constitute the entire set of elements of the multiplicative group = { 1,...,p − 1 } (see in this regard Section10.2), the following algorithm can be used (see [Knut], Section 3.2.1.2, Theorem C). It is assumed that the prime factorization p − 1 = of the order of is known.

Finding a primitive root modulo p

1. Choose a random integer a Î [0, p − 1] and set i ← 1.

2. Compute t ← 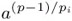mod p.

3. If t = 1, go to step 1. Otherwise, set i ← i + 1. If i ≤ k, go to step 2. If i > k, output a and terminate the algorithm.

The algorithm is implemented in the following function.

Function:	ad hoc generation of a primitive root modulo p (2 < p prime)
Syntax:	int primroot_l (CLINT a_l, unsigned noofprimes, clint **primes_l);
Input:	noofprimes (number of distinct prime factors in p − 1, the order of the group) primes_l (vector of pointers to CLINT objects, beginning with p − 1, then follow the prime divisors p1,...,pk of the group order p − 1 = , k = noofprimes)
Output:	a_l (primitive root modulo p_l)
Return:	E_CLINT_OK if all is ok −1 if p − 1 odd and thus p is not prime

 int primroot_l (CLINT a_l, unsigned int noofprimes, clint *primes_l[]) {   CLINT p_l, t_l, junk_l;   ULONG i;   if (ISODD_L (primes_l[0]))     {       return -1;     } 

primes_l[0] contains p − 1, from which we obtain the modulus in p_l.

   cpy_l (p_l, primes_l[0]);   inc_l (p_l);   SETONE_L (a_l);   do     {       inc_l (a_l); 

As candidates a for the sought-after primitive root only natural numbers greater than or equal to 2 are tested. If a is a square, then a cannot be a primitive root modulo p, since then already a^(p−1)/2 ≡ 1 mod p, and the order of a must be less than φ(p) = p − 1. In this case a_l is incremented. We test whether a_l is a square with the function issqr_l() (cf. Section 10.3).

     if (issqr_l (a_l, t_l))       {          inc_l (a_l);       }     i = 1; 

The calculation of t ← mod p takes place in two steps. All prime factors p_i are tested in turn; we use Montgomery exponentiation. If a primitive root is found, it is output in a_l.

       do          {            div_l (primes_l[0], primes_l[i++], t_l, junk_l);            mexpkm_l (a_l, t_l, t_l, p_l);          }       while ((i <= noofprimes) && !EQONE_L (t_l));     }   while (EQONE_L (t_l));   return E_CLINT_OK; } 

As a second example for the application of exponentiation we consider the encryption procedure of ElGamal, which as an extension of the Diffie-Hellman procedure also provides security in the matter of the difficulty of computing discrete logarithms, since breaking the procedure is equivalent to solving the Diffie-Hellman problem (cf. page 116). Pretty good privacy (PGP), the workhorse known throughout the world for encrypting and signing e-mail and documents whose development goes back essentially to the work of Phil Zimmermann, uses the ElGamal procedure for key management (see [Stal], Section 12.1).

A participant A selects a public and associated private key as follows.

ElGamal key generation

1. A chooses a large prime number p such that p − 1 has a large prime divisor close to (p − 1)/2 (cf. page 328) and a primitive root a of the multiplicative group 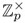as above (cf. page 117).

2. A chooses a random number x with 1 ≤ x < p − 1 and computes b := a^x mod p with the aid of Montgomery exponentiation.

3. As public key A uses the triple <p, a, b>_A, and the associated secret key is <p, a, x>_A.

Using the public key triple <p, a, b>_A a participant B can now encrypt a message M Î {1,...,p − 1 } and send it to A. The procedure is as follows.

Protocol for encryption à la ElGamal

1. B chooses a random number y with 1 ≤ y < p − 1.

2. B calculates α := a^y mod p and β := Mb^y mod p = M (a^x)^y mod p.

3. B sends the cryptogram C := (α, β) to A.

4. A computes from C the plain text using M = β/α^x modulo p.

Since

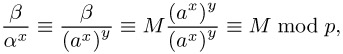
the procedure works. The calculation of β/α^x is carried out by means of a multiplication βα^p−1−x modulo p.

The size of p should be, depending on the application, 1024 bits or longer (see Table 16.1), and for the encryption of different messages M₁ and M₂ unequal random values y₁ ≠ y₂ should be chosen, since otherwise, from

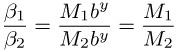
it would follow that knowledge of M₁ was equivalent to knowledge of M₂. In view of the practicability of the procedure one should note that the cryptogram C is twice the size of the plain text M, which means that this procedure has a higher transmission cost than others.

The procedure of ElGamal in the form we have presented has an interesting weak point, which is that an attacker can obtain knowledge of the plain text with a small amount of information. We observe that the cyclic group contains the subgroup U := { a^x | x even} of order (p − 1)/2 (cf. [Fisc], Chapter 1). If now b = a^x or α = a^y lies in U, then this holds, of course, for bα = a^xy. If this is the case and the encrypted text β is also in U, then M = βa^−xy is in U as well. The same holds if a^xy and β are both not contained in U. In the other two cases, in which precisely one of a^xy and β does not lie in U, thenM is also not in U. The following criteria provide information about this situation:

1. a^xy Î U ⇔ (a^x Î U or a^y Î U). This, and whether also β Î U, is tested with

2. For all u Î 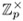, u Î U ⇔ u^(p−1)/2 = 1.

One may ask how bad it might be if an attacker could gain such information about M. From the point of view of cryptography it is a situation difficult to accept, since the message space to be searched is reduced by half with little effort. Whether in practice this is acceptable certainly depends on the application. Surely, it is a valid reason to be generous in choosing the length of a key.

Furthermore, one can take some action against the weakness of the procedure, without, one hopes, introducing new, unknown, weaknesses: The multiplication Mb^y mod p in step 2 of the algorithm can be replaced with an encryption operation V (H (a^xy), M) using a suitable symmetric encryption procedure V (such as Triple-DES, IDEA, or Rijndael, which has become the new advanced encryption standard; cf. Chapter 19) and a hash function H (cf. page 337) that so condenses the value a^xy that it can be used as a key for V.

So much for our examples of the application of modular exponentiation. In number theory, and therefore in cryptography as well, modular exponentiation is a standard operation, and we shall meet it repeatedly later on, in particular in Chapters 10 and 16. Furthermore, refer to the descriptions and numerous applications in [Schr] as well as in the encyclopedic works [Schn] and [MOV].

^[2]IP Security (IPSec), developed by the Internet Engineering Task Force (IETF), is, as an extensive security protocol, a part of the future Internet protocol IPv6. It was created so that it could also be used in the framework of the then current Internet protocol (IPv4). Secure Socket Layer (SSL) is a security protocol developed by Netscape that lies above the TCP protocol, which offers end-to-end security for applications such as HTTP, FTP, and SMTP (for all of this see [Stal], Chapter 13 and14).

^[3]For the problem of calculating discrete logarithms see [Schn], Section 11.6, as well as [Odly].

^[4]ISAKMP: Internet Security Association and Key Management Protocol.

---

Team-Fly