6.3 Addition Chains and Windows

Team-Fly

A number of algorithms for exponentiation have been published, some of which are conceived for special cases and others for general operands. The goal is always to find procedures that employ as few multiplications and divisions as possible, such as in the reduction in the number of operations achieved through passage from binary to M-ary exponentiation.

Binary and M-ary exponentiation are themselves special cases of the construction of addition chains (cf. [Knut], Section 4.6.3). We have already taken advantage of the fact that the laws of exponentiation allow the additive decomposition of the exponent of a power: e = k + l ⇒ a^e = a^k+l = a^k a^l. Binary exponentiation decomposes the exponent into a sum

from which follows the exponentiation in the form of alternating squarings and multiplications (cf. page 80):

The associated addition chain is obtained by considering the exponents to powers of a that arise as intermediate results in this process:

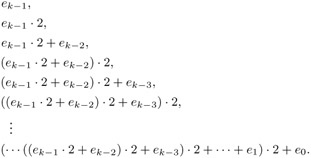
click to expand

Here terms of the sequence are omitted if e_j = 0 for a particular j. For the number 123, for example, based on the binary method the result is the following addition chain with 12 elements: 1, 2, 3, 6, 7, 14, 15, 30, 60, 61, 122, 123.

In general, a sequence of numbers 1 = a₀, a₁, a₂,..., a_r = e for which for every i = 1,...,r there exists a pair (j, k) with j ≤ k < i such that a_i = a_j + a_k holds is called an addition chain for e of length r.

The M-ary method generalizes this principle for the representation of the exponent to other bases. Both methods have the goal of producing addition chains that are as short as possible, in order to minimize the calculational expense for the exponentiation. The addition chain for 123 produced by the 2³-ary method is 1, 2, 3, 4, 7, 8, 15, 30, 60, 120, 123; with the 2⁴-ary method the addition chain 1, 2, 3, 4, 7, 11, 14, 28, 56, 112, 123 is created. These last chains are, as expected, considerably shorter than those obtained by the binary method, which for larger numbers will have a greater effect than in this example. In view of the real savings in time one must, however, note that in the course of initialization for the calculation of a^e mod n the M-ary methods construct the powers a², a³, a⁵, a^M−1 also for those exponents that are not needed in the representation of e to the base M or for the construction of the addition chain.

Binary exponentiation represents the worst case of an addition chain: By considering it we obtain a bound on the greatest possible length of an addition chain of log₂ e + H(e) − 1, where H(e) denotes the Hamming weight of e.^[1] The length of an addition chain is bounded below by log₂ e + log₂ H(e) − 2.13, and so a shorter addition chain for e is not to be found (cf. [Scho] or [Knut], Section 4.6.3, Exercises 28, 29). For our example this means that the shortest addition chain for e = 123 has length at least 8, and so the results of the M-ary methods cited earlier seem not to be the best possible.

The search for shortest addition chains is a problem for which there is as yet no known polynomial-time procedure. It lies in the complexity class NP of those problems that can be solved in polynomial time by nondeterministic methods, that is, those that can be solved by "guessing," in contrast to the class P of problems that can be solved deterministically in polynomial time. It is not surprising that P is a subset of NP, since all polynomial-time deterministic problems can also be solved nondeterministically.

The determination of the shortest addition chain is an NP-complete problem, that is, a problem that is at least as difficult to solve as all other problems in the set NP (cf. [HKW], page 302). The NP-complete problems are therefore of particular interest, since if for even one of them a deterministic polynomial-time procedure could be found, then all other problems in NP could be solved in polynomial time as well. In this case the classes P and NP would collapse into a single set of problems. The unsolved problem of whether P = NP is a central problem of complexity theory. However, as of the present, the betting is in favor of P ≠ NP.

With this it is clear that all practical procedures for generating addition chains must rest on heuristics, that is to say, mathematical rules of thumb such as that for the determination of the exponent k in 2^k-ary exponentiation, of which one knows that it has better time behavior than other methods.

For example, in 1990 Y. Yacobi [Yaco] described a connection between the construction of addition chains and the compression of data according to the Lempel-Ziv procedure; there an exponentiation algorithm based on this compression procedure as well as on the M-ary method is also given.

In the search for the shortest possible addition chains the M-ary exponentiation can be further generalized, which we shall pursue below in greater detail. The window methods represent the exponent not as in the M-ary method by digits to a fixed base M, but by digits of varying binary lengths. Thus, for example, long sequences of binary zeros, called zero windows, can appear as digits of the exponent. If we recall the M-ary algorithm from page 86, it is clear that for a zero window of length l only the l-fold repetition of squaring is required, and the corresponding step is then

Digits different from zero will be treated, depending on the process, either as windows of fixed length or as variable windows with a maximal length. As with the M-ary process, for every nonzero window (in the following called not quite aptly a "1-window") of length t, in addition to the repeated squaring an additional multiplication by a precalculated factor is required, in analogy to the corresponding step of the 2^k-ary procedure:

The number of factors to be precomputed depends on the permitted maximal length of the 1-window. One should note that the 1-windows in the least-significant position always have a 1 and thus are always odd. The factorization of the exponent digit on page 86 into an even and odd factor will thus at first not be needed. On the other hand, in the course of exponentiation the exponent is processed from left to right, which means for the implementation that first the complete decomposition of the exponent must be carried out and stored before the actual exponentiation can take place.

Yet, if we begin the factorization of the exponent at the most-significant digit and travel from left to right, then every 0- or 1-window can be processed immediately, as soon as it is complete. This means, of course, that we will also obtain 1-windows with an even value, but the exponentiation algorithm is prepared for that.

Both directions of decomposition of the exponent into 1-windows with fixed length l follow essentially the same algorithm, which we formulate below for decomposition from right to left.

Decomposition of an integer e into 0-windows and 1-windows having fixed length l

If the least-significant binary digit is equal to 0, then begin a 0-window and go to step 2; otherwise, begin a 1-window and go to step 3.
Add the next-higher binary digits in a 0-window as long as no 1 appears. If a 1 appears, then close the 0-window, begin a 1-window, and go to step 3.
Collect a further l − 1 binary digits into a 1-window. If the next-higher digit is a 0, begin a 0-window and go to step 3; otherwise, begin a 1-window and go to step 3. If in the process all digits of e have been processed, then terminate the algorithm.

The decomposition from left to right begins with the most-significant binary digit and otherwise proceeds analogously. If we suppose that e has no leading binary zeros, then the algorithm cannot reach the end of the representation of e within step 2, and the procedure terminates in step 3 under the same condition given there. The following examples illustrate this process:

Let e = 1896837 = (111001111000110000101)₂, and let l = 3. Beginning with the least-significant binary digit, e is decomposed as follows:

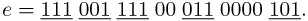
The choice l = 4 leads to the following decomposition of e:

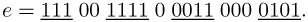
The 2^k-ary exponentiation considered above yields, for example for k = 2, the following decomposition:

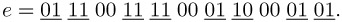
The window decomposition of e for l = 3 contains five 1-windows, while that for l = 4 has only four, and for each the same number of additional multiplications is required. On the other hand, the 2²-ary decomposition of e contains eight 1-windows, requires double the number of additional multiplications compared to the case l = 4, and is thus significantly less favorable.
The same procedure, but beginning with the most-significant binary digit, yields for l = 4 and e = 123 the decomposition

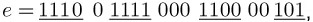
likewise with four 1-windows, which, as already established above, are not all odd.

Finally, then, exponentiation with a window decomposition of the exponent can be formalized by the following algorithm. Both directions of window decomposition are taken into account.

Algorithm for exponentiation a^e mod m with the representation of e in windows of (maximal) length l for odd 1-windows

Decompose the exponent e into 0- and 1-windows (w_k−1...w₀) of respective lengths l_k−1,...,l₀.
Calculate and store a³ mod m, a⁵ mod m, a⁷ mod m,...,a²⁻¹ mod m.
Set p ← 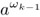mod m and i ← k − 2.
Set p ← 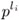mod m.
If w_i ≠ 0, set p ← 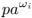mod m.
Set i ← i − 1; if i ≥ 0, go to step 4.
Output p.

If not all 1-windows are odd, then steps 3 through 6 are replaced by the following, and there is no step 7:

3′.	If w_k−1 = 0, set p ← mod m = (l_k−1 times) mod m. If w_k−1 ≠ 0, factor w_k−1 = 2^tu with odd u; set p ← a^u mod m, and then p ← mod m. In each case set i ← k − 2.
4′.	If w_i = 0, set p ← mod m = (l_i times) mod m. If w_i ≠ 0, factor w_i = 2^tu with odd u; set p ← mod m, and then p ← pa^u mod m; now set p ← mod m.
5′.	Set i ← i − 1; if i ≥ 0, go to step 4′.
6′.	Output p.

^[1]If n possesses a representation n = (n_k−1 n_k−2 ... n₀)₂, then H(n) is defined as Σ_i n_i. (See [HeQu], Chapter 8.)

Team-Fly