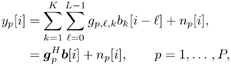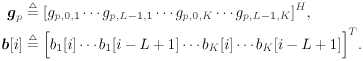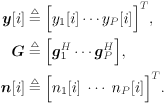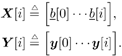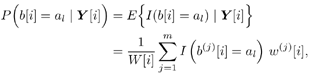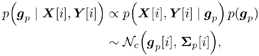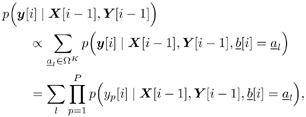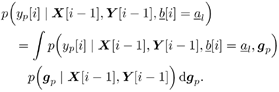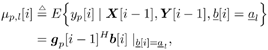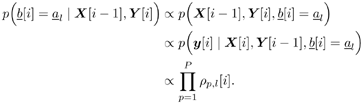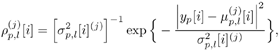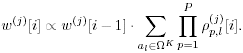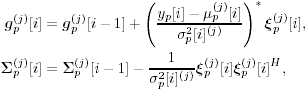8.6 Blind Adaptive Equalization of MIMO Channels via SMC

Many systems can be modeled as multiple-input /multiple-output (MIMO) systems, where the signals observed are superpositions of several linearly distorted signals from different sources. Examples of MIMO systems include space-division multiple access (SDMA) in wireless communications, speech processing, seismic exploration, and some biological systems. The problem of blind source separation for MIMO systems with unknown parameters is of fundamental importance and its solutions find wide applications in many areas. Recently, there has been much interest in solving this problem, and there are primarily two approaches: an approach based on second-order statistics [5, 99, 470, 495], and an approach based on the constant- modulus algorithm [218, 261, 494]. In this section we treat the problem of blind adaptive signal separation in MIMO channels using the SMC method outlined in Section 8.5. The application of SMC technique to blind equalization of single- user ISI channels with single transmit and receive antennas was first treated in [276] and then generalized to multiuser MIMO channels in [543].

8.6.1 System Description

Consider an SDMA communications system with K users. The k th user transmits data symbols { b _k [ i ]} _i in the same frequency band at the same time, where b _k [ i ] W and W is a signal constellation set. The receiver employs an antenna array consisting of P antenna elements. The signal received at the p th antenna element is the superposition of the convolutively distorted signals from all users plus the ambient noise, given by

Equation 8.107

where , L is the length of the channel dispersion in terms of number of symbols, and

Denote

Then (8.107) can be written as

Equation 8.108

We now look at the problem of online estimation of the multiuser symbols

and the channels H based on the received signals up to time i , . Assume that the multiuser symbol streams are i.i.d. uniformly a priori , [i.e., p ( b _k [ i ] = a _l W ) = 1/ W ]. Denote

Then the problem becomes one of making Bayesian inference with respect to the posterior density

Equation 8.109

For example, an online multiuser symbol estimation can be obtained from the marginal posterior distribution and an online channel state estimation can be obtained from the marginal posterior distribution p ( H Y [ i ]). Although the joint distribution (8.109) can be written out explicitly up to a normalizing constant, the computation of the corresponding marginal distributions involves very high dimensional integration and is infeasible in practice. Our approach to this problem is the sequential Monte Carlo technique.

8.6.2 SMC Blind Adaptive Equalizer for MIMO Channels

For simplicity, assume that the noise variance s ² is known. The SMC principle suggests the following basic approach to the blind MIMO signal separation problem discussed above. At time i , draw m random samples,

from some trial distribution q ( ·). Then update the important weights according to (8.97). The a posteriori symbol probability of each user can then be estimated as

Equation 8.110

with

for a _l W , where I ( ·) is an indicator function such that I ( b [ i ] = a _l ) = 1 if b [ i ] = a _l and I ( b [ i ] = a _l ) = 0 otherwise .

Following the discussions above, the trial distribution is chosen to be

Equation 8.111

and the importance weight is updated according to

Equation 8.112

We next specify the computation of the two predictive densities (8.111) and (8.112).

Assume that the channel g _p has an a priori Gaussian distribution:

Equation 8.113

Then the conditional distribution of g _p , conditioned on X [ i ] and Y [ i ] can be computed as

Equation 8.114

where

Equation 8.115

Equation 8.116

Hence the predictive density in (8.112) is given by

Equation 8.117

where

Equation 8.118

Note that the above is an integral of a Gaussian pdf with respect to another Gaussian pdf. The resulting distribution is still Gaussian:

Equation 8.119

with mean and variance given, respectively, by

Equation 8.120

Equation 8.121

Therefore, (8.117) becomes

Equation 8.122

with

Equation 8.123

The filtering density in (8.111) can be computed as follows :

Equation 8.124

Note that the a posteriori mean and covariance of the channel in (8.115) and (8.116) can be updated recursively as follows. At time i , after a new sample of is drawn, we combine it with the past samples b [ i - 1] to form b [ i ]. Let m _p [ i ] and be the quantities computed by (8.120) and (8.121) for the imputed . It then follows from the matrix inversion lemma that (8.115) and (8.116) become

Equation 8.125

Equation 8.126

with

Equation 8.127

Finally, we summarize the SMC-based blind adaptive equalizer in MIMO channels as follows:

Algorithm 8.11: [SMC-based blind adaptive equalizer in MIMO channels]

• Initialization: The initial samples of the channel vectors are drawn from the following a priori distribution :

  

  All importance weights are initialized as , j = 1,..., m . Since the data symbols are assumed to be independent, initial symbols are not needed.

  The following steps are implemented at time i to update each weighted sample. For j = 1,..., m :

• For each and p = 1,..., P , compute the following quantities :

Equation 8.128

Equation 8.129

Equation 8.130

with .

• Impute the multiuser symbol : Draw from the set W ^k with probability

Equation 8.131

• Compute the importance weight :

  

  Let and be the quantities computed in the second step with corresponding to the imputed symbol .

• Update the a posteriori mean and covariance of channels :

  

  with

  

• Do resampling according to Algorithm 8.9 when the effective sample size in (8.103) is below a threshold .

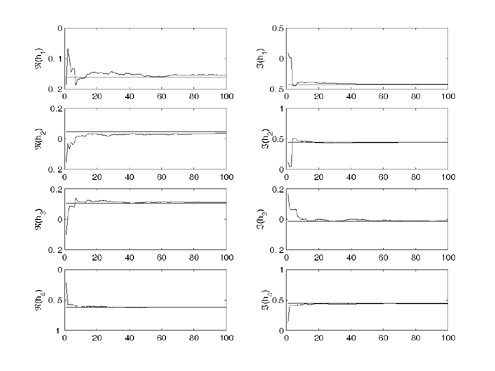
As an example, we consider a single-user system with single transmit and single receive antenna and with channel length L = 4. In Fig. 8.9 we plot the channel estimates as a function of time by the SMC adaptive equalizer. It is seen that the channel can be tracked quickly. Note that, in general, when multiple users and/or multiple antennas are present, there is an ambiguity problem associated with any blind methods , which can be resolved by periodically inserting a certain pattern of pilot symbols. For more discussions on the SMC blind adaptive equalizer, see [276, 277]. Note also that it is possible (and sometimes desirable) to make an inference of the current symbols based on both the current and future observations, Y [ i + D ] for some D > 0 [i.e., to make an inference with respect to p ( Y [ i + D ])] [76, 542]. Called delayed estimation , such approaches are elaborated in Chapter 9. Moreover, when K is large, the choice of sampling density p ( = W ^k ) becomes computationally expensive. It is possible to devise more efficient trial sampling density.

Figure 8.9. Convergence of the SMC blind adaptive equalizer.