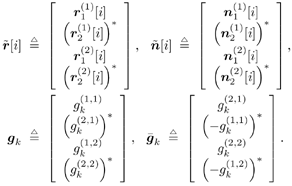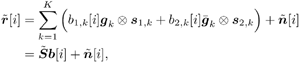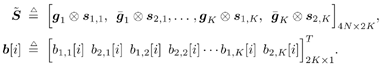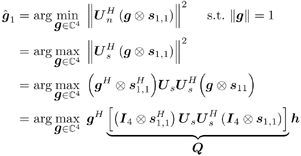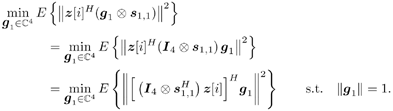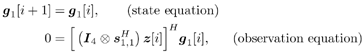5.5 Adaptive Space-Time Multiuser Detection in Synchronous CDMA
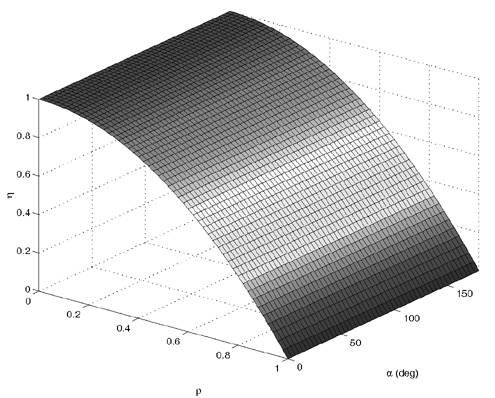
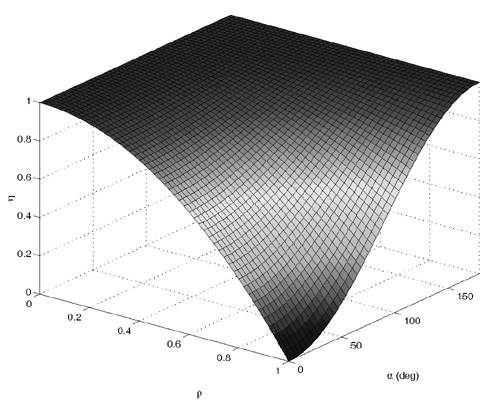
| Generally speaking, space-time processing involves the exploitation of spatial diversity using multiple transmit and/or receive antennas and, perhaps, some form of coding. In previous sections we have focused on systems that employ one transmit antenna and multiple receive antennas. Recently, however, much of the work in this area has focused on transmit diversity schemes that use multiple transmit antennas. They include delay schemes [444, 572, 573] in which copies of the same symbol are transmitted through multiple antennas at different times, the space-time trellis coding algorithm in [477], and the simple space-time block coding (STBC) scheme developed in [12], which has been adopted in third-generation (3G) wideband CDMA (WCDMA) standards [294, 479]. A generalization of this simple space-time block coding concept is developed in [475, 476]. It has been shown that these techniques can significantly increase capacity [122, 478]. In this section we discuss adaptive receiver structures for synchronous CDMA systems with multiple transmit antennas and multiple receive antennas. Specifically, we focus on three configurations: (1) one transmit antenna, two receive antennas; (2) two transmit antennas, one receive antenna; and (3) two transmit antennas, two receive antennas. It is assumed that the orthogonal space-time block code [12] is employed in systems with two transmit antennas. For each of these configurations, we discuss two possible linear receiver structures and compare their performance in terms of diversity gain and signal separation capability. We also describe blind adaptive receiver structures for such multiple-antenna CDMA systems. The methods discussed in this section are generalized in the next section to mutipath CDMA systems. The materials discussed in this and the following sections first appeared in [415]. 5.5.1 One Transmit Antenna, Two Receive AntennasConsider the following discrete-time K - user synchronous CDMA channel with one transmit antenna and two receive antennas. The received baseband signal at the p th antenna can be modeled as Equation 5.95 where s k is the N -vector of the discrete-time signature waveform of the k th user with unit norm (i.e., s k = 1), b k Linear Diversity Multiuser DetectorDenote Suppose that user 1 is the user of interest. We first consider the linear diversity multiuser detection scheme, which first applies a linear multiuser detector to the received signal r p in (5.95) at each antenna p = 1, 2, and then combines the outputs of these linear detectors to make a decision. For example, a linear decorrelating detector for user 1 based on the signal in (5.95) is simply Equation 5.96 where e 1 denotes the first unit vector in Equation 5.97 with Equation 5.98 where w 1 2 = [ R “1 ] 1,1 . Denote Equation 5.99 and Equation 5.100 with Equation 5.101 The maximum- likelihood (ML) decision rule for b 1 based on z in (5.100) is then Equation 5.102 Let Equation 5.103 with Equation 5.104 The probability of detection error is computed as Equation 5.105 Linear Space-Time Multiuser DetectorDenote Then, by augmenting the received signals at two antennas, (5.95) can be written as Equation 5.106 with Equation 5.107 This detector is applied to the augmented received signal Equation 5.108 with Equation 5.109 where Equation 5.110 An expression for Equation 5.111 Equation 5.112 where (5.111) and (5.112) follow, respectively, from the following two matrix identities: Equation 5.113 Equation 5.114 Hence Equation 5.115 where ° denotes the Schur matrix product (i.e., elementwise product). The ML decision rule for b 1 based on Equation 5.116 The probability of detection error is computed as Equation 5.117 Performance ComparisonFrom the discussion above it is seen that the linear space-time multiuser detector exploits the signal structure in both the time domain (i.e., induced by the signature waveform s k ) and the spatial domain (i.e., induced by the channel response g k ) for interference rejection; whereas for the linear diversity multiuser detector, interference rejection is performed only in the time domain, and the spatial domain is used only for diversity combining. The next result, which first appeared in [324], shows that the linear space-time multiuser detector always outperforms the linear diversity multiuser detector. Proposition 5.6: Let Proof: By (5.105) and (5.117) it suffices to show that We make use of the following facts. Denote by A i,j the submatrix of A obtained by striking out the i th row and the j th column. Then it is known that Equation 5.118 It is also known that Equation 5.119 Assuming that Equation 5.120 Equation 5.121 Equation 5.122 where (5.120) follows from the fact that Equation 5.123 and (5.122) follows from Equation 5.124 Hence we have Equation 5.125 We next consider a simple example to demonstrate the performance difference between the two receivers discussed above. Consider a two-user system with where r is the correlation of the signature waveforms of the two users and q 1 and q 2 are the directions of arrival of the two users' signals. Define Equation 5.126 Equation 5.127 Equation 5.128 Equation 5.129 These expressions are plotted in Fig. 5.12. It is seen that while the multiuser space-time receiver can exploit both the temporal signal separation (along the r -axis) and the spatial signal separation (along the a -axis), the multiuser diversity receiver can exploit only the temporal signal separation. For example, for large r , the performance of the multiuser diversity receiver is poor, no matter what value a takes; but the performance of the multiuser space-time receiver can be quite good as long as a is large. Figure 5.12. Performance comparison between a multiuser diversity receiver (top) and multiuser space-time receiver (bottom). 5.5.2 Two Transmit Antennas, One Receive AntennaWhen two antennas are employed at the transmitter, we must first specify how the information bits are transmitted across the two antennas. Here we adopt the well-known orthogonal space-time block coding scheme [12, 475]. Specifically, for user k , two information symbols, b k ,1 and b k ,2 , are transmitted over two symbol intervals. At the first time interval, the symbol pair ( b k ,1 , b k ,2 ) is transmitted across the two transmit antennas; and at the second time interval, the symbol pair ( “ b k ,2 , b k ,1 ) is transmitted. The received signals corresponding to these two time intervals are given by Equation 5.130 Equation 5.131 where g 1, k ( g 2, k ,) is the complex channel response between the first (second) transmit antenna and the receive antenna; n 1 and n 2 are independent received N c ( 0, I N ) noise vectors at the two time intervals. Linear Diversity Multiuser DetectorWe first consider the linear diversity multiuser detection scheme, which first applies the linear multiuser detector w 1 in (5.96) to the received signals r 1 and r 2 during the two time intervals, and then performs a space-time decoding. Specifically, denote Equation 5.132 Equation 5.133 with Equation 5.134 where w 1 2 = [ R “1 ] 1,1 . Denote It is easily seen that Equation 5.135 with Equation 5.136 As before, denote Equation 5.137 The ML decision rule for b 1,1 and b 2,1 based on z in (5.135) is then given by Equation 5.138 Using (5.135), it is easily seen that the decision statistic in (5.138) is distributed according to Equation 5.139 Equation 5.140 Hence the probability of error is given by Equation 5.141 This is the same expression as (5.117) for the linear diversity receiver with one transmit antenna and two receive antennas. Linear Space-Time Multiuser Detector Denote Equation 5.142 On denoting the decorrelating detector for detecting the bit b 1,1 based on Equation 5.143 where Proposition 5.7: The decorrelating detector in (5.143) is given by Equation 5.144 where w 1 is given by (5.96). Proof: We need to verify that Equation 5.145 We have Equation 5.146 Equation 5.147 Equation 5.148 Equation 5.149 This verifies (5.145), so that (5.144) is indeed the decorrelating detector given by (5.143). Thus the output of the linear space-time detector in this case is given by Equation 5.150 with Equation 5.151 where using (5.99) and (5.144), we have Equation 5.152 Therefore, the probability of detection error is given by Equation 5.153 On comparing (5.141) with (5.153) we see that for the case of two transmit antennas and one receive antenna, the linear diversity receiver and the linear space-time receiver have the same performance. Hence the multiple transmit antennas with space-time block coding provide only diversity gain and no signal separation capability. 5.5.3 Two Transmit and Two Receive AntennasWe combine the results from the two preceding sections to investigate an environment in which we use two transmit antennas and two receive antennas. We adopt the space-time block coding scheme used in the preceding section. The received signals at antenna 1 during the two symbol intervals are Equation 5.154 Equation 5.155 and the corresponding signals received at antenna 2 are Equation 5.156 Equation 5.157 where Linear Diversity Multiuser Detector As before, we first consider the linear diversity multiuser detection scheme for user 1, which applies the linear multiuser detector w 1 in (5.96) to each of the four received signals Equation 5.158 Equation 5.159 Equation 5.160 Equation 5.161 with Equation 5.162 where, as before, We define the following quantities : Then (5.158) “(5.162) can be written as Equation 5.163 with Equation 5.164 It is readily verified that Equation 5.165 with Equation 5.166 To form the ML decision statistic, we premultiply z by G 1 and obtain Equation 5.167 with Equation 5.168 The corresponding bit estimates are given by Equation 5.169 The bit error probability is then given by Equation 5.170 Linear Space-Time Multiuser DetectorWe denote Then (5.154) “(5.157) may be written as Equation 5.171 Equation 5.172 where Since Equation 5.173 Hence the output of the linear space-time detector in this case is given by Equation 5.174 with Equation 5.175 where Equation 5.176 Therefore, the probability of detection error is given by Equation 5.177 Comparing (5.177) with (5.170), it is seen that when two transmit antennas and two receive antennas are employed and the signals are transmitted in the form of a space-time block code, the linear diversity receiver and the linear space-time receiver have identical performance. RemarksWe have seen that the performance of space-time multiuser detection (STMUD) and linear diversity multiuser detection (LDMUD) are similar for two transmit/one receive and two transmit/two receive antenna configurations. What, then, are the benefits of the space-time detection technique? They are as follows:
5.5.4 Blind Adaptive Implementations We next develop both batch and sequential blind adaptive implementations of the linear space-time receiver. These implementations are blind in the sense that they require only knowledge of the signature waveform of the user of interest. Instead of the decorrelating detector used in previous sections, we will use a linear MMSE detector for the adaptive implementations because the MMSE detector is more suitable for adaptation and its performance is comparable to that of the decorrelating detector. We consider only the environment in which we have two transmit antennas and two receive antennas. The other cases can be derived in a similar manner. Note that inherent to any blind receiver in multiple transmit antenna systems is an ambiguity issue. That is, if the same spreading waveform is used for a user at both transmit antennas, the blind receiver cannot distinguish which bit is from which antenna. To resolve such an ambiguity, here we use two different spreading waveforms for each user (i.e., s j,k , j There are two bits, b 1, k [ i ] and b 2, k [ i ], associated with each user at each time slot i , and the difference in time between slots is 2 T , where T is the symbol interval. The received signal at antenna 1 during the two symbol periods for time slot i is Equation 5.178 Equation 5.179 and the corresponding signals received at antenna 2 are Equation 5.180 Equation 5.181 We stack these received signal vectors and denote Then we may write Equation 5.182 where The autocorrelation matrix of the stacked signal Equation 5.183 Equation 5.184 where L s = diag { l 1 , l 2 , . . . , l 2 K } contains the largest (2 K ) eigenvalues of C , the columns of U s are the corresponding eigenvectors, and the columns of U n are the 4 N “ 2 K eigenvectors corresponding to the smallest eigenvalue s 2 . The blind linear MMSE detector for detecting [ b [ i ]] 1 = b 1,1 [ i ] is given by the solution to the optimization problem Equation 5.185 From Chapter 2, a scaled version of the solution can be written in terms of the signal subspace components as Equation 5.186 and the decision is made according to Equation 5.187 and Equation 5.188 or Equation 5.189 Before we address specific batch and sequential adaptive algorithms, we note that these algorithms can also be implemented using linear group -blind multiuser detectors instead of blind MMSE detectors. This would be appropriate, for example, in uplink environments in which the base station has knowledge of the signature waveforms of all of the users in the cell, but not those of users outside the cell . Specifically, we may rewrite (5.182) as Equation 5.190 where we have separated the users into two groups. The composite signature sequences of the known users are the columns of Equation 5.191 This detector offers a significant performance improvement over (5.186) for environments in which the signature sequences of some of the interfering users are known. Batch Blind Linear Space-Time Multiuser Detection To obtain an estimate of g 1 , we make use of the orthogonality between the signal and noise subspaces [i.e., the fact that Equation 5.192 Equation 5.193 In (5.193), Algorithm 5.4: [Batch blind linear space-time multiuser detector ”synchronous CDMA, two transmit antennas, and two receive antennas]
A batch group-blind space-time multiuser detector algorithm can be implemented with simple modifications to (5.200) and (5.201). Adaptive Blind Linear Space-Time Multiuser Detection To form a sequential blind adaptive receiver, we need adaptive algorithms for sequentially estimating the channel and the signal subspace components U s and L s . First, we address sequential adaptive channel estimation. Denote by z [ i ] the projection of the stacked signal Equation 5.206 Equation 5.207 Since z [ i ] lies in the noise subspace, it is orthogonal to any signal in the signal subspace, and in particular, it is orthogonal to ( Equation 5.208 To obtain a sequential algorithm to solve the optimization problem above, we write it in the following (trivial) state space form: The standard Kalman filter can then be applied to the system above as follows. Denote Equation 5.209 Equation 5.210 Equation 5.211 Once we have obtained channel estimates at time slot i , we can combine them with estimates of the signal subspace components to form the detector in (5.186). Since we are stacking received signal vectors, and subspace tracking complexity increases at least linearly with signal subspace dimension, it is imperative that we choose an algorithm with minimal complexity. The best existing low-complexity algorithm for this purpose appears to be the NAHJ subspace tracking algorithm discussed in Section 2.6.3. This algorithm has the lowest complexity of any algorithm used for similar purposes and has performed well when used for signal subspace tracking in multipath fading environments. Since the size of U s is 4 N x 2 K , the complexity is 40 · 4 N · 2 K + 3 · 4 N + 7.5(2 K ) 2 + 7 · 2 K floating point operations per iteration. Algorithm 5.5: [Blind adaptive linear space-time multiuser detector ”synchronous CDMA, two transmit antennas, and two receive antennas]
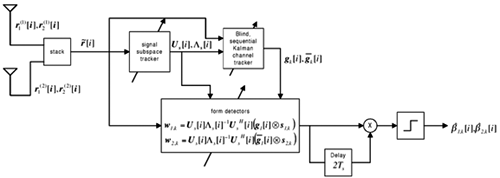
Equation 5.223 Equation 5.224 Equation 5.225 Equation 5.226 A group-blind sequential adaptive space-time multiuser detector can be implemented similarly. The adaptive receiver structure is illustrated in Fig. 5.13. Figure 5.13. Adaptive receiver structure for linear space-time multiuser detectors. |
EAN: 2147483647
Pages: 91
 {+1, “1} is the data bit of the
{+1, “1} is the data bit of the 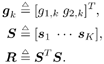
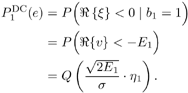
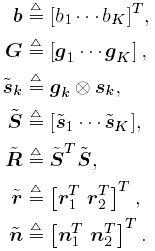
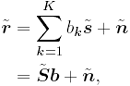
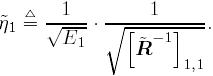
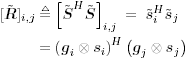
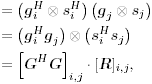
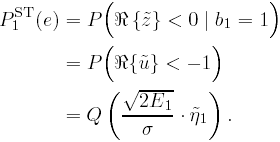
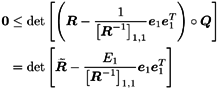
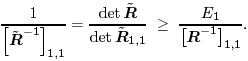
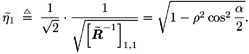
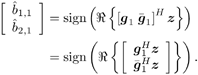
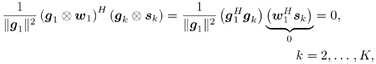
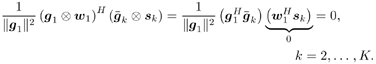
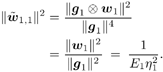
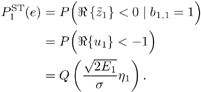
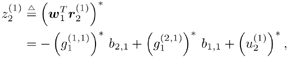
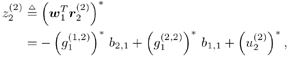
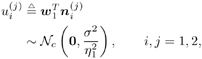
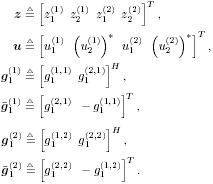
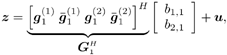
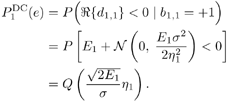
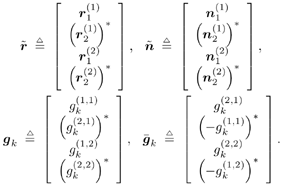
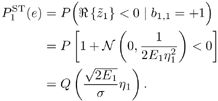
 2 receive antennas.
2 receive antennas.