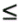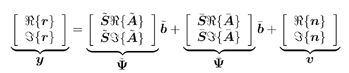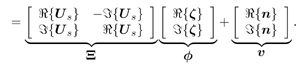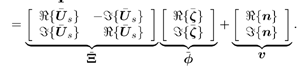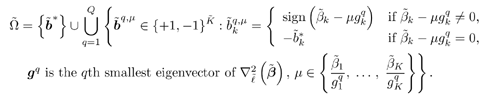4.7 Robust Group -Blind Multiuser Detection Consider the received signal of (4.97). As noted in Chapter 3, in group-blind multiuser detection, only a subset of the K users' signals need to be demodulated. Specifically, suppose that the first  ( (  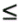 K ) users are the users of interest. Denote K ) users are the users of interest. Denote 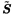 and and 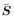 as matrices containing, respectively, the first as matrices containing, respectively, the first 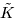 and the last ( K “ and the last ( K “ 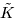 ) columns of S . Similarly define the quantities ) columns of S . Similarly define the quantities 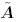 , ,  , , 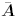 and and 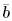 . Then (4.97) can be rewritten as . Then (4.97) can be rewritten as Equation 4.123 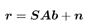
Equation 4.124 
Let the autocorrelation matrix of the received signal and its eigendecomposition be Equation 4.125 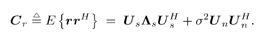
We next consider the problem of nonlinear group-blind multiuser detection in non-Gaussian noise. Denote 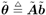 and and  . Then (4.124) can be written as . Then (4.124) can be written as Equation 4.126 
Equation 4.127 
for some 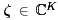 . The basic idea here is to get an estimate of the sum of the undesired users signals, . The basic idea here is to get an estimate of the sum of the undesired users signals, 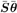 , and to subtract it from r . This effectively reduces the problem to the form treated in Section 4.6. To that end, denote , and to subtract it from r . This effectively reduces the problem to the form treated in Section 4.6. To that end, denote Equation 4.128 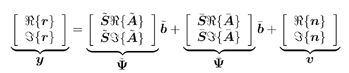
Equation 4.129 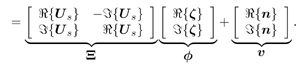
Next, we outline the method for estimating the signal 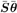 in (4.127). Denote in (4.127). Denote Equation 4.130 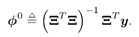
In what follows we assume that the Huber penalty function is used. We first obtain a robust estimate of f by the following iterative procedure: Equation 4.131 
Equation 4.132 
The robust estimate of f translates into a robust estimate of z , which by Proposition 4.2, in turn translates into a robust estimate of 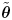 , as , as Equation 4.133 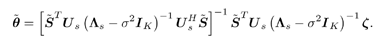
Using the above-estimated 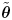 , the desired users' signals are then subtracted from the received signal to obtain , the desired users' signals are then subtracted from the received signal to obtain Equation 4.134 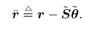
Next, the subspace components of the undesired users' signals are identified as follows. Let Equation 4.135 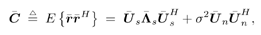
where the dimension of the signal subspace in (4.135) is K “ 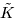 . We then have . We then have Equation 4.136 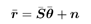
Equation 4.137 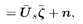
for some 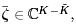 or in its real-valued form, or in its real-valued form, Equation 4.138 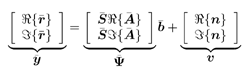
Equation 4.139 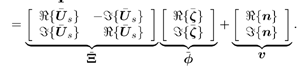
A robust estimate of 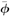 is then obtained from (4.139) using an iterative procedure similar to (4.131)-(4.132). Finally, the estimated undesired users' signals are subtracted from the received signal to obtain is then obtained from (4.139) using an iterative procedure similar to (4.131)-(4.132). Finally, the estimated undesired users' signals are subtracted from the received signal to obtain Equation 4.140 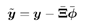
Equation 4.141 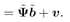
Note that in order to form 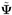 , the complex amplitudes of the desired users, , the complex amplitudes of the desired users, 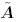 , must be estimated, which can be done based on , must be estimated, which can be done based on 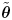 , as discussed in Section 3.4. Note also that such an estimate has a phase ambiguity of p , which necessitates differential encoding and decoding of data. The signal model (4.141) is the same as the one treated in Section 4.6. Accordingly, define the following cost function based on the Huber penalty function: , as discussed in Section 3.4. Note also that such an estimate has a phase ambiguity of p , which necessitates differential encoding and decoding of data. The signal model (4.141) is the same as the one treated in Section 4.6. Accordingly, define the following cost function based on the Huber penalty function: Equation 4.142 
where 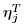 denotes the j th row of the matrix denotes the j th row of the matrix 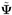 . Let . Let 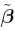 be the stationary point of be the stationary point of 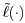 which can also be found using an iterative method similar to (4.105)-(4.106). The Hessian of which can also be found using an iterative method similar to (4.105)-(4.106). The Hessian of 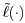 at the stationary point is given by at the stationary point is given by Equation 4.143 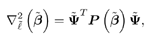
with Equation 4.144 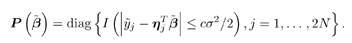
The estimate of the desired users' bits  based on the slowest-descent search is now given by [let based on the slowest-descent search is now given by [let  sign ( sign ( 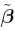 )] )] Equation 4.145 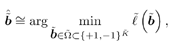
with Equation 4.146 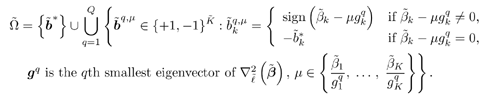
The robust group-blind multiuser detection algorithm for synchronous CDMA with non-Gaussian noise is summarized below. Algorithm 4.5: [Robust group-blind multiuser detector ”synchronous CDMA] -
Compute the sample autocorrelation matrix of the received signal and its eigen-decomposition. -
Compute the robust estimate of f using (4.130)-(4.132); compute the robust estimate of 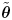 using (4.133). using (4.133). -
Compute the estimate of the complex amplitudes 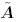 based on the robust estimate of based on the robust estimate of 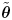 using (3.127)-(3.129) [cf. (3.134)-(3.140)]. using (3.127)-(3.129) [cf. (3.134)-(3.140)]. -
Obtain the robust estimate of the undesired users signals' according to (4.134)-(4.139), by applying an iterative procedure similar to (4.130)-(4.132); subtract the undesired users' signals from the received signal to obtain 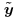 in (4.141). in (4.141). -
Compute the stationary point 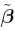 from from 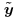 using an iterative procedure similar to (4.105)-(4.106); compute the Hessian using an iterative procedure similar to (4.105)-(4.106); compute the Hessian 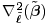 using (4.143) and (4.144). using (4.143) and (4.144). -
Solve the discrete optimization problem defined by (4.145) and (4.146) using an exhaustive search [over ( 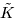 Q + 1) points]; perform differential decoding. Q + 1) points]; perform differential decoding. Simulation Examples We consider a synchronous CDMA system with a processing gain N = 15, the number of users K = 8, and random phase offset and equal amplitudes of user signals. The number of desired users is 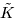 = 4. Only the spreading waveforms = 4. Only the spreading waveforms 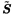 of the desired users are assumed to be known to the receiver. The noise parameters are of the desired users are assumed to be known to the receiver. The noise parameters are 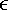 = 0.01, k = 100. The BER curves of the robust blind detector of Section 4.5 (Algorithm 4.2) and the slowest-descent-search robust group-blind detector with Q = 1 and Q = 2 are shown in Fig. 4.13. It is seen that significant performance improvement is offered by the robust group-blind local-search-based multiuser detector in non-Gaussian noise channels over the (nonlinear) blind robust detector discussed in Section 4.5. = 0.01, k = 100. The BER curves of the robust blind detector of Section 4.5 (Algorithm 4.2) and the slowest-descent-search robust group-blind detector with Q = 1 and Q = 2 are shown in Fig. 4.13. It is seen that significant performance improvement is offered by the robust group-blind local-search-based multiuser detector in non-Gaussian noise channels over the (nonlinear) blind robust detector discussed in Section 4.5. Figure 4.13. BER performance of a slowest-descent-based group-blind multiuser detector in non-Gaussian noise: synchronous case. N = 15, K = 8, 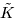 = 4, = 4, 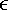 = 0.01, k = 100. = 0.01, k = 100. 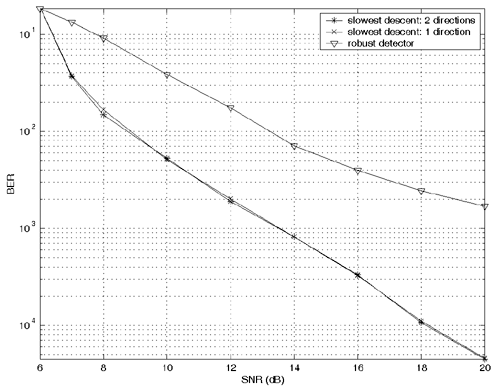 |