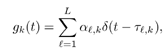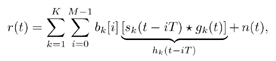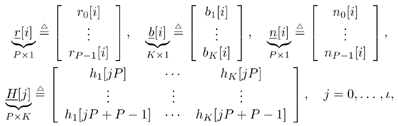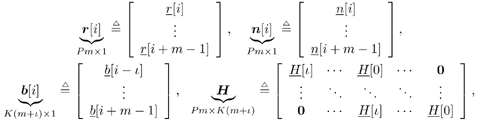| In this section we extend the robust group -blind multiuser detection techniques developed in previous sections to general asynchronous CDMA channels with multipath distortion. Let the impulse response of the k th user 's multipath channel be given by Equation 4.147 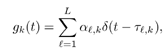
where L is the total number of paths in the channel, and where a l,k and t l,k are, respectively, the complex path gain and the delay of the k th user's l th path. It is assumed that t 1, k < t 2, k < . . . < t L,k . The received continuous-time signal is then given by Equation 4.148 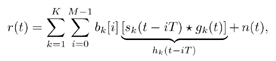
where * denotes convolution. As discussed in Section 2.7.1, at the receiver, the received signal is filtered by a chip-matched filter and sampled at a multiple ( p ) of the chip rate. Denote r q [ i ] as the q th signal sample during the i th symbol [cf. (2.167)]. Recall that by denoting 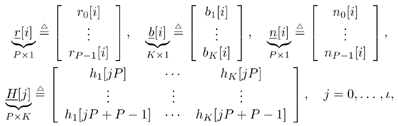 we have the following discrete-time signal model: Equation 4.149 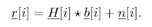
By stacking m successive sample vectors, we further define the following quantities : 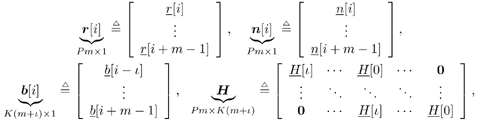 where 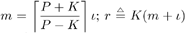 and where l is the maximum delay spread in terms of symbol intervals. We can then have the following matrix form of the discrete-time signal model: and where l is the maximum delay spread in terms of symbol intervals. We can then have the following matrix form of the discrete-time signal model: Equation 4.150 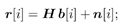
and as before, we write the eigendecomposition of the autocorrelation matrix of the received signal as Equation 4.151 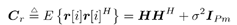
Equation 4.152 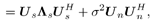
where the signal subspace U s has r columns . We next discuss robust blind multiuser detection and robust group-blind multiuser detection in multipath channels. 4.8.1 Robust Blind Multiuser Detection in Multipath Channels Suppose that user 1 is the user of interest. Then we can rewrite (4.150) as Equation 4.153 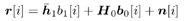
Equation 4.154 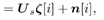
where 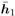 denotes the ( K I + 1)th column of H (corresponding to the bit b 1 [ i ]), H denotes the submatrix of H obtained by striking out the ( K I +1)th column, and b [ i ] denotes the subvector of b [ i ] obtained by striking out the ( K I +1)th element. As before, the basic idea behind robust blind multiuser detection is first to obtain a robust estimate of z [ i ] using the identified signal subspace U s . On the other hand, as discussed in Section 2.7.3, given the spreading waveform s 1 of the desired user, by exploiting the orthogonality between the signal subspace and noise subspace, the composite signature waveform denotes the ( K I + 1)th column of H (corresponding to the bit b 1 [ i ]), H denotes the submatrix of H obtained by striking out the ( K I +1)th column, and b [ i ] denotes the subvector of b [ i ] obtained by striking out the ( K I +1)th element. As before, the basic idea behind robust blind multiuser detection is first to obtain a robust estimate of z [ i ] using the identified signal subspace U s . On the other hand, as discussed in Section 2.7.3, given the spreading waveform s 1 of the desired user, by exploiting the orthogonality between the signal subspace and noise subspace, the composite signature waveform 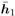 of this user can be estimated (up to a complex scaling factor). Once an estimate of of this user can be estimated (up to a complex scaling factor). Once an estimate of 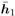 is available, the robust estimate of z [ i ] can then be translated into a robust estimate of b 1 [ i ] (upto a complex scaling factor) by Proposition 4.2, as is available, the robust estimate of z [ i ] can then be translated into a robust estimate of b 1 [ i ] (upto a complex scaling factor) by Proposition 4.2, as Equation 4.155 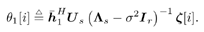
Finally, differential detection is performed according to Equation 4.156 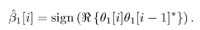
The algorithm is summarized as follows . Algorithm 4.6: [Robust blind multiuser detector ”multipath CDMA] -
Compute the sample autocorrelation matrix of the received augmented signal r [ i ] and its eigendecomposition. -
Compute the robust estimate of z [ i ] following a procedure similar to (4.128)-(4.132). -
Compute an blind estimate of 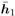 according to (2.202)-(2.203). according to (2.202)-(2.203). -
Compute the output of the robust blind detector according to (4.155). -
Perform differential detection according to (4.156). 4.8.2 Robust Group-Blind Multiuser Detection in Multipath Channels We now turn to the group-blind version of the robust multiuser detector for the multipath channel. As before, we can rewrite (4.150) as Equation 4.157 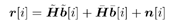
Equation 4.158 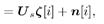
where 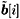 and and 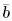 [ i ] contain the data bits in b [ i ] corresponding to sets of desired users and undesired users, respectively; [ i ] contain the data bits in b [ i ] corresponding to sets of desired users and undesired users, respectively; 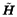 and and 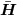 contain columns of H corresponding to desired users and undesired users, respectively. As discussed in Section 2.7.3, based on the knowledge of the spreading waveforms contain columns of H corresponding to desired users and undesired users, respectively. As discussed in Section 2.7.3, based on the knowledge of the spreading waveforms 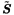 of the desired users, by exploiting the orthogonality between the signal subspace and the noise subspace, we can blindly estimate of the desired users, by exploiting the orthogonality between the signal subspace and the noise subspace, we can blindly estimate 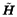 up to a scale and phase ambiguity for each user. With such an estimate, we can write up to a scale and phase ambiguity for each user. With such an estimate, we can write Equation 4.159 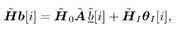
where the term 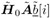 contains the signal carrying the current bits contains the signal carrying the current bits 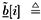 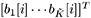 of the desired users; and the term of the desired users; and the term 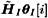 contains the signal carrying the previous and future bits contains the signal carrying the previous and future bits 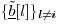 (i.e., the intersymbol interference). Note that in (4.159) the term (i.e., the intersymbol interference). Note that in (4.159) the term 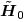 represents the estimated channel for the desired users' current bits, and represents the estimated channel for the desired users' current bits, and 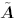 is a diagonal matrix containing the complex scalars of ambiguities ; the term is a diagonal matrix containing the complex scalars of ambiguities ; the term 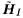 represents the estimated channel for the desired users' past and future bits, and q I [ i ] contains the products of those bits and the complex ambiguities of the corresponding channels. Following the method outlined in Section 4.7, we first obtain a robust estimate of z [ i ] and then translate it into the estimate of represents the estimated channel for the desired users' past and future bits, and q I [ i ] contains the products of those bits and the complex ambiguities of the corresponding channels. Following the method outlined in Section 4.7, we first obtain a robust estimate of z [ i ] and then translate it into the estimate of 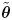 [ i ] by again applying Proposition 4.2: [ i ] by again applying Proposition 4.2: Equation 4.160 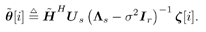
Next, we obtain a robust estimate of the sum of the undesired users' signals based on the relationship Equation 4.161 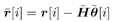
Equation 4.162 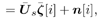
where 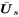 represents the signal subspace obtained from the eigendecomposition of the autocorrelation matrix of represents the signal subspace obtained from the eigendecomposition of the autocorrelation matrix of 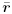 [ i ]. Finally, we subtract the estimated undesired users' signals and the intersymbol interference from r [ i ] to obtain [ i ]. Finally, we subtract the estimated undesired users' signals and the intersymbol interference from r [ i ] to obtain Equation 4.163 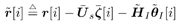
Equation 4.164 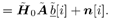
Note that the complex ambiguities in 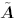 can be estimated based on the estimate of can be estimated based on the estimate of 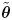 [ i ], as discussed in Section 4.7. Note also that (4.164) has the same form as (4.141), and hence similarly to (4.143) “(4.146), the slowest-descent-search method can then be employed to obtain a robust estimate of [ i ], as discussed in Section 4.7. Note also that (4.164) has the same form as (4.141), and hence similarly to (4.143) “(4.146), the slowest-descent-search method can then be employed to obtain a robust estimate of 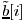 from (4.164). The algorithm is summarized below. from (4.164). The algorithm is summarized below. Algorithm 4.7: [Robust group-blind multiuser detector ”multipath CDMA] -
Compute the sample autocorrelation matrix of the received augmented signal r [ i ] and its eigendecomposition. -
Compute the robust estimate of z [ i ] following a procedure similar to (4.128)-(4.132). -
Compute a blind estimate of 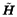 according to (3.162)-(3.163). according to (3.162)-(3.163). -
Compute the output of the robust blind detector according to (4.160). -
Compute the sum of the undesired users' signals 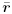 [ i ] according to (4.161); compute the sample autocorrelation matrix of the signal [ i ] according to (4.161); compute the sample autocorrelation matrix of the signal 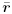 [ i ] and its eigendecomposition. [ i ] and its eigendecomposition. -
Compute the robust estimate of 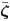 [ i ] in (4.162) following a procedure similar to (4.128)-(4.132). [ i ] in (4.162) following a procedure similar to (4.128)-(4.132). -
Compute the sum of the desired users' signals 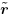 [ i ] according to (4.163). [ i ] according to (4.163). -
Estimate the complex amplitudes of ambiguities 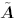 introduced by the blind estimator based on the robust estimate of introduced by the blind estimator based on the robust estimate of 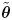 [ i ] using (3.127)-(3.129) [cf. (3.134)-(3.140)]. [ i ] using (3.127)-(3.129) [cf. (3.134)-(3.140)]. -
Form the Huber penalty function and apply the slowest-descent search of 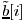 , similar to (4.143) “(4.146). , similar to (4.143) “(4.146). -
Perform differential decoding. Simulation Examples In the following simulation, the number of users is K = 8 and the spreading gain is N = 15. Each user's channel is assumed to have L = 3 paths and a delay spread of up to one symbol. The complex gains and the delays of each user's channel are generated randomly . The chip pulse is a raised cosine pulse with roll-off factor 0.5. The path gains are normalized so that each user's signal arrives at the receiver with unit power. The channel is normalized in such a way that the composite of the multipath channel and the spreading waveform has unit power. The noise parameters are  = 0.01 and k = 100. The smoothing factor is m = 2 and the oversampling factor is p = 2. Shown in Fig. 4.14 is the BER performance of the robust blind multiuser detector and that of the robust group-blind multiuser detector ( = 0.01 and k = 100. The smoothing factor is m = 2 and the oversampling factor is p = 2. Shown in Fig. 4.14 is the BER performance of the robust blind multiuser detector and that of the robust group-blind multiuser detector ( 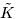 = 4). It is seen that in the presence of both non-Gaussian noise and multipath channel distortion, the group-blind robust detector substantially improves the performance of the blind robust detector. Furthermore, most of the performance gain offered by the slowest-descent search is obtained by searching along only one direction. = 4). It is seen that in the presence of both non-Gaussian noise and multipath channel distortion, the group-blind robust detector substantially improves the performance of the blind robust detector. Furthermore, most of the performance gain offered by the slowest-descent search is obtained by searching along only one direction. Figure 4.14. BER performance of a group-blind robust multiuser detector in non-Gaussian noise: multipath channel. N = 15, K = 8, 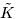 = 4, = 4,  = 0.01, k = 100. Each user's channel consists of three paths with randomly generated complex gains and delays. Only the spreading waveforms = 0.01, k = 100. Each user's channel consists of three paths with randomly generated complex gains and delays. Only the spreading waveforms 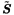 of the desired users are assumed known to the receiver. The BER curves of the robust blind detector (Algorithm 4.2) and robust group-blind detector (Algorithm 4.7) with one and two search directions are shown. of the desired users are assumed known to the receiver. The BER curves of the robust blind detector (Algorithm 4.2) and robust group-blind detector (Algorithm 4.7) with one and two search directions are shown. 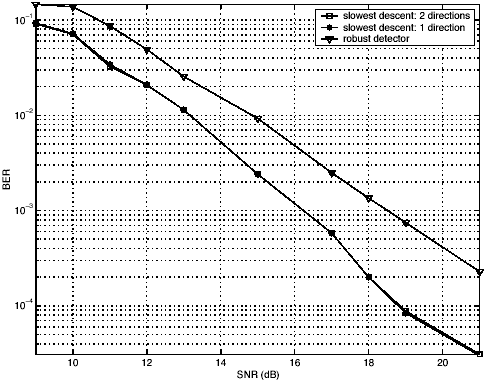  |