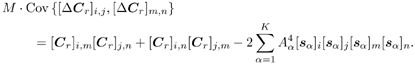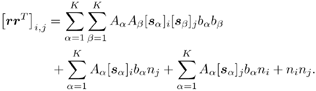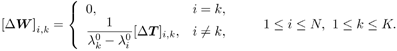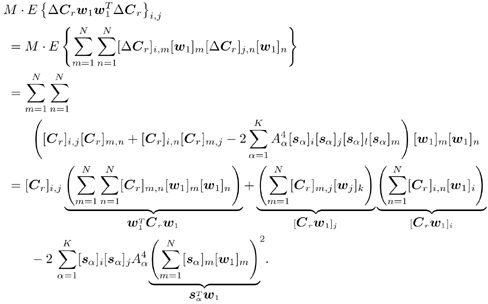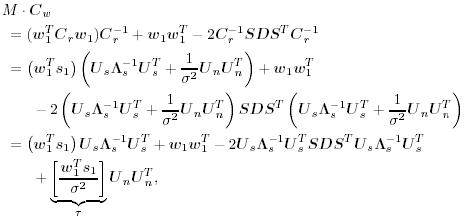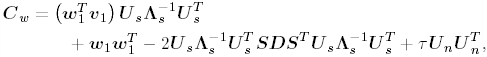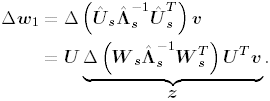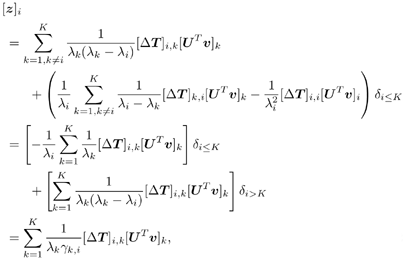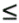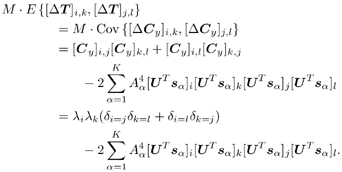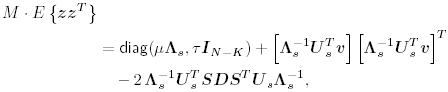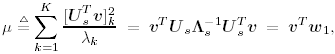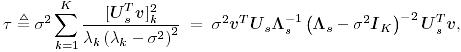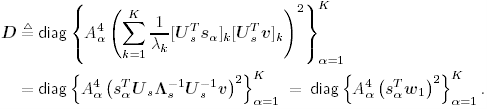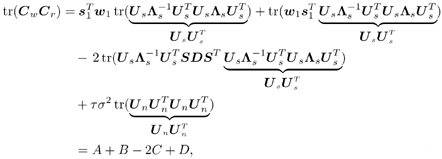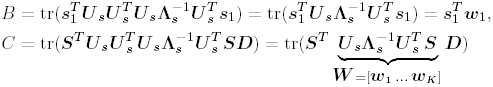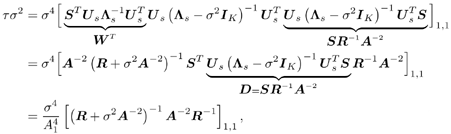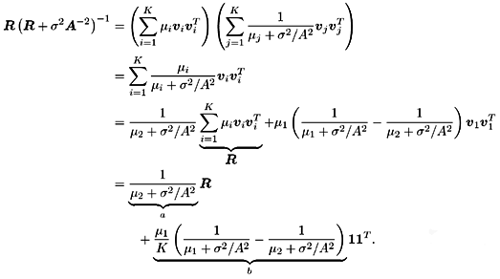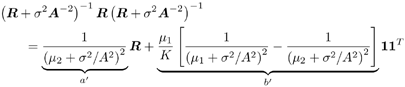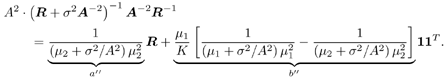2.8 Appendix
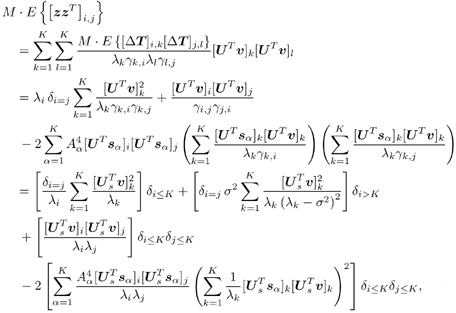
2.8.1 Derivations for Section 2.3.3Derivation of Equation (2.61)Recall that the RLS algorithm for updating the blind linear MMSE algorithm is as follows : Equation 2.247 Equation 2.248 Equation 2.249 Equation 2.250 Equation 2.251 We first derive an explicit recursive relationship between m 1 [ i ] and m 1 [ i -1]. Define Equation 2.252 Premultiplying both sides of (2.249) by Equation 2.253 From (2.253), we obtain Equation 2.254 where Equation 2.255 Substituting (2.249) and (2.254) into (2.250), we get Equation 2.256 where Equation 2.257 is the a priori least-squares estimate at time i . It is shown below that Equation 2.258 Equation 2.259 Substituting (2.248) and (2.258) into (2.256), we get Equation 2.260 Therefore, by (2.260) we have Equation 2.261 where v [ i ] is defined in (2.56). Therefore, from (2.261) we get Equation 2.262 Finally, we derive (2.258) and (2.259). Postmultipling both sides of (2.251) by r [ i ], we get Equation 2.263 On the other hand, (2.247) can be rewritten as Equation 2.264 Equation (2.258) is obtained by comparing (2.263) and (2.264). Multiplying both sides of (2.254) by Equation 2.265 Equation (2.255) can be rewritten as Equation 2.266 Equation (2.259) is obtained comparing (2.265) and (2.266). Derivation of Equations (2.62) “(2.69)Suppose that an application of the rotation matrix Q [ i ] yields the following form: Equation 2.267 Then because of the orthogonality property of Q [ i ] (i.e., Equation 2.268 Equation 2.269 Equation 2.270 Associating A 1 with the first N columns of the partitioned matrix on the left-hand side of (2.62), and B 1 with the first N columns of the partitioned matrix on the right-hand side of (2.62), then (2.268), (2.269), and (2.270) yield Equation 2.271 Equation 2.272 Equation 2.273 Equation 2.274 Equation 2.275 Equation 2.276 A comparison of (2.271) “(2.273) with (2.54) “(2.56) shows that C [ i ], u [ i ], and v [ i ] in (2.62) are the correct updated quantities at time n . Moreover, (2.67) follows from (2.274) and (2.57), (2.68) follows from (2.275) and (2.59), and (2.69) follows from (2.276) and (2.262). 2.8.2 Proofs for Section 2.4.4Proof of Lemma 2.3Denote Note that the eigendecomposition of H is given by Equation 2.277 Then the Moore “Penrose generalized inverse [189] of matrix H is given by Equation 2.278 On the other hand, the Moore “Penrose generalized inverse H Equation 2.279 where the second equality follows from the facts that W T W = I N and S T S Equation 2.280 where in the second equality, the following facts are used: W T W = I N , S T S Equation 2.281 Now (2.107) follows immediately from (2.281) and the fact that U T U = UU T = I N . 2.8.3 Proofs for Section 2.5.2Some Useful LemmasWe first list some lemmas that will be used in proving the results in Section 2.5.2. A random matrix is said to be Gaussian distributed if the joint distribution of all its elements is Gaussian. First we have the following vector form of the central limit theorem. Lemma 2.4: (Theorem 1.9.1B in [443]) Let { x i } be i.i.d. random vectors with mean m and covariance matrix S . Then Next we establish that the sample autocorrelation matrix Lemma 2.5 Denote Equation 2.282 Equation 2.283 Equation 2.284 Then Equation 2.285 Proof: Since Equation 2.286 We have Equation 2.287 where the last equality follows from the fact that Equation 2.288 Note that the last term of (2.285) is due to the nonnormality of the received signal r [ i ]. If the signal had been Gaussian, the result would have been the first two terms of (2.285) only (compare this result with Theorem 3.4.4 in [18]). Using a different modulation scheme (other than BPSK) will result in a different form for the last term in (2.285). In what follows we make frequent use of the differential of a matrix function (cf. [421], Chap. 14). Consider a function Equation 2.289 If the differential exists, it is given by L f ( x ; x ) = T ( x ) x , where Lemma 2.6: (Theorem 3.3A in [443]) Suppose that Let Equation 2.290 where Equation 2.291 Equation 2.292 To calculate C y we can use either (2.291) or (2.292). When dealing with functions of matrices, however, it is usually easier to use (2.292). In what follows we make use of the following identities of matrix differentials: Equation 2.293 Equation 2.294 Equation 2.295 Finally, we have the following lemma regarding the differentials of the eigencomponents of a symmetric matrix. It is a generalization of Theorem 13.5.1 in [18]. Its proof can be found in [197]. Lemma 2.7: Let the N x N symmetric matrix C have an eigendecomposition Equation 2.296 Denote the eigendecomposition of T as Equation 2.297 (Note that if C = C , then W = I N and L = L .) The differential of L at L , and the differential of W at I N , as a function of Equation 2.298 Equation 2.299 Proof of Theorem 2.1 DMI Blind Detector Consider the function Equation 2.300 where
Equation 2.301 Now, by Lemma 2.5, we have Equation 2.302 Writing (2.302) in a matrix form, we have Equation 2.303 with The eigendecomposition of C r is Equation 2.304 Substituting (2.303) and (2.304) into (2.301), we get where the last equality follows from the fact that Subspace Blind Detector We will prove the following more general proposition, which will be used in later proofs. The part of Theorem 2.1 for the subspace blind detector follows with v = s 1 . Proposition 2.6: Let with Equation 2.305 where Equation 2.306 Equation 2.307 Proof: Consider the function Equation 2.308 Since T is a unitary transformation of Equation 2.309 where Equation 2.310 Thus we have Equation 2.311 The differential in (2.311) at ( I N , L ) is given by Equation 2.312 where E s is composed of the first K columns of I N . Using Lemma 2.7, after some manipulations, we have Equation 2.313 with Equation 2.314 where we have used the fact that D T is symmetric (i.e., [ D T ] i,j = [ D T ] j,i ). Denote Equation 2.315 Then C y = U T C r U = L . Moreover, we have D T = D C y . Since E { D T } = , by Lemma 2.5 for 1 Equation 2.316 Using (2.313) and (2.316), we have Equation 2.317 where (2.317) follows from the fact that Equation 2.318 since it is assumed that Equation 2.319 where Equation 2.320 Equation 2.321 Equation 2.322 Finally, by (2.311), Proof of Corollary 2.1 First we compute the term given by (2.120). Using (2.304) and (2.128) and the fact that Equation 2.323 with Equation 2.324 Equation 2.325 Equation 2.326 Equation 2.327 Hence we have Equation 2.328 Next note that the linear MMSE detector can also be written in terms of R as [520] Equation 2.329 Therefore, we have Equation 2.330 Equation 2.331 By (2.130), for the DMI blind detector, we have Equation 2.332 where we have used the fact that the decorrelating detector can be written as [549] Equation 2.333 Finally, substituting (2.328) “(2.332) into (2.119), we obtain (2.132). SINR for Equicorrelated SignalsIn this case, R is given by Equation 2.334 where 1 is an all-1 K -vector. It is straightforward to verify the following eigenstructure of R : Equation 2.335 with Equation 2.336 Equation 2.337 Since A 2 = A 2 I K , we have Equation 2.338 Similarly, we obtain Equation 2.339 Equation 2.340 Substituting (2.338) “(2.340) into (2.132) “(2.135), and defining Equation 2.341 Equation 2.342 Equation 2.343 Equation 2.344 we obtain expression (2.143) for the average output SINRs of the DMI blind detector and the subspace blind detector. |
EAN: 2147483647
Pages: 91
- Structures, Processes and Relational Mechanisms for IT Governance
- Measuring and Managing E-Business Initiatives Through the Balanced Scorecard
- Measuring ROI in E-Commerce Applications: Analysis to Action
- Technical Issues Related to IT Governance Tactics: Product Metrics, Measurements and Process Control
- Governance Structures for IT in the Health Care Industry
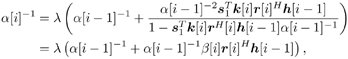
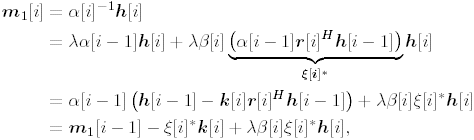
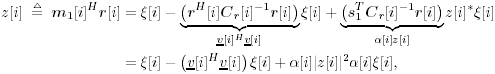
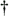 of a matrix
of a matrix 
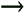
 .
.