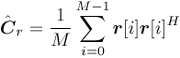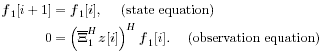2.7 Blind Multiuser Detection in Multipath Channels
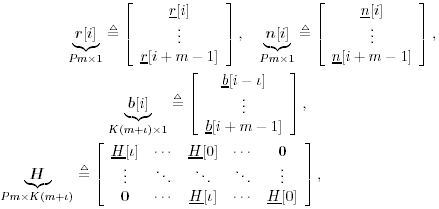
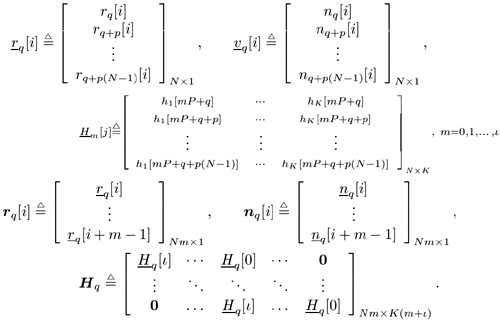
| In previous sections we focused on the synchronous CDMA signal model. In a practical wireless CDMA system, however, the users' signals are asynchronous. Moreover, the physical channel exhibits dispersion due to multipath effects that further distort the signals. In this section we address blind multiuser detection in such channels. As will be seen, the principal techniques developed in previous sections can be applied to this more realistic situation as well. 2.7.1 Multipath Signal ModelWe now consider a more general multiple-access signal model where the users are asynchronous, and the channel exhibits multipath distortion effects. In particular, the multipath channel impulse response of the k th user is modeled as in (1.10): Equation 2.165 where L is the total number of paths in the channel, and a l,k and t l,k are, respectively, the complex path gain and the delay of the k th user's l th path, t 1, k < t 2, k < · · · < t L,k . The continuous-time signal received in this case is given by Equation 2.166 where * denotes convolution and s k (t) is the spreading waveform of the k th user given by (2.2). At the receiver, the received signal r(t) is filtered by a chip-matched filter and sampled at a multiple (p) of the chip rate (i.e., the sampling time interval is D = T c /p = T/P , where be the maximum delay spread in terms of symbol intervals. Substituting (2.2) into (2.166), the q th signal sample during the i th symbol interval is given by! Equation 2.167 where Then (2.167) can be written in terms of vector convolution as Equation 2.168 By stacking m successive sample vectors, we further define the following quantities : where the smoothing factor m is chosen according to Equation 2.169 2.7.2 Linear Multiuser DetectorsSuppose that we are interested in demodulating the data of user 1. Then (2.168) can be written as Equation 2.170 where A linear receiver for this purpose can be represented by a Pm dimensional complex vector Equation 2.171 The coherent detection rule is then given by Equation 2.172 and the differential detection rule is given by Equation 2.173 As before, two forms of such linear detectors are the linear decorrelating detector and the linear minimum mean-square-error (MMSE) detector, which are described next . Linear Decorrelating DetectorThe linear decorrelating detector for user 1 has the form of (2.171) “(2.173) with the weight vector w 1 = d 1 , such that both the multiple-access interference (MAI) and the intersymbol interference (ISI) are eliminated completely at the detector output. [3]
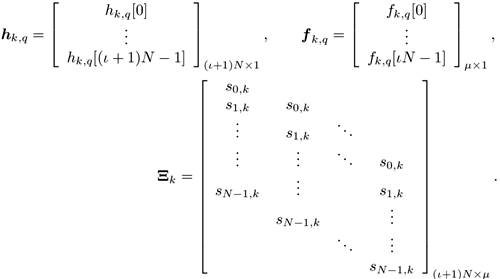
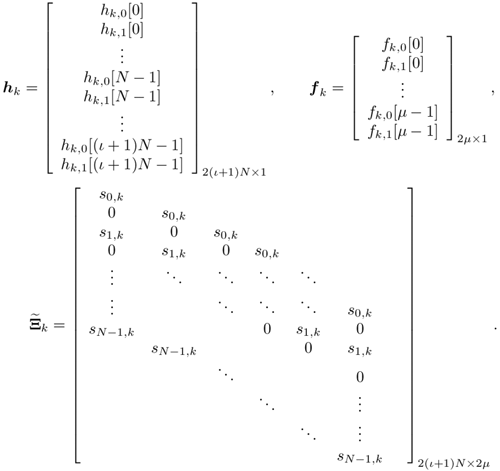
Denote by e l the K ( m + I )-vector with all-zero entries except for the l th entry, which is 1. Recall that the smoothing factor m is chosen such that the matrix H in (2.169) is a tall matrix. Assume that H has full column rank [i.e., Equation 2.174 The linear decorrelating detector for user 1 is then given by Equation 2.175 Using (2.169) and (2.175), we have Equation 2.176 It is seen from (2.176) that both the MAI and the ISI are eliminated completely at the output of the linear zero-forcing detector. In the absence of noise (i.e., n [ i ] = ), the data bit of the desired user, b 1 [ i ], is recovered perfectly . Linear MMSE Detector The linear minimum mean-square-error (MMSE) detector for user 1 has the form of (2.171) “(2.173) with the weight vector w 1 = m 1 , where Equation 2.177 where Equation 2.178 Equation 2.179 Subspace Linear Detectors Let l 1 By performing an eigendecomposition of the matrix C r , we obtain Equation 2.180 where L s = diag ( l 1 , ..., l r ) contains the r largest eigenvalues of C r in descending order, U s = [ u 1 · · · u r ] contains the corresponding orthogonal eigenvectors, and U n = [ u r +1 · · · u Pm ] contains the Pm-r orthogonal eigenvectors that correspond to the eigenvalue s 2 . It is easy to see that range ( H ) = range ( U s ). As before, the column space of U s is called the signal subspace and its orthogonal complement, the noise subspace , is spanned by the columns of U n . Following exactly the same line of development as in the synchronous case, it can be shown that the linear decorrelating detector given by (2.175), and the linear MMSE detector given by (2.177), can be expressed in terms of the signal subspace components above as [548] Equation 2.181 Equation 2.182 Decimation-Combining Linear Detectors The linear detectors discussed above operate in a Pm -dimensional vector space. As will be seen in the next section, the major computation in channel estimation involves computing the singular value decomposition (SVD) of the autocorrelation matrix C r of dimensions Pm x Pm , which has computational complexity For q = 0, ..., p - 1, denote Similar to what we did before, we can write Equation 2.183 Assume that N m Equation 2.184 Equation 2.185 where To detect user 1's data bits, each down-sampled signal vector r q [ i ] is correlated with the corresponding weight vector to obtain Equation 2.186 The data bits are then demodulated according to Equation 2.187 Equation 2.188 In the decimation-combining approach described above, since the signal vectors have dimension Nm , the complexity of estimating each decimated channel response h k,q , q = 0, ..., p “1, is 2.7.3 Blind Channel Estimation It is seen from the discussion above that unlike the synchronous case, where the linear detectors can be written in closed form once the signal subspace components are identified, in multipath channels the composite channel response vector of the desired user, Equation 2.189 with Equation 2.190 where p µ is the length of the channel response { f k [ m ]},which satisfies Equation 2.191 Decimate h k [ n ] into p subsequences as Equation 2.192 Note that the sequences f k,q [ m ] are obtained by down-sampling the sequence { f k [ m ]} by a factor of p : Equation 2.193 From (2.192), we have Equation 2.194 Denote Then (2.194) can be written in matrix form as Equation 2.195 Finally, denote Then we have Equation 2.196 where For other values of p , the matrix Recall that when the ambient channel noise is white, through an eigendecomposition on the autocorrelation matrix of the received signal [cf. (2.180)], the signal subspace and the noise subspace can be identified. The channel response f k can then be estimated by exploiting the orthogonality between the signal subspace and the noise subspace [31, 272, 484, 548]. Specifically, since U n is orthogonal to the column space of H and Equation 2.197 where Equation 2.198 Based on the relationship above, we can obtain an estimate of the channel response f k by computing the minimum eigenvector of the matrix Equation 2.199 That is, Finally, we summarize the batch algorithm for blind linear multiuser detection in multipath CDMA channels as follows . Algorithm 2.7: [Subspace blind linear multiuser detector ”multipath CDMA]
Equation 2.200 Equation 2.201
Equation 2.202 Equation 2.203 Equation 2.204 Equation 2.205
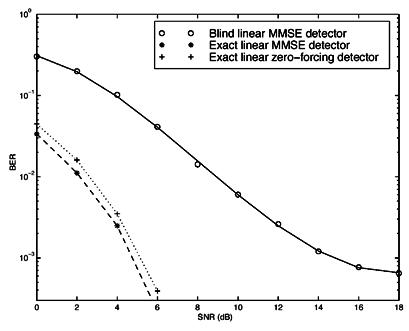
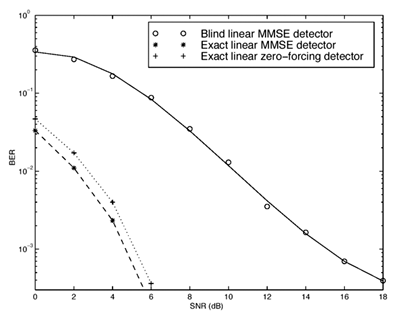
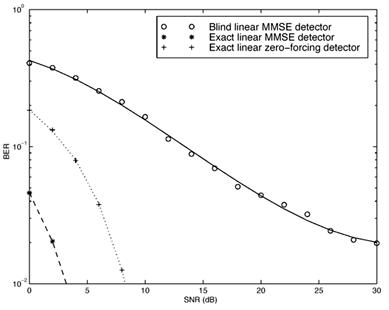
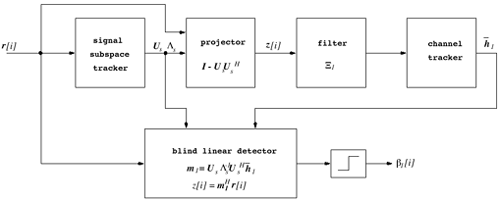
Equation 2.206 Equation 2.207 Alternatively, if the linear receiver has the decimation-combining structure, the noise subspace U n,q is computed for each q = 0, ..., p - 1. The corresponding channel response f k,q can then be estimated from the orthogonality relationship Equation 2.208 Simulation Examples The simulated system is an asynchronous CDMA system with processing gain N = 15. The m -sequences of length 15 and their shifted versions are employed as the user spreading sequences. The chip pulse is a raised cosine pulse with roll-off factor 0.5. Each user's channel has L = 3 paths. The delay of each path t l,k is uniformly distributed on [0, 10 T c ]. Hence the maximum delay spread is one symbol interval (i.e., I = 1). The fading gain of each path in each user's channel is generated from a complex Gaussian distribution and is fixed over the duration of one signal frame. The path gains in each user's channel are normalized so that all users' signals arrive at the receiver with the same power. The oversampling factor is p = 2. The smoothing factor is m = 2. Hence this system can accommodate up to We first consider a five-user system. For the Pm -dimensional implementations , the bit error rates of a particular user incurred by the exact linear MMSE detector, the exact linear zero-forcing detector and the estimated linear MMSE detector are plotted in Fig. 2.13. The bit-error rates of the same user incurred by the three detectors using the decimation-combining structure are plotted in Fig. 2.14. It is seen that for the exact linear zero-forcing and linear MMSE detectors, the performance under the two structures is identical. For the blind linear MMSE receiver, the Pm -dimensional detector achieves an approximately 1-dB performance gain over the decimation-combining detector for SNR in the range 4 to 12 dB. Another observation is that the blind linear MMSE detector tends to exhibit an error floor at high SNR. This is due to the finite length of the signal frame, from which the detector is estimated. Next, a 10-user system is simulated using the Pm -dimensional detectors. The performance of the same user by the three detectors is plotted in Fig. 2.15. Figure 2.13. Performance of Pm -dimensional linear detectors in a five-user system with white noise. Figure 2.14. Performance of decimation-combining linear detectors in a five-user system with white noise. Figure 2.15. Performance of Pm -dimensional linear detectors in a 10-user system with white noise. 2.7.4 Adaptive Receiver StructuresWe next consider adaptive algorithms for sequentially estimating the blind linear detector. First, we address adaptive implementation of the blind channel estimator discussed above. Suppose that the signal subspace U s is known. Denote by z [ i ] the projection of the received signal r [ i ] onto the noise subspace: Equation 2.209 Equation 2.210 Since z [ i ] lies in the noise subspace, it is orthogonal to any signal in the signal subspace. In particular, it is orthogonal to Equation 2.211 In order to obtain a sequential algorithm to solve the optimization problem above, we write it in the following (trivial) state-space form: The standard Kalman filter can then be applied to the system above, as follows (we define Equation 2.212 Equation 2.213 Equation 2.214 Note that (2.213) contains a normalization step to satisfy the constraint f 1 [ i ] = 1. Since the subspace blind detector may be written in closed form as a function of the signal subspace components, one may use a suitable subspace tracking algorithm in conjuction with this detector and a channel estimator to form an adaptive detector that is able to track changes in the number of users and their composite signature waveforms. Figure 2.16 contains a block diagram of such a receiver. The received signal r [ i ] is fed into a subspace tracker that sequentially estimates the signal subspace components ( U s , L s ). The signal r [ i ] is then projected onto the noise subspace to obtain z [ i ], which is in turn passed through a linear filter that is determined by the signature sequence of the desired user. The output of this filter is fed into a channel tracker that estimates the channel state of the desired user. Finally, the linear MMSE detector is constructed in closed form based on the estimated signal subspace components and the channel state. The adaptive receiver algorithm is summarized as follows. Suppose that at time ( i - 1), the estimated signal subspace rank is r [ i - 1] and the components are U s [ i - 1], L s [ i - 1], and s 2 [ i - 1]. The estimated channel vector is f 1 [ i - 1]. Then at time i , the adaptive detector performs the following steps to update the detector and estimate the data. Figure 2.16. Blind adaptive multiuser receiver for multipath CDMA systems. Algorithm 2.8: [Adaptive blind linear multiuser detector based on subspace tracking ”multipath CDMA]
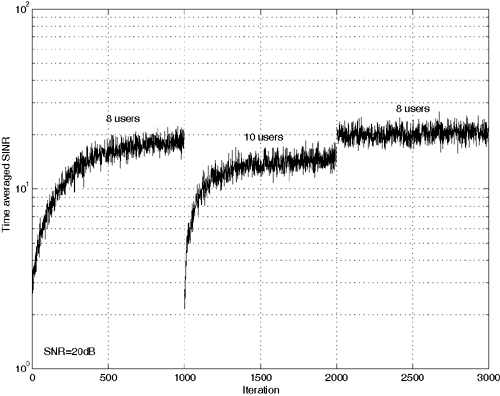
Equation 2.215 Equation 2.216 Equation 2.217 Simulation ExampleWe next give a simulation example illustrating the performance of the blind adaptive receiver in an asynchronous CDMA system with multipath channels. The processing gain N = 15 and the spreading codes are Gold codes of length 15. Each user's channel has L = 3 paths. The delay of each path t l,k is uniformly distributed on [0, 10 T c ]. Hence, as in the preceding example, the maximum delay spread is one symbol interval (i.e., I = 1). The fading gain of each path in each user's channel is generated from a complex Gaussian distribution and is fixed for all simulations. The path gains in each user's channel are normalized so that all users' signals arrive at the receiver with the same power. The smoothing factor is m = 2. The received signal is sampled at twice the chip rate ( p = 2). Hence the total number of users that this system can accommodate is 10. Figure 2.17 shows the performance of subspace blind adaptive receiver using the NAHJ subspace tracking algorithm discussed in Section 2.6.3 in terms of output SINR. During the first 1000 iterations there are eight total users. At iteration 1000, four new users are added to the system. At iteration 2000, one additional known user is added and three existing users vanish . We see that this blind adaptive receiver can closely track the dynamics of the channel. Figure 2.17. Performance of a subspace blind adaptive multiuser detector in an asynchronous CDMA system with multipath. We note that there are many other approaches to blind multiuser detection in multipath CDMA channels, such as constrained optimization methods [59, 60, 80, 187, 300, 305, 306, 427, 485, 487, 490, 498, 583, 584, 605], the auxiliary vector method [364],other subspace methods [10, 31, 252, 258, 272, 287, 446, 484, 548, 551, 564], linear prediction methods [69, 117, 207, 606], the multistage Wiener filtering method [156, 186], the constant modulus method [79, 218, 582], the spreading code design method [435], the maximum- likelihood method [56], the parallel factor method [447], the least-squares smoothing method [483, 610], a method based on cyclostationarity [351], and more general methods based on multiple-input /multiple-output (MIMO) blind channel identification [78, 214, 261, 298, 462, 494 “497]. 2.7.5 Blind Multiuser Detection in Correlated NoiseSo far in developing the subspace-based linear detectors and the channel estimation methods, the ambient channel noise is assumed to be temporally white. In practice, such an assumption may be violated due to, for example, the interference from some narrowband sources. The techniques developed under the white noise assumption are not applicable to channels with correlated ambient noise. In this section we discuss subspace methods for joint suppression of MAI and ISI in multipath CDMA channels with unknown correlated ambient noise, which were first developed in [551]. The key assumption here is that the signal is received by two antennas well separated so that the noise is spatially uncorrelated . We start with the received augmented discrete-time signal model given by (2.169). Assume that the ambient noise vector n [ i ] has a covariance matrix Equation 2.218 The linear MMSE detector m 1 for user 1 is given by (2.177) with C r replaced by (2.218). As before, we must first estimate the desired user's composite signature waveform To estimate the channel in unknown correlated noise, we make use of two antennas at the receiver. Then the two augmented received signal vectors at the two antennas can be written, respectively, as Equation 2.219 Equation 2.220 where H 1 and H 2 contain the channel information corresponding to the respective antennas. It is assumed that the two antennas are well separated so that the ambient noise is spatially uncorrelated . In other words, n 1 [ i ] and n 2 [ i ] are uncorrelated, and their joint covariance is given by Equation 2.221 where S 1 and S 2 are unknown covariance matrices of the noise at the two antennas. The joint autocorrelation matrix of the received signal at the two antennas is then given by Equation 2.222 where the submatrices are given by Equation 2.223 Equation 2.224 Equation 2.225 We next consider two methods for estimating the noise subspaces from the signals received at the two antennas. Singular Value Decomposition Assume that both H 1 and H 2 have full column rank Equation 2.226 The Pm x Pm diagonal matrix G has the form G = diag ( g 1 , ..., g r , 0, ..., 0), with g 1 Equation 2.227 where Equation 2.228 Canonical Correlation DecompositionAssume that the matrices C 11 and C 22 are both positive definite. The canonical correlation decomposition (CCD) of the matrix C 12 is given by [18] Equation 2.229 or Equation 2.230 The Pm x Pm matrix G has the form G = diag ( g 1 , ..., g r , 0, ..., 0), with g 1 Equation 2.231 Partition the matrix L j such that Equation 2.232 where L j,s and L j,n are the first r columns and the last Pm - r columns of L j , respectively. The matrix U j are similarly partitioned into U j,s and U j,n . We have [580]. Equation 2.233 Note, however, that L j,s does not necessarily span the signal subspace range ( H j ) [580]. Now suppose that we have estimated the composite signature waveform of the desired user Equation 2.234 where the second equality in (2.234) follows from (2.231) and the fact that U j is a unitary matrix; and the third equality follows from the fact that Let the estimated weight vectors of the linear MMSE detectors at the two antennas be Equation 2.235 Equation 2.236 We next summarize the procedures for computing the linear MMSE detector Equation 2.237 be the matrix of M received augmented signal sample vectors at antenna j corresponding to one block of data transmission. Algorithm 2.9: [Blind linear MMSE detector in multipath CDMA with correlated noise ”SVD-based method]
Equation 2.238
Equation 2.239
Equation 2.240
Algorithm 2.10: [Blind linear MMSE detector in multipath CDMA with correlated noise ”CCD-based method]
Equation 2.241
Equation 2.242
Equation 2.243
Equation 2.244
Equation 2.245
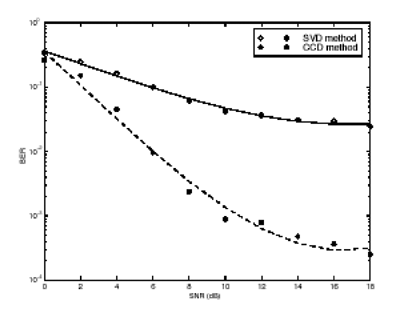
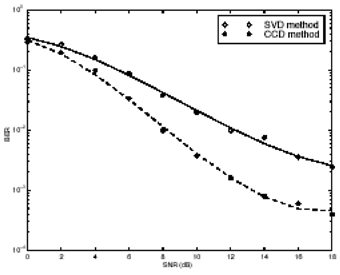
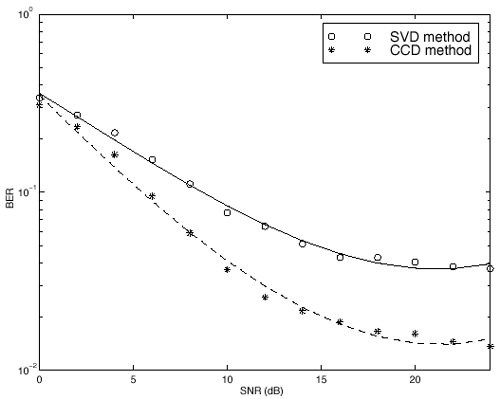
The procedure above is based on the fast algorithm for computing CCD given in [580]. Note that the two methods above operate on the Pm -dimensional signal vectors r j [ i ], j = 1,2. The same procedures can be applied to the decimated received signal vectors to operate on the Nm -dimensional signal vectors r j,q [ i ], j = 1,2, q = 0, ..., p - 1. As before, such decimation-combining approach reduces the computational complexity by a factor of Simulation ExamplesWe illustrate the performance of the detectors above via simulation examples. The simulated system is the same as that in Section 2.7.3, except that the ambient noise is temporally correlated. The noise at each antenna j is modeled by a second-order autoregressive (AR) model with coefficients a j = [ a j ,1 , a j ,2 ]; that is, the noise field is generated according to Equation 2.246 where n j [ i ] is the noise at antenna j and sample i , and w j [ i ] is a complex white Gaussian noise sample with unit variance. The AR coefficients at the two arrays are chosen as a 1 = [1, -0.2] and a 2 = [1.2, -0.3]. We first consider a five-user system. In Fig. 2.18 the performance of the Pm -dimensional blind linear MMSE detectors is plotted for both SVD- and CCD-based methods. The corresponding performance by the decimation-combining receiver structure is plotted in Fig. 2.19. Next a 10-user system is simulated and the performance of the Pm -dimensional blind linear MMSE detectors is plotted in Fig. 2.20. Figure 2.18. Performance of Pm -dimensional blind linear MMSE detectors in a five-user system with correlated noise. Figure 2.19. Performance of decimation-combining blind linear MMSE detectors in a five-user system with correlated noise. Figure 2.20. Performance of Pm -dimensional blind linear MMSE detectors in a 10-user system with correlated noise. It is seen from Figs. 2.18 “2.20 that CCD-based detectors are superior in performance to SVD-based detectors. It has been shown that the CCD has the optimality property of maximizing the correlation between the two sets of linearly transformed data [18]. Maximizing the correlation of the two data sets can yield the best estimate of the correlated (i.e., signal) part of the data. CCD makes use of the information of both |
EAN: 2147483647
Pages: 91
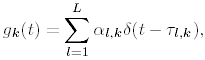
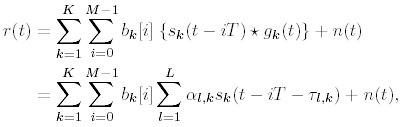

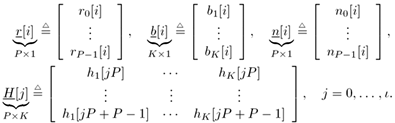
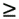 K(m + I )
K(m + I ) 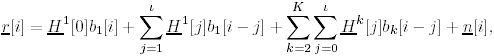
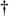 be the Moore “Penrose generalized inverse of the matrix
be the Moore “Penrose generalized inverse of the matrix 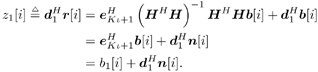
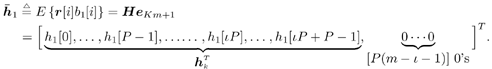
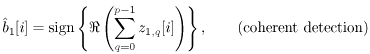
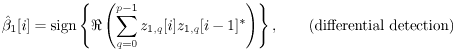
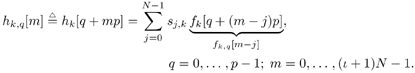
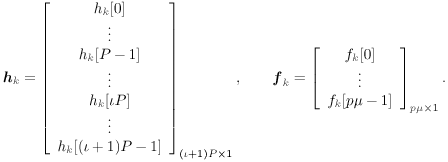
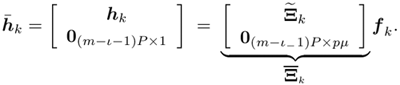
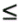 I N
I N