Cryptography: Theory and Practice:Pseudo-random Number Generation

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

THEOREM 12.6

Suppose that algorithm A determines quadratic residuosity correctly with probability at least 1/2 + ε. Then the algorithm A₁, as described in Figure 12.8, is a Monte Carlo algorithm for Quadratic Residues with error probability at most 1/2 + ε.

PROOF For any given input 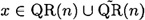, the effect of step 2 in algorithm A₁ is to produce an element x′ that is a random element of 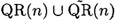whose status as a quadratic residue is known.

The last step is to show that any (unbiased) Monte Carlo algorithm that has error probability at most 1/2 + ε can be used to construct an unbiased Monte Carlo algorithm with error probability at most δ, for any δ > 0. In other words, we can make the probability of correctness arbitrarily close to 1. The idea is to run the given Monte Carlo algorithm 2m + 1 times, for some integer m, and take the “majority vote” as the answer. By computing the error probability of this algorithm, we can also see how m depends on δ. This dependence is stated in the following theorem.

Figure 12.8 A Monte Carlo algorithm for Quadratic Residues

THEOREM 12.7

Suppose A₁ is an unbiased Monte Carlo algorithm with error probability at most 1/2 + ε. Suppose we run A₁ n = 2m + 1 times on a given instance I, and we take the most frequent answer. Then the error probability of the resulting algorithm is at most

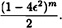
PROOF The probability of obtaining exactly i correct answers in the n trials is at most

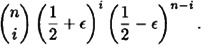
The probability that the most frequent answer is incorrect is equal to the probability that the number of correct answers in the n trials is at most m. Hence, we compute as follows

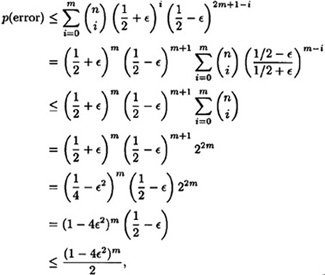
as required.

Suppose we want to lower the probability of error to some value δ, where 0 < δ < 1/2 - ε. We need to choose m so that

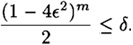
Hence, it suffices to take

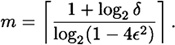
Then, if algorithm A is run 2m + 1 times, the majority vote yields the correct answer with probability at least 1 - δ. It is not hard to show that this value of m is at most c/(δε²) for some constant c. Hence, the number of times that the algorithm must be run is polynomial in 1/δ and 1/ε.

Example 12.5

Suppose we start with a Monte Carlo algorithm that returns the correct answer with probability at least .55, so ε = .05. If we desire a Monte Carlo algorithm in which the probability of error is at most .05, then it suffices to take m = 230 and n = 461.

Let us combine all the reductions we have done. We have the following sequence of implications:

Since it is widely believed that there is no polynomial-time Monte Carlo algorithm for Quadratic Residues with small error probability, we have some evidence that the BBS Generator is secure.

We close this section by mentioning a way of improving the efficiency of the BBS Generator. The sequence of pseudo-random bits is constructed by taking the least significant bit of each s_i, where 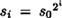mod n. Suppose instead that we extract the m least significant bits from each s_i. This will improve the efficiency of the PRBG by a factor of m, but we need to ask if the PRBG will remain secure. It has been shown that this approach will remain secure provided that m ≤ log₂ log₂ n. So we can extract about log₂ log₂ n pseudo-random bits per modular squaring. In a realistic implementation of the BBS Generator, 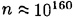, so we can extract nine bits per squaring.

12.4 Probabilistic Encryption

Probabilistic encryption is an idea of Goldwasser and Micali. One motivation is as follows. Suppose we have a public-key cryptosystem, and we wish to encrypt a single bit, i.e., x = 0 or 1. Since anyone can compute e_K (0) and e_K (1), it is a simple matter for an opponent to determine if a ciphertext y is an encryption of 0 or an encryption of 1. More generally, an opponent can always determine if the plaintext has a specified value by encrypting a hypothesized plaintext, hoping to match a given ciphertext.

The goal of probabilistic encryption is that “no information” about the plaintext should be computable from the ciphertext (in polynomial time). This objective can be realized by a public-key cryptosystem in which encryption is probabilistic rather than deterministic. Since there are “many” possible encryptions of each plaintext, it is not feasible to test whether a given ciphertext is an encryption of a particular plaintext.

Here is a formal mathematical definition of this concept.

DEFINITION 12.3 A probabilistic public-key cryptosystem is defined to be a six-tupl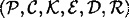e where 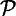is the set of plaintexts, is the set of ciphertexts, 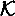is the keyspace, 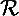is a set of randomizers, and for each key 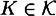, 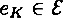is a public encryption rule and 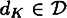is a secret decryption role. The following properties should be satisfied:

1. Each

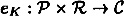and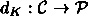

are functions such that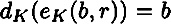

for every plaintext 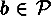and every 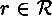. (In particular, this implies that .)

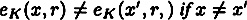2. Let ε be a specified security parameter. For any fixed

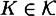and for any

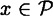, define a probability distribution p_K,x on

, where p_K,x(y) denotes the probability that y is the ciphertext given that K is the key and x is the plaintext (this probability is computed over all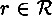

). Suppose

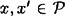, x ≠ x′, and

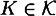. Then the probability distributions p_K,x and p_K,x′ are not ε-distinguishable.

Table of Contents