Cryptography: Theory and Practice:Classical Cryptography | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

DEFINITION 1.3 Suppose a ≥ 1 and m ≥ 2 are integers. If gcd(a, m) = 1, then we say that a and m are relatively prime. The number of integers in 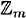that are relatively prime to m is often denoted by φ(m) (function is called the Euler phi-function).

A well-known result from number theory gives the value of φ(m) in terms of the prime power factorization of m. (An integer p > 1 is prime if it has no positive divisors other than 1 and p. Every integer m > 1 can be factored as a product of powers of primes in a unique way. For example, 60 = 2² × 3 × 5 and 98 = 2 × 7².) We record the formula for φ(m) in the following theorem.

THEOREM 1.2

Suppose

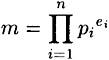
where the p_i′s are distinct primes and e_i > 0, 1 ≤ i ≤ n. Then

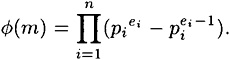
It follows that the number of keys in the Affine Cipher over 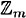is mφ(m), where φ(m) is given by the formula above. (The number of choices for b is m, and the number of choices for a is φ(m), where the encryption function is e(x) = ax + b.) For example, when m = 60, φ(60) = 2 × 2 × 4 = 16 and the number of keys in the Affine Cipher is 960.

Let’s now consider the decryption operation in the Affine Cipher with modulus m = 26. Suppose that gcd(a, 26) = 1. To decrypt, we need to solve the congruence y ≡ ax + b (mod 26) for x. The discussion above establishes that the congruence will have a unique solution in 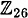, but it does not give us an efficient method of finding the solution. What we require is an efficient algorithm to do this. Fortunately, some further results on modular arithmetic will provide us with the efficient decryption algorithm we seek.

We require the idea of a multiplicative inverse.

DEFINITION 1.4 Suppose 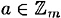. The multiplicative inverse of a is an element 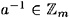such that aa^-1 ≡ a^-1 a ≡ 1 (mod m).

By similar arguments to those used above, it can be shown that a has a multiplicative inverse modulo m if and only if gcd(a, m) = 1; and if a multiplicative inverse exists, it is unique. Also, observe that if b = a^-1, then a = b^-1. If p is prime, then every non-zero element of 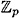has a multiplicative inverse. A ring in which this is true is called a field.

In a later section, we will describe an efficient algorithm for computing multiplicative inverses in 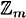for any m. However, in 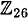, trial and error suffices to find the multiplicative inverses of the elements relatively prime to 26: 1^-1 = 1, 3^-1 = 9, 5^-1 = 21, 7^-1 = 15, 11^-1 = 19, 17^-1 = 23, and 25^-1 = 25. (All of these can be verified easily. For example, 7 × 15 = 105 ≡ 1 mod 26, so 7^-1 = 15.)

Consider our congruence y ≡ ax + b (mod 26). This is equivalent to

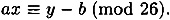
Since gcd(a, 26) = 1, a has a multiplicative inverse modulo 26. Multiplying both sides of the congruence by a^-1, we obtain

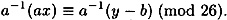
Figure 1.4 Affine Cipher

By associativity of multiplication modulo 26,

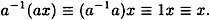
Consequently, x ≡ a^-1(y - b) (mod 26). This is an explicit formula for x, that is, the decryption function is

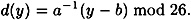
So, finally, the complete description of the Affine Cipher is given in Figure 1.4. Let’s do a small example.

Example 1.3

Suppose that K = (7, 3). As noted above, 7^-1 mod 26 = 15. The encryption function is

and the corresponding decryption function is

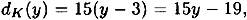
where all operations are performed in 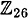. It is good check to verify that d_K(e_K(x)) = x for all 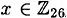Computing in 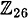, we get

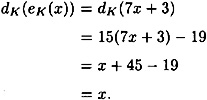
Figure 1.5 Vigenere Cipher

To illustrate, let’s encrypt the plaintext hot. We first convert the letters h, o, t to residues modulo 26. These are respectively 7, 14, and 19. Now, we encrypt:

7 × 7 + 3 mod 26	=	52 mod 26	= 0
7 × 14 + 3 mod 26	=	101 mod 26	= 23
7 × 19 + 3 mod 26	=	136 mod 26	= 6.

So the three ciphertext characters are 0, 23, and 6, which corresponds to the alphabetic string AXG. We leave the decryption as an exercise for the reader.

1.1.4 The Vigenere Cipher

In both the Shift Cipher and the Substitution Cipher, once a key is chosen, each alphabetic character is mapped to a unique alphabetic character. For this reason, these cryptosystems are called monoalphabetic. We now present in Figure 1.5 a cryptosystem which is not monoalphabetic, the well-known Vigenere Cipher. This cipher is named after Blaise de Vigenere, who lived in the sixteenth century.

Using the correspondence A ↔ 0, B ↔ 1, . . ., Z ↔ 25 described earlier, we can associate each key K with an alphabetic string of length m, called a keyword. The Vigenere Cipher encrypts m alphabetic characters at a time: each plaintext element is equivalent to m alphabetic characters.

Let’s do a small example.

Example 1.4

Suppose m = 6 and the keyword is CIPHER. This corresponds to the numerical equivalent K = (2, 8, 15, 7, 4, 17). Suppose the plaintext is the string

                      thiscryptosystemisnotsecure.

We convert the plaintext elements to residues modulo 26, write them in groups of six, and then “add” the keyword modulo 26, as follows:

The alphabetic equivalent of the ciphertext string would thus be:

                      VPXZGIAXIVWPUBTTMJPWIZITWZT.

Table of Contents